【算法每日一练】动态规划，图论（换根dp）会议 ，医院设置

目录

        

题目： 会议

 思路：

题目：医院设置 

思路：

---

        

                

        

题目： 会议

         

 思路：

首先，阅读题目可以看出来，这道题目实际上就是求树的重心。

树的重心：

定义：找到一个点，其所有的子树中最大的子树节点数最少，那么这个点就是这棵树的重心，删去重心后，达到的效果是生成的多棵树尽可能平衡。

举个例子：

我们不妨设置d[i]表示以此点为根的所有点总距离和，cnt[i]表示以此为根的节点数

我们首先知道d[1]=16,cnt[1]=10我们来看d[2]应该怎么求,我们发现相对于d[1]来说，如果设2为最佳点,2,5,6其距离-1，剩下的1,4,3,7,8,9,10到其距离+1。

故：d[2]=d[1] - 3 + 7 =20

其中3是子根2对应的节点数cnt[2]，7是1为子根对应的节点数cnt[1]-cnt[2]

得：d[i]=d[fa]-cnt[i]+(cnt[1]-cnt[i])

那么只需要先dfs求出来d[1]和每个点的cnt[i]。然后就可以进行dp最终求出所有点的d[i]。

#include <bits/stdc++.h>
using namespace std;
const int N=50005;
int minn=0x3f3f3f3f,ans,n,d[N],cnt[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){//一定别走fa回去
	cnt[u]++;//先加上自己
	for(int i=0;i<ve[u].size();i++){
		int v=ve[u][i];
		if(v==fa)continue;
		dfs(v,u,len+1);//先求孩子的cnt，之后求自己cnt
		cnt[u]+=cnt[v];
	}
	d[1]+=len;//最后求d[1]
}
void dp(int u,int fa){
	for(int i=0;i<ve[u].size();i++){
		int v=ve[u][i];
		if(v==fa)continue;
		d[v]=d[u]-2*cnt[v]+cnt[1];
		dp(v,u);//这里对自己进行转移更新，再对孩子的更新
	}
}
int main(){
	cin>>n;int a,b;
	for(int i=1;i<n;i++){
		cin>>a>>b;
		ve[a].push_back(b);
		ve[b].push_back(a);
	}
	dfs(1,0,0);
	dp(1,0);
	for(int i=1;i<=n;i++){
		if(d[i]<minn)
			minn=d[i],ans=i;
	}
	cout<<ans<<" "<<minn;
}

上面我打注释的地方一定要理解 

        

        

题目：医院设置 

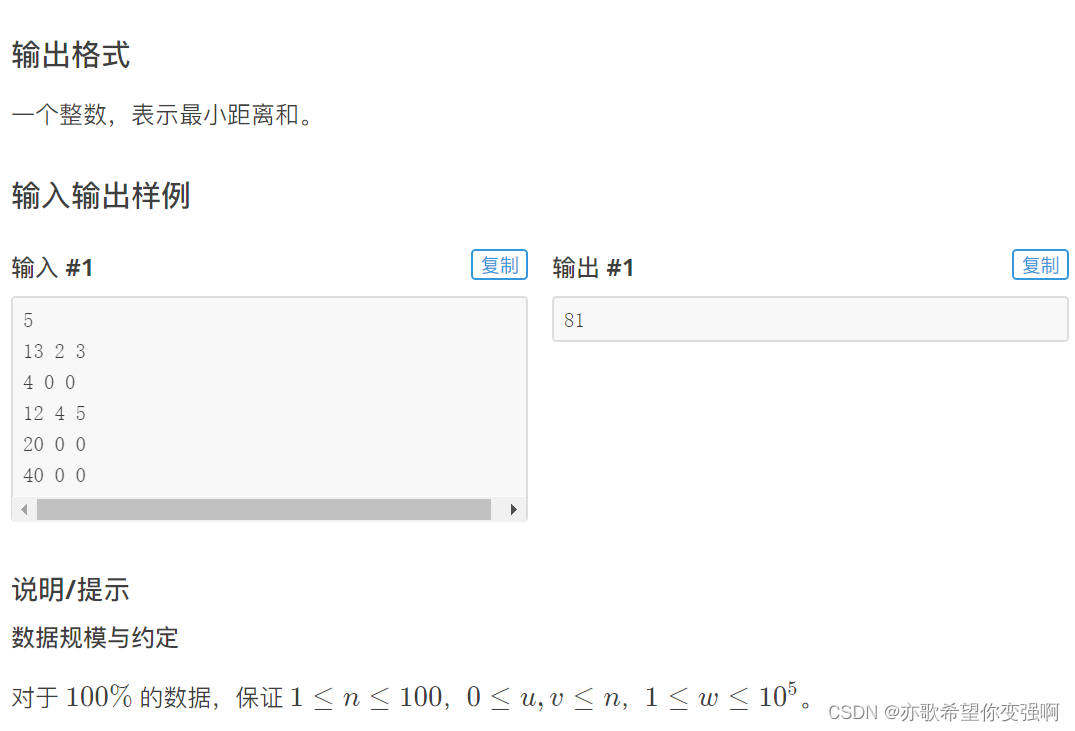
思路：

还是一道求树的重心题。不过是每个点都有一个权值。那么把权值当成“另一个世界的节点数”就好了。然后不断求cnt，之后dp就行。 

#include <bits/stdc++.h>
using namespace std;
const int N=500;
int ans=0x3f3f3f3f,n,d[N],cnt[N],w[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){
	cnt[u]=w[u];//这里还是先加自己
	for(int i=0;i<ve[u].size();i++){
		int v=ve[u][i];
		if(v==fa)continue;
		dfs(v,u,len+1);
		cnt[u]+=cnt[v];
	}
	d[1]+=len*w[u];//更新d[1]也要变一下
}
void dp(int u,int fa){
	for(int i=0;i<ve[u].size();i++){
		int v=ve[u][i];
		if(v==fa)continue;
		d[v]=d[u]+cnt[1]-cnt[v]*2;
		dp(v,u);
	}
	ans=min(ans,d[u]);
}
int main(){
	cin>>n;int c,a,b;
	for(int i=1;i<=n;i++){
		cin>>c>>a>>b;
		w[i]=c;//注意输入方式
		if(a)ve[i].push_back(a),ve[a].push_back(i);
		if(b)ve[i].push_back(b),ve[b].push_back(i);
	}
	dfs(1,0,0);
	dp(1,0);
	cout<<ans;
}