- 1基于Spring Boot的网上商城购物系统设计与实现_spring boot在线购物商城系统实现
- 2Pytorch交叉熵损失函数CrossEntropyLoss及BCE_withlogistic_crossentropy和bce
- 3门控循环单元网络GRU详解_gru 非线性
- 4Github新手使用教程_github下载后怎么使用
- 5运维工程师的出路到底在哪里?—— 浅谈运维工程师前景_运维工程师的前景如何
- 6基于分数阶傅里叶变换和相位分析技术的OFDM雷达距离精度增强_傅里叶变换观察窗
- 7Hadoop HA集群,亲测可用,直接复制粘贴完事_hadoop ha配置
- 8图像 异常检测算法_检测图像异常的算法
- 9JAVA面试题分享四百九十三:Spring Boot与微服务测试:JUnit和Mockito的单元和集成测试实践_java微服务单元测试
- 10华为云创新中心产业开发者高峰论坛圆满举行
二叉树---前,中,后序遍历做题技巧(前,中,后,层次,线索二叉树)_二叉树前中后序遍历做题技巧
赞
踩
目录
1.由二叉树求前,中,后序遍历
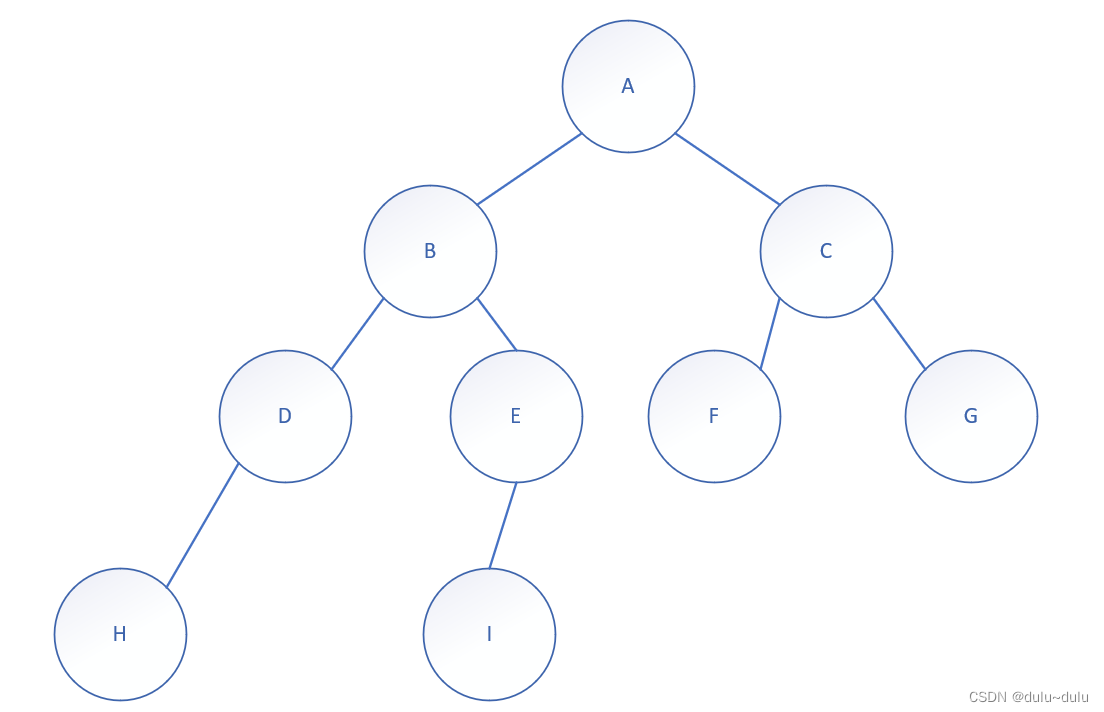
前序:根左右(每一个小方块都遵循)
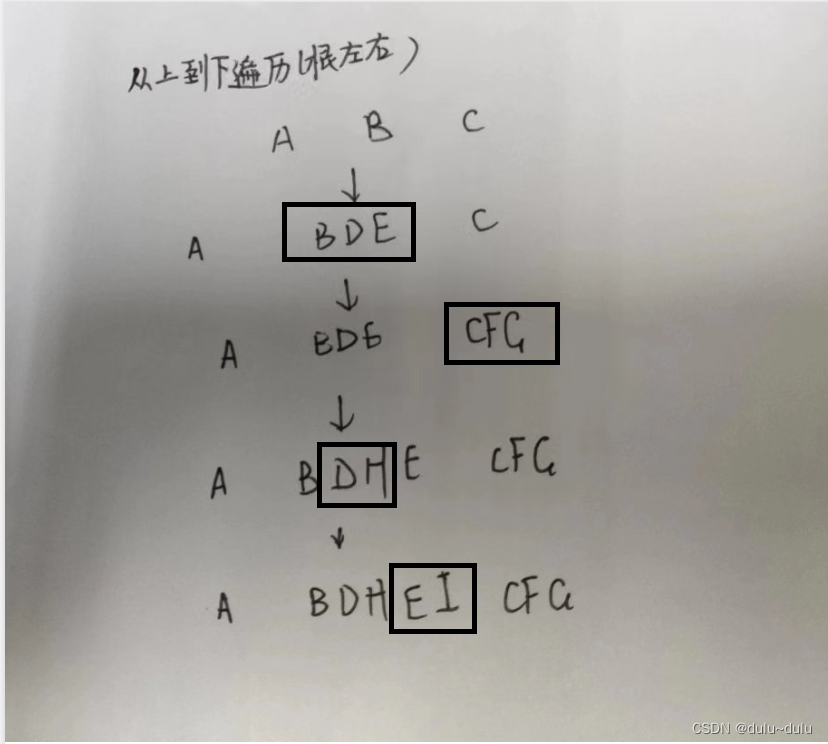
得到:A,B,D,H,E,I,C,F,G
中序:左根右(每一个小方块都遵循)
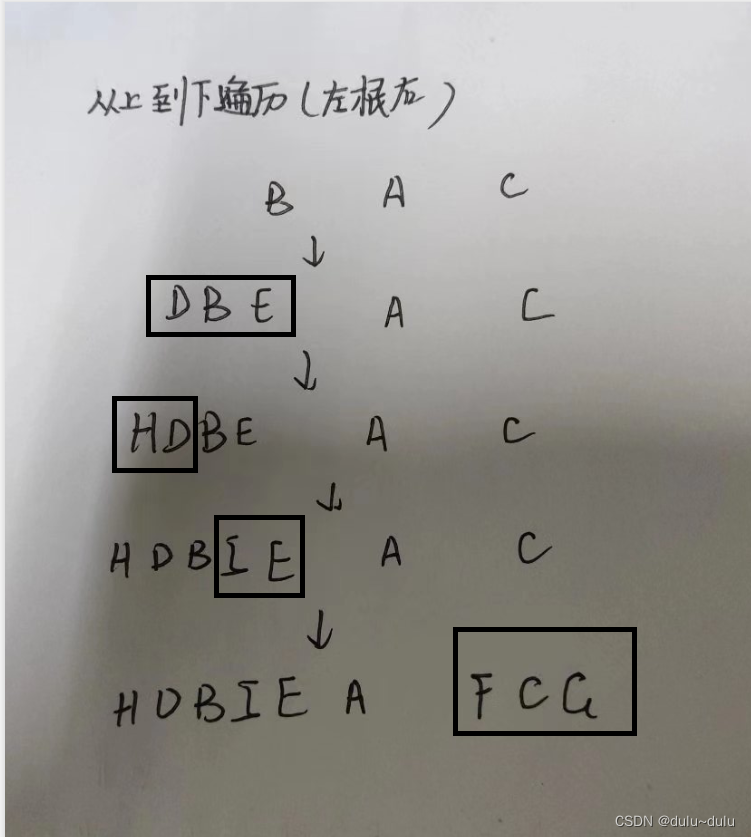
得到:H,D,B,I,E,A,F,C,G
后序:左右根(每一个小方块都遵循)
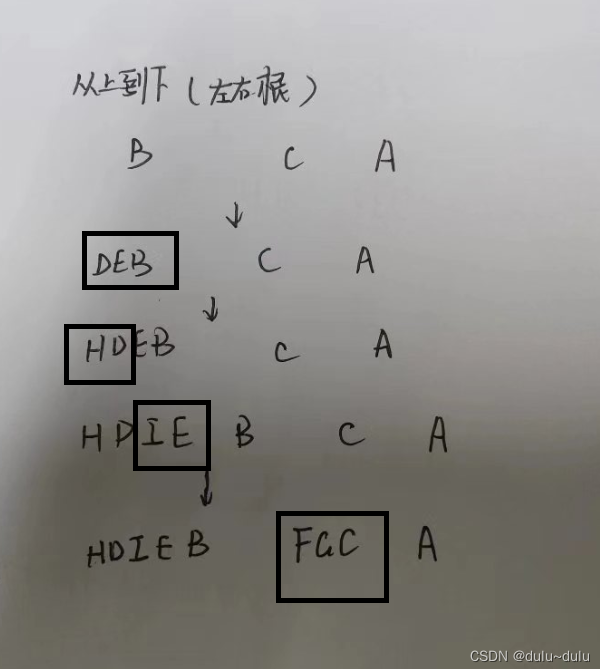
得到:H,D,I,E,B,F,G,C,A
2.由先序,中序或后序,中序得到其余序列
巧妙做法
参考b站“蛮蛮壮”记录的做题技巧
(1).一棵二叉树的先序遍历序列为A,B,C,D,E,F,中序遍历序列为C,B,A,E,D,F,则后序遍历序列为
| A | A | |||||
| B | B | |||||
| C | C | |||||
| D | D | |||||
| E | E | |||||
| F | F | |||||
| C | B | A | E | D | F |
再做如下转换
左子树所有节点在父节点的左边,右子树所有节点在父节点的右边
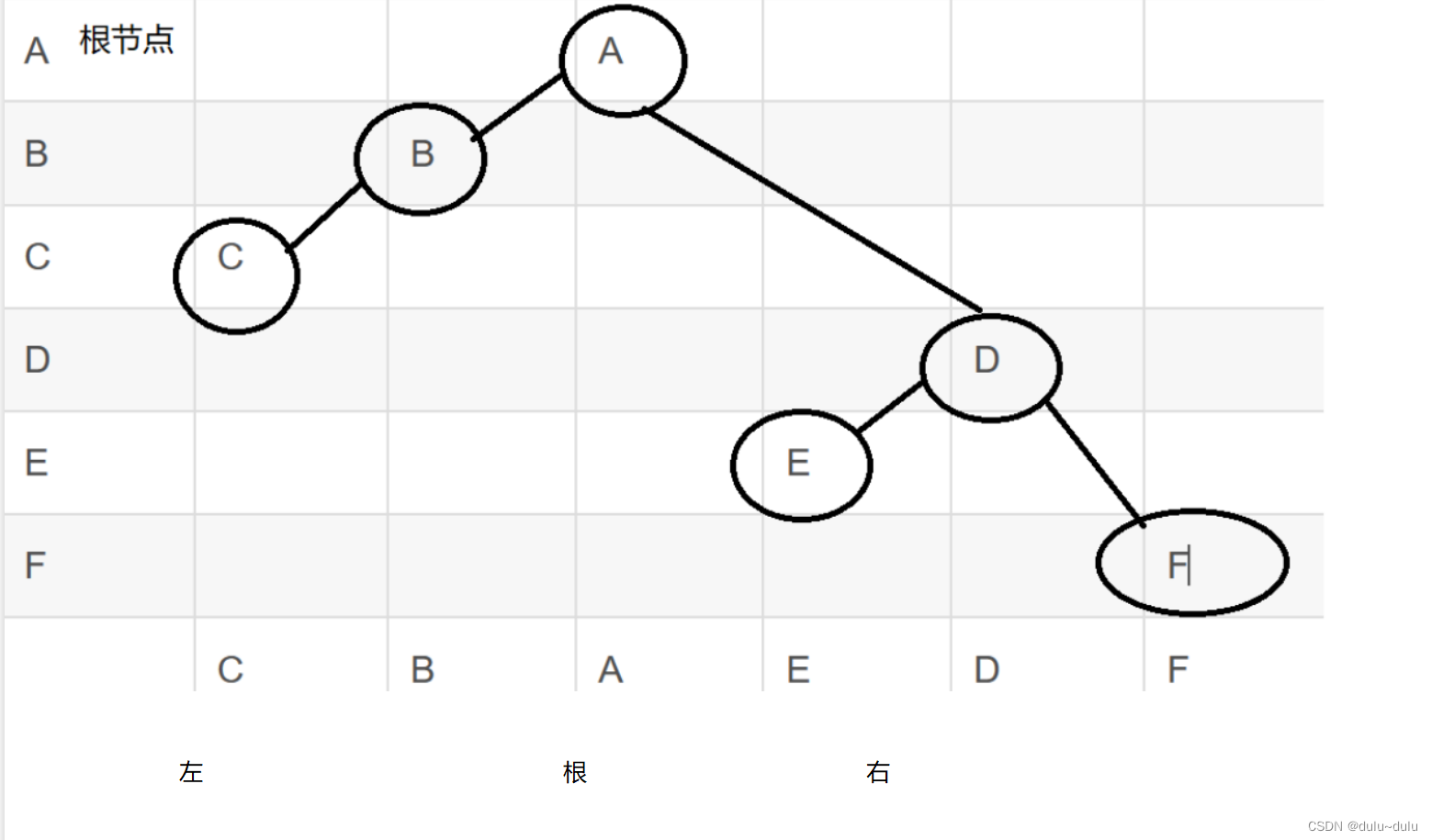
得到后序遍历为C,B,E,F,D,A
(2).一棵二叉树的后序遍历为D,A,B,E,C,中序遍历为D,E,B,A,C,则先序遍历序列为
| C | C | ||||
| E | E | ||||
| B | B | ||||
| A | A | ||||
| D | D | ||||
| D | E | B | A | C |
转换一下
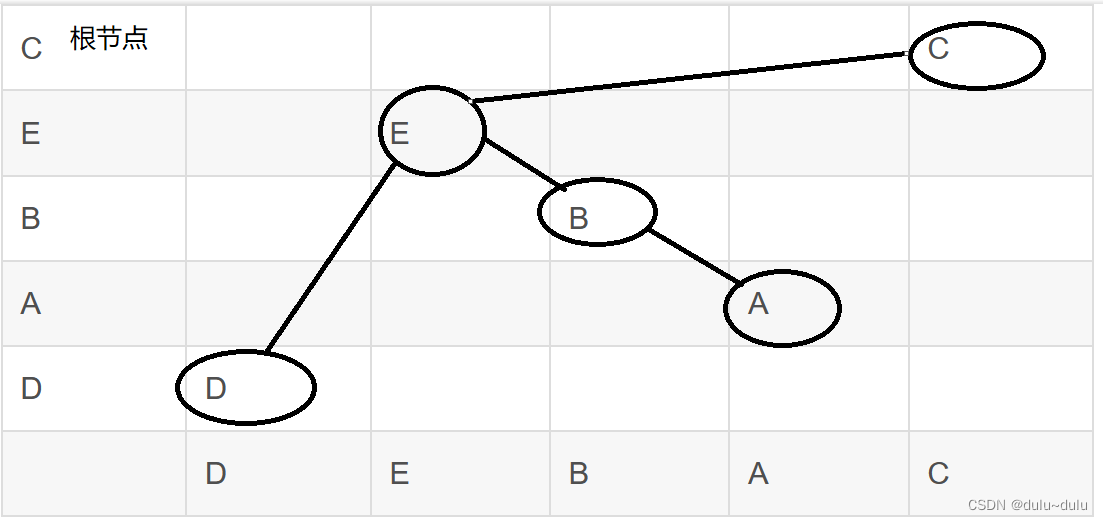
得到先序遍历的结果为:C,E,D,B,A
个人理解
•只有中序和先序或者中序和后序才能确定一个二叉树
•中序遍历是左根右,描述的是一棵树水平节点的顺序,作行,后序遍历和先序遍历可以确定根的位置,将根摆在最上端,而左右就从中序遍历判断
•多做几道题,可以领悟到以下技巧
•父节点在子节点的上方
•左子树所有节点在父节点的左边,右子树所有节点在父节点的右边
常规的做法
前序序列:A,B,D,H,E,C,F
中序遍历:D,H,B,E,A,F,C
•由前序序列知,A是根节点,那么D,H,B,E是左子树,F,C是右子树
•将D,H,B,E带到前序序列中为B,D,H,E,得到B是父节点,同样,将F,C带到前序中为C,F,得到C是父节点
•再将B带到中序遍历中,得到左右子树分别为D,H和E,而C的左子树是F
•D,H再带到前序遍历中,得到D,H,所以父节点是D,至此得到二叉树
总结:
•中序遍历用来确定左右子树
• 前,后序遍历用来确定左右子树的父节点,进而再带到中序序列中划分更小的左右子树

3.层次遍历
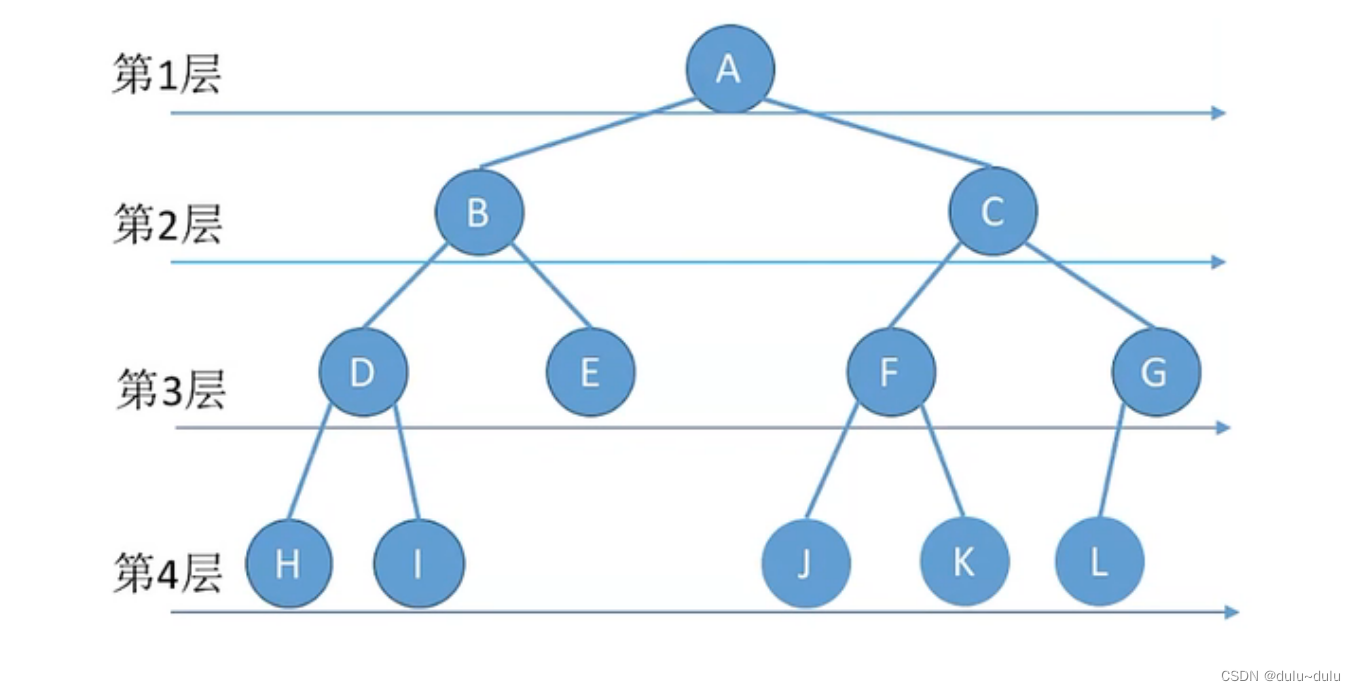
所以层次遍历的结果为A,B,C,D,E,F,G,H,I,J,K,L
4.线索二叉树
如果要找某个节点的前驱和后继,那么必须完整地从根节点开始进行前,中,后遍历
所以线索二叉树可以很直观地看出某个节点的前驱和后继
后序遍历:D,E,B,F,C,A
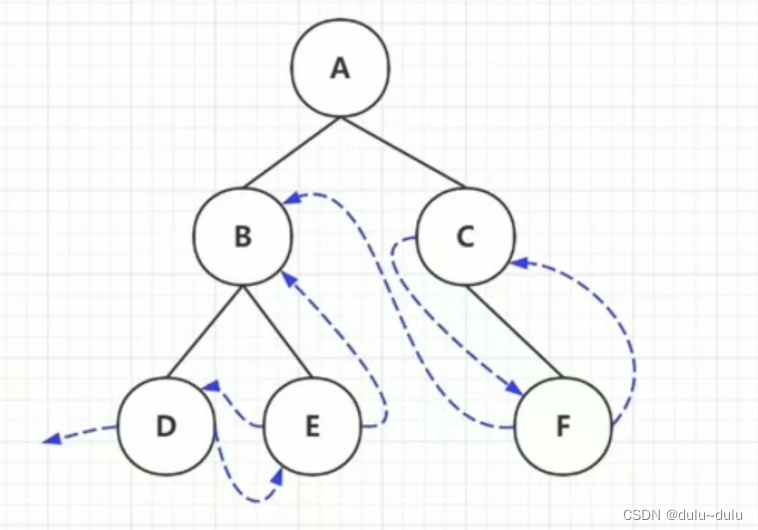
•从上到下,先找只有一个子节点的父节点,如图所示是C
•看线性表D,E,B,F,C,A,C的左侧为F,C指向F
•D没有左右子节点,看线性表D,E,B,F,C,A,D的左侧是空,D的右侧指向E
•以此类推,看E,F,可推出后序线索二叉树
5.树的先根,后跟与层次遍历
以下面的树为例
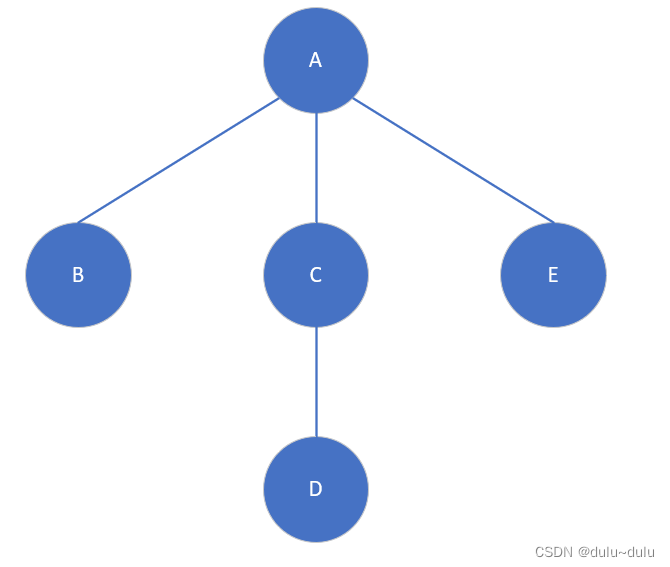
(1)先根遍历
若树不空,则先访问根结点,然后依次先根遍历各棵子树
先根遍历:A,B,C,D,E
(2)后根遍历
若树不空,则先依次后根遍历各各棵子树,然后访问根结点
后根遍历:B,D,C,E,A
(3)按层次遍历
若树不空,则自上而下自左至右访问树中每个结点
层次遍历:A,B,C,E,D
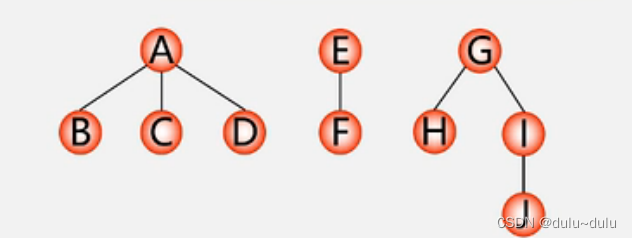
6.森林遍历
(1)森林中第一棵树的根结点
(2)森林中第一棵树的子树森林
(3)森林中其他树构成的森林
•若先遍历第一棵树的根,再遍历第一棵树的子树,最后遍历其他树,则为先序遍历
(依次从左到右对森林中的每一棵树进行先根遍历)
下图先序遍历的结果为:A B C D E F G H I J
•若先遍历第一棵树的子树,再遍历第一棵树的根,最后遍历其他树,则为中序遍历
(依次从左到右对森林中的每一棵树进行后根遍历)
下图中序遍历的结果为:B C D A F E H J I G