Pytorch实现手写数字识别 | MNIST数据集（CNN卷积神经网络）【参考 B站刘二大人】_使用卷积神经网络识别mnist数据集的手写数字

学习的课程： 《PyTorch深度学习实践》完结合集 B站 刘二大人
大佬的专栏笔记： bit452的专栏：PyTorch 深度学习实践
（注：本文承接上文： pytorch实现手写数字识别 | MNIST数据集（全连接神经网络））

CPU版本代码

未下载MNIST数据集的需要将代码中的download=False改为download=True

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# prepare dataset

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])

train_dataset = datasets.MNIST(root='./dataset/mnist/', train=True, download=False, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='./dataset/mnist/', train=False, download=False, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


# design model using class


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)

    def forward(self, x):
        # flatten data from (n,1,28,28) to (n, 784)
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size, -1)  # -1 此处自动算出的是320
        x = self.fc(x)

        return x


model = Net()

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# training cycle forward, backward, update


def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('accuracy on test set: %d %% ' % (100 * correct / total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

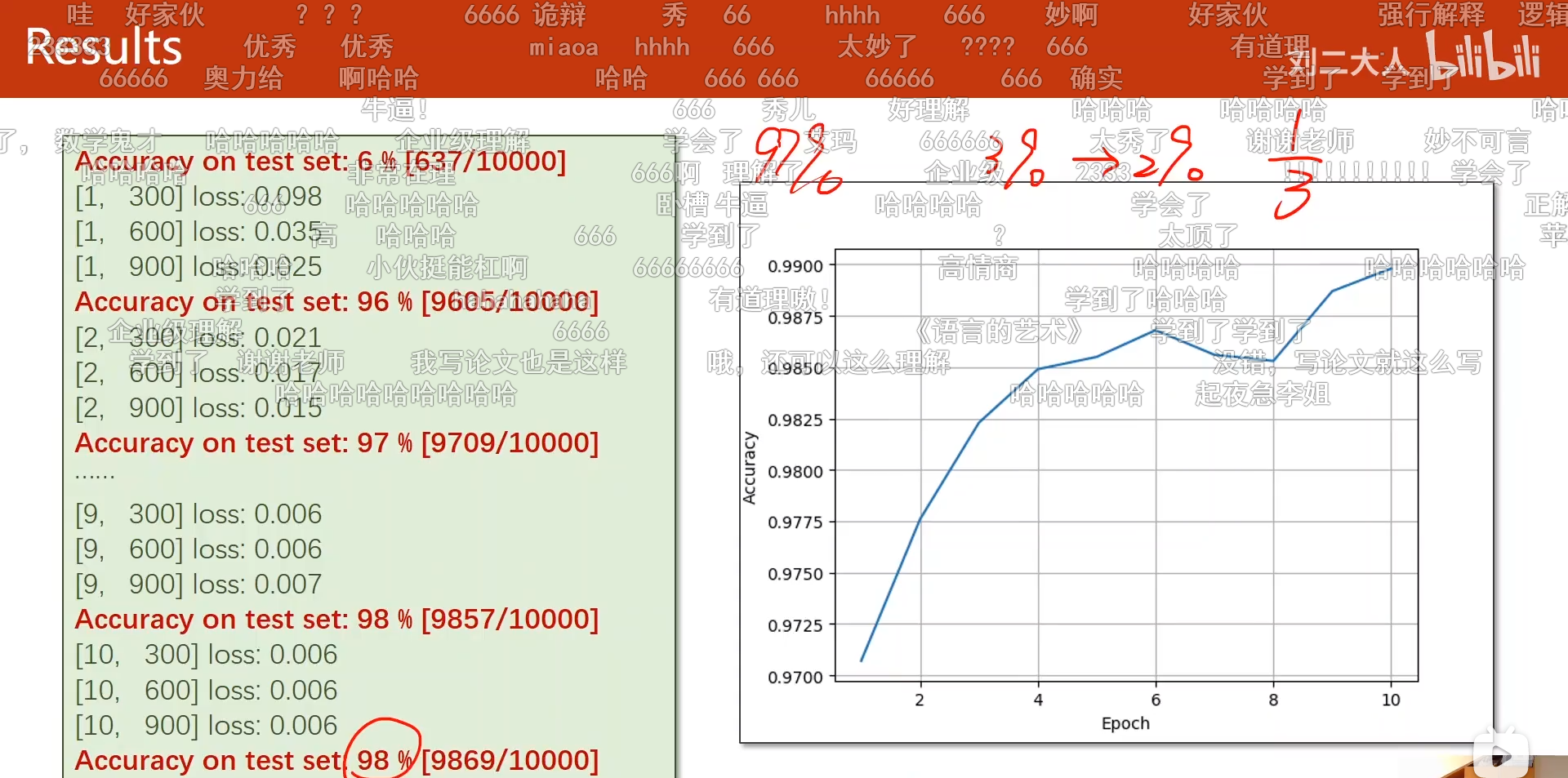
[1,   300] loss: 0.625
[1,   600] loss: 0.181
[1,   900] loss: 0.135
accuracy on test set: 96 % 
[2,   300] loss: 0.111
[2,   600] loss: 0.096
[2,   900] loss: 0.088
accuracy on test set: 97 % 
[3,   300] loss: 0.078
[3,   600] loss: 0.080
[3,   900] loss: 0.073
accuracy on test set: 98 % 
[4,   300] loss: 0.067
[4,   600] loss: 0.061
[4,   900] loss: 0.067
accuracy on test set: 98 % 
[5,   300] loss: 0.055
[5,   600] loss: 0.058
[5,   900] loss: 0.058
accuracy on test set: 98 % 
[6,   300] loss: 0.052
[6,   600] loss: 0.048
[6,   900] loss: 0.053
accuracy on test set: 98 % 
[7,   300] loss: 0.044
[7,   600] loss: 0.050
[7,   900] loss: 0.045
accuracy on test set: 98 % 
[8,   300] loss: 0.041
[8,   600] loss: 0.042
[8,   900] loss: 0.045
accuracy on test set: 98 % 
[9,   300] loss: 0.037
[9,   600] loss: 0.042
[9,   900] loss: 0.041
accuracy on test set: 98 % 
[10,   300] loss: 0.036
[10,   600] loss: 0.036
[10,   900] loss: 0.038
accuracy on test set: 98 % 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

GPU版本代码

未下载MNIST数据集的需要将代码中的download=False改为download=True

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt

# prepare dataset

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])

train_dataset = datasets.MNIST(root='./dataset/mnist/', train=True, download=False, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='./dataset/mnist/', train=False, download=False, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


# design model using class


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)

    def forward(self, x):
        # flatten data from (n,1,28,28) to (n, 784)

        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size, -1)  # -1 此处自动算出的是320
        # print("x.shape",x.shape)
        x = self.fc(x)

        return x


model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)


# training cycle forward, backward, update


def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        inputs, target = inputs.to(device), target.to(device)
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('accuracy on test set: %d %% ' % (100 * correct / total))
    return correct / total


if __name__ == '__main__':
    epoch_list = []
    acc_list = []

    for epoch in range(10):
        train(epoch)
        acc = test()
        epoch_list.append(epoch)
        acc_list.append(acc)

    plt.plot(epoch_list, acc_list)
    plt.ylabel('accuracy')
    plt.xlabel('epoch')
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

[1,   300] loss: 0.698
[1,   600] loss: 0.198
[1,   900] loss: 0.145
accuracy on test set: 96 % 
[2,   300] loss: 0.107
[2,   600] loss: 0.098
[2,   900] loss: 0.089
accuracy on test set: 97 % 
[3,   300] loss: 0.078
[3,   600] loss: 0.070
[3,   900] loss: 0.072
accuracy on test set: 98 % 
[4,   300] loss: 0.066
[4,   600] loss: 0.059
[4,   900] loss: 0.057
accuracy on test set: 98 % 
[5,   300] loss: 0.048
[5,   600] loss: 0.055
[5,   900] loss: 0.056
accuracy on test set: 98 % 
[6,   300] loss: 0.052
[6,   600] loss: 0.044
[6,   900] loss: 0.047
accuracy on test set: 98 % 
[7,   300] loss: 0.042
[7,   600] loss: 0.044
[7,   900] loss: 0.043
accuracy on test set: 98 % 
[8,   300] loss: 0.042
[8,   600] loss: 0.036
[8,   900] loss: 0.042
accuracy on test set: 98 % 
[9,   300] loss: 0.035
[9,   600] loss: 0.038
[9,   900] loss: 0.037
accuracy on test set: 98 % 
[10,   300] loss: 0.035
[10,   600] loss: 0.036
[10,   900] loss: 0.032
accuracy on test set: 98 % 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

相关说明：

1. 卷积神经网络的主要组成

卷积神经网络（Convolutional Neural Networks, CNN）

• 卷积层(Convolutional layer)，卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。

• 池化层(Pooling)，它实际上一种形式的向下采样。有多种不同形式的非线性池化函数，而其中最大池化(Max pooling)和平均采样是最为常见的。（Pooling层相当于把一张分辨率较高的图片转化为分辨率较低的图片；pooling层可进一步缩小最后全连接层中节点的个数，从而达到减少整个神经网络中参数的目的。）

• 全连接层(Full connection), 与普通神经网络一样的连接方式，一般都在最后几层

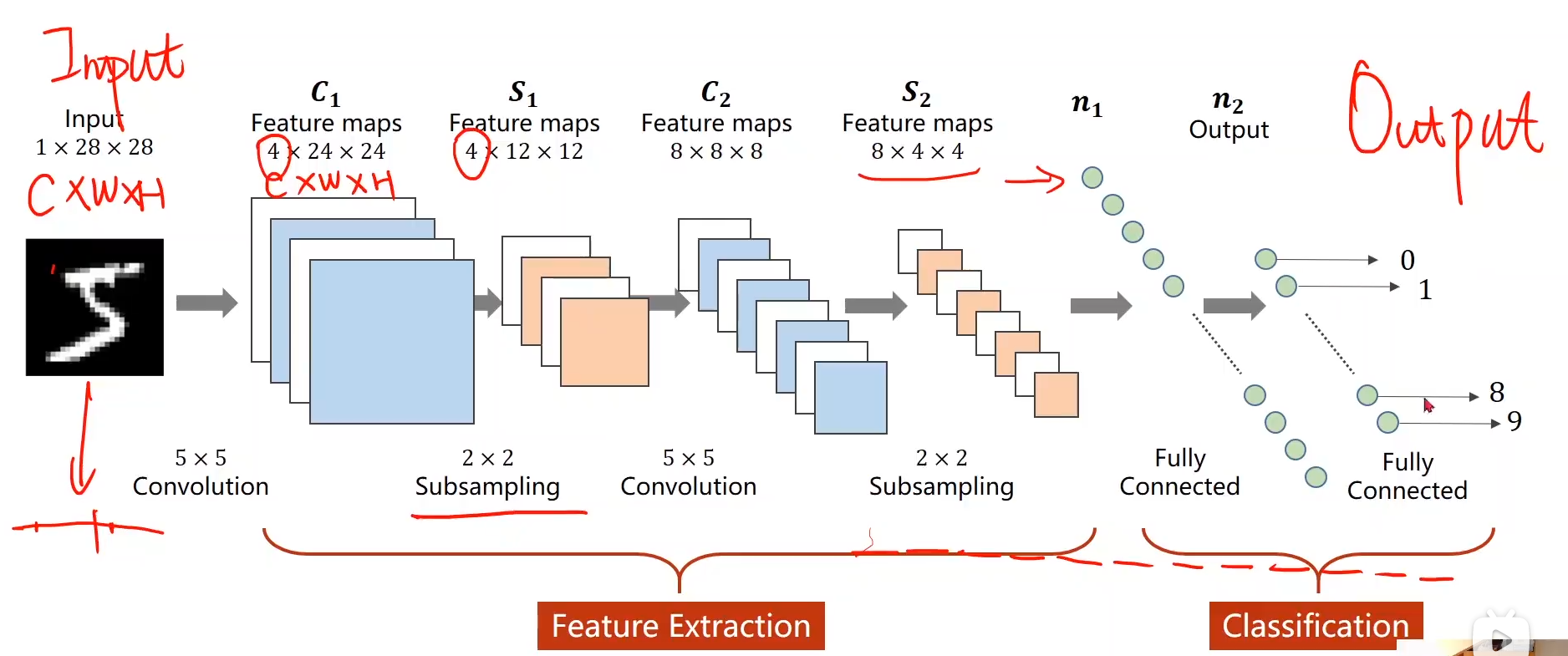
直接只进行全连接神经网络可能会导致丧失样本的一些原有的空间结构的信息

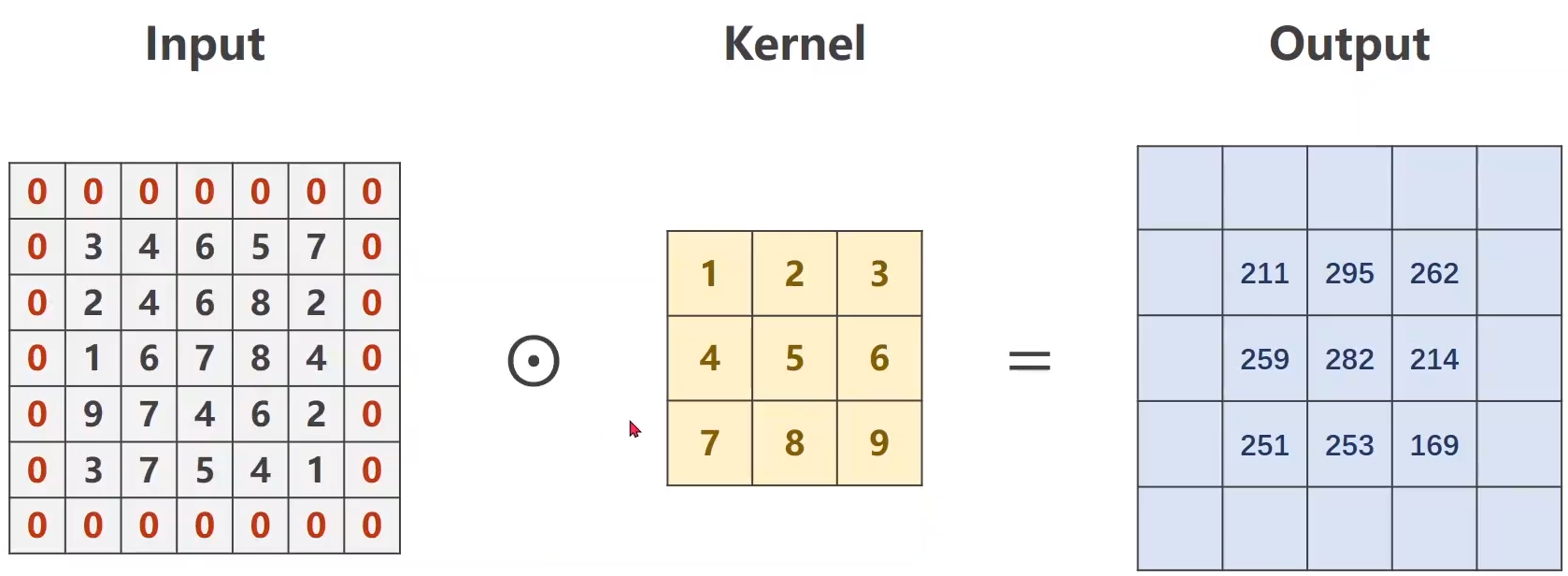
2. 卷积计算过程示例：

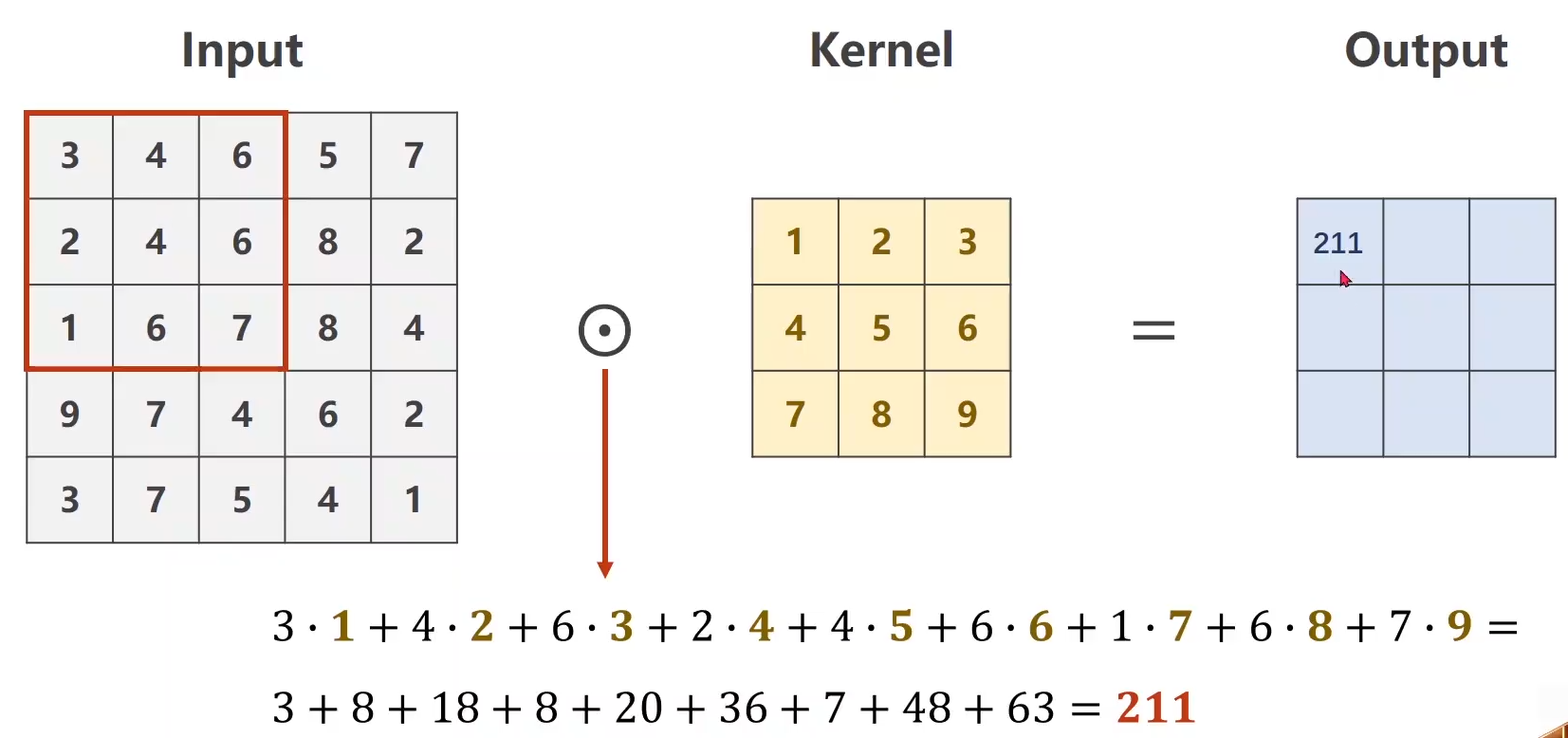
卷积运算：

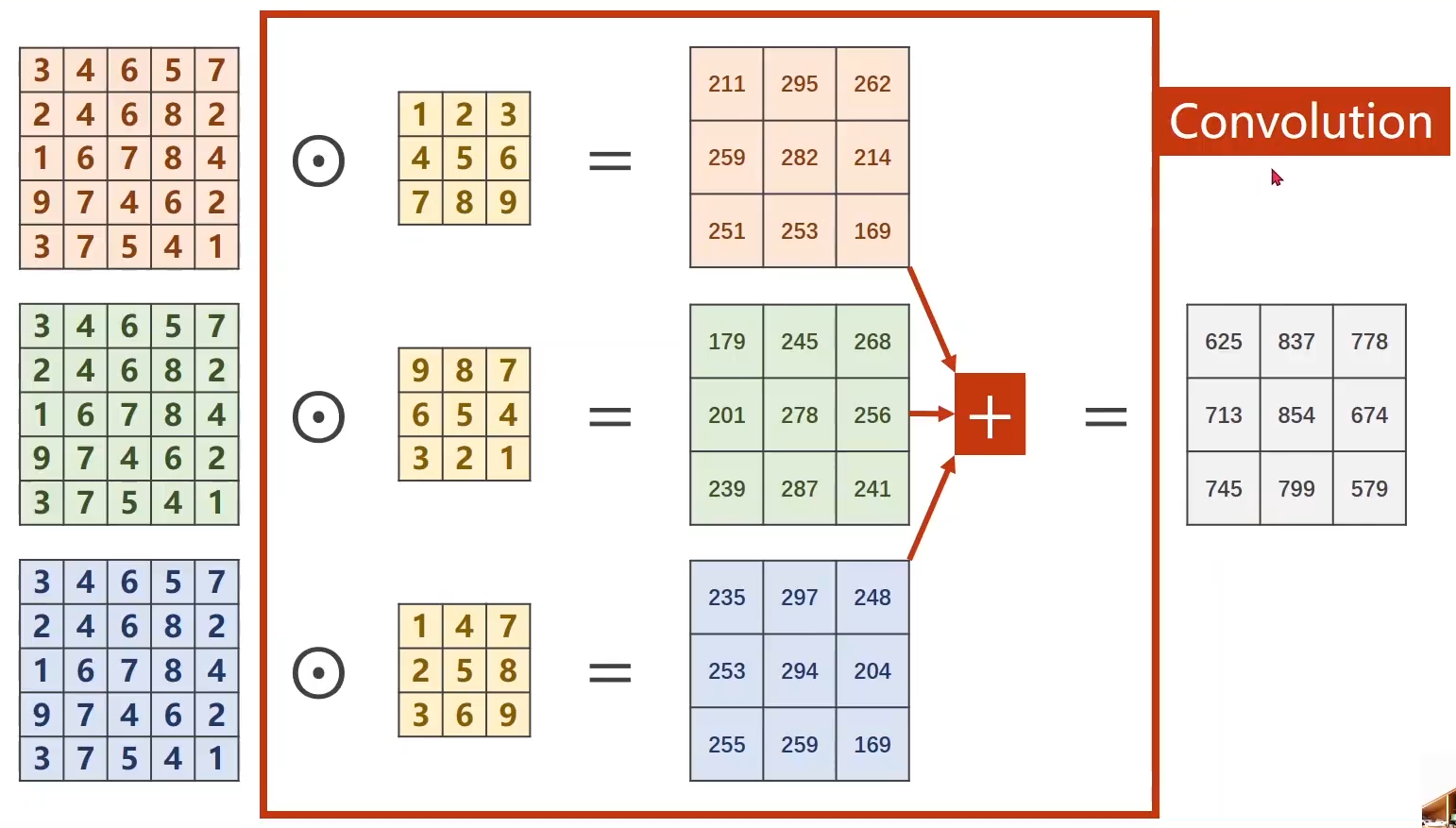
简化成下图形式:

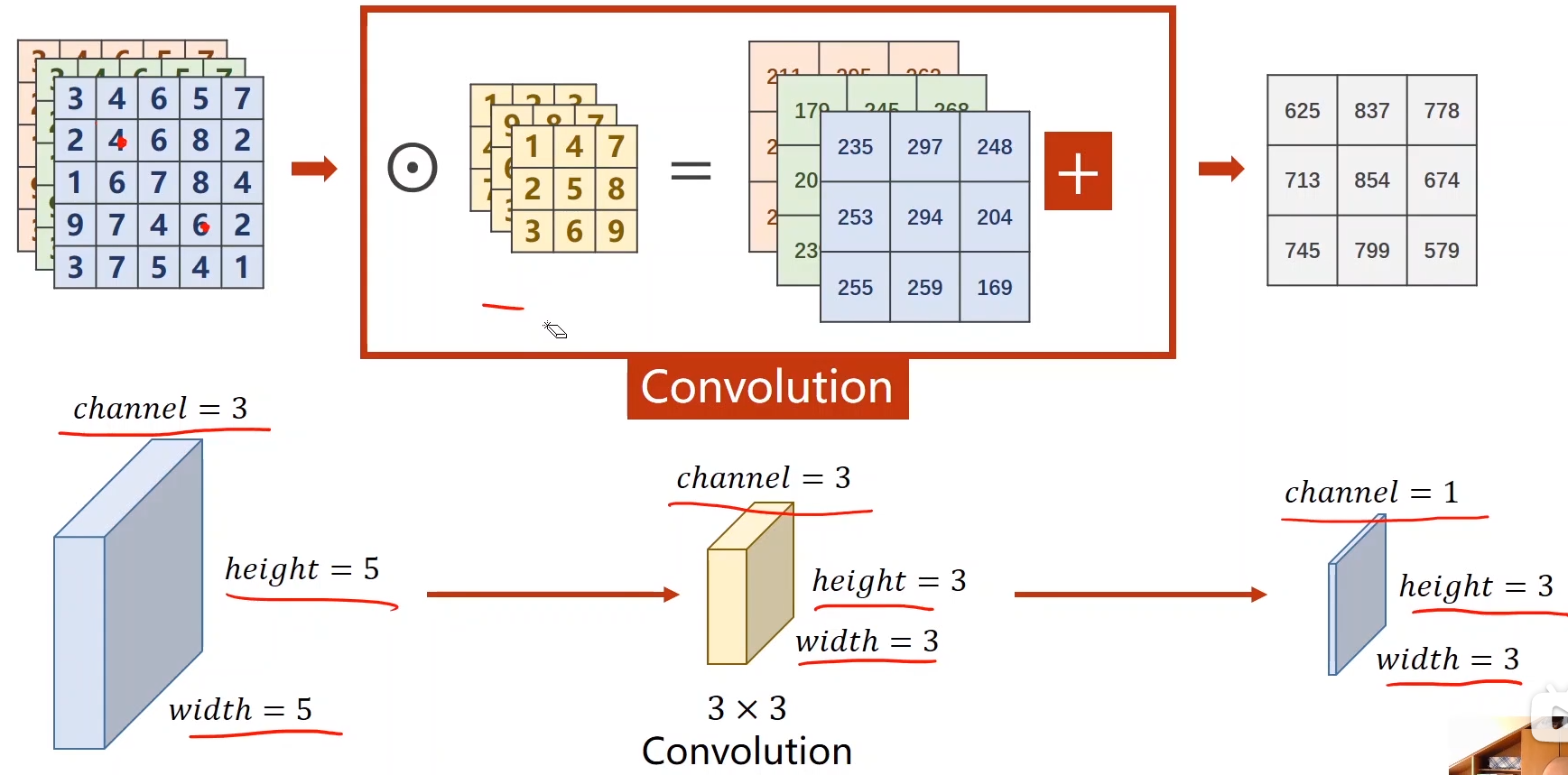
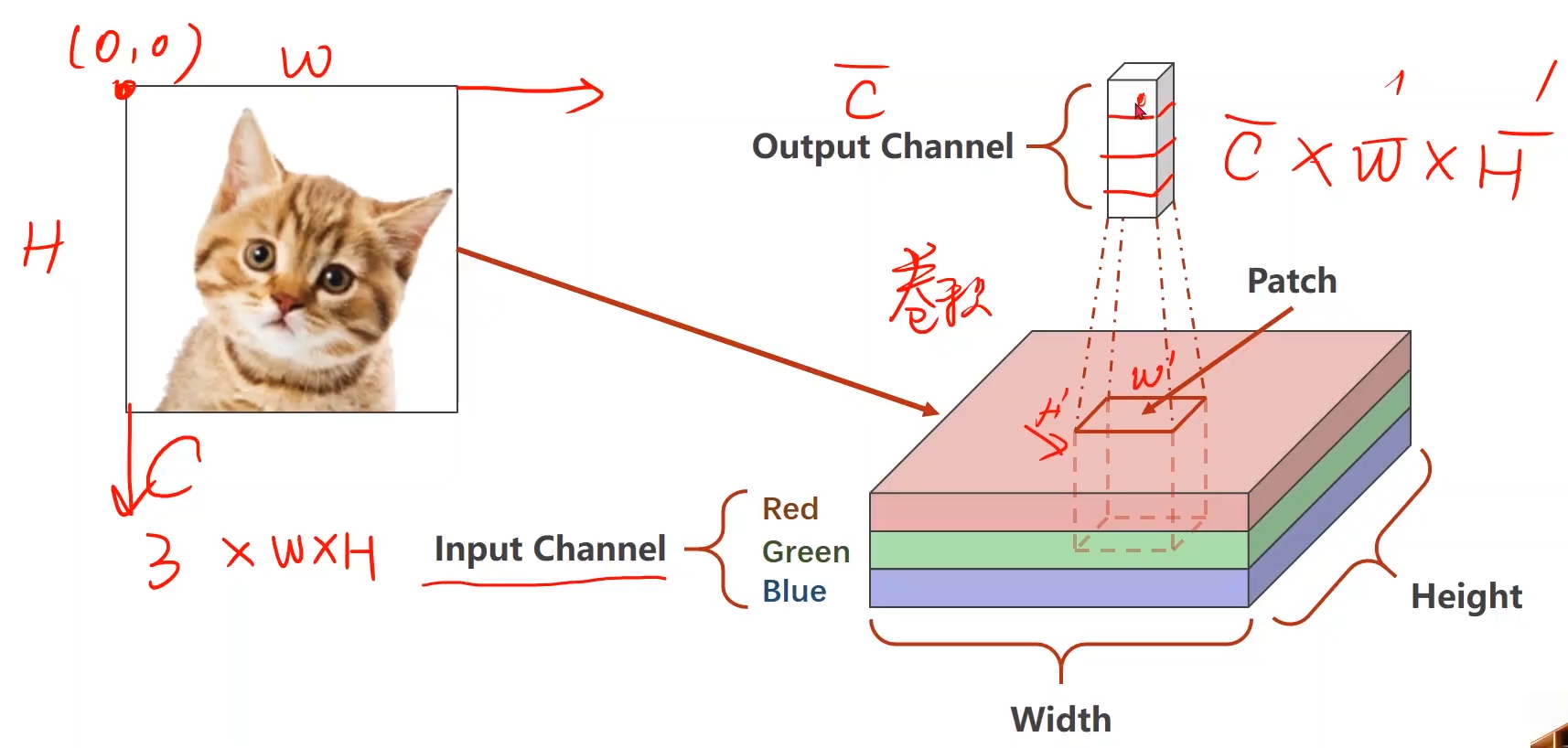
3. N通道输入 到 M通道输出：

（卷积核的channel大小(通道数)为n，卷积核的数量为m）

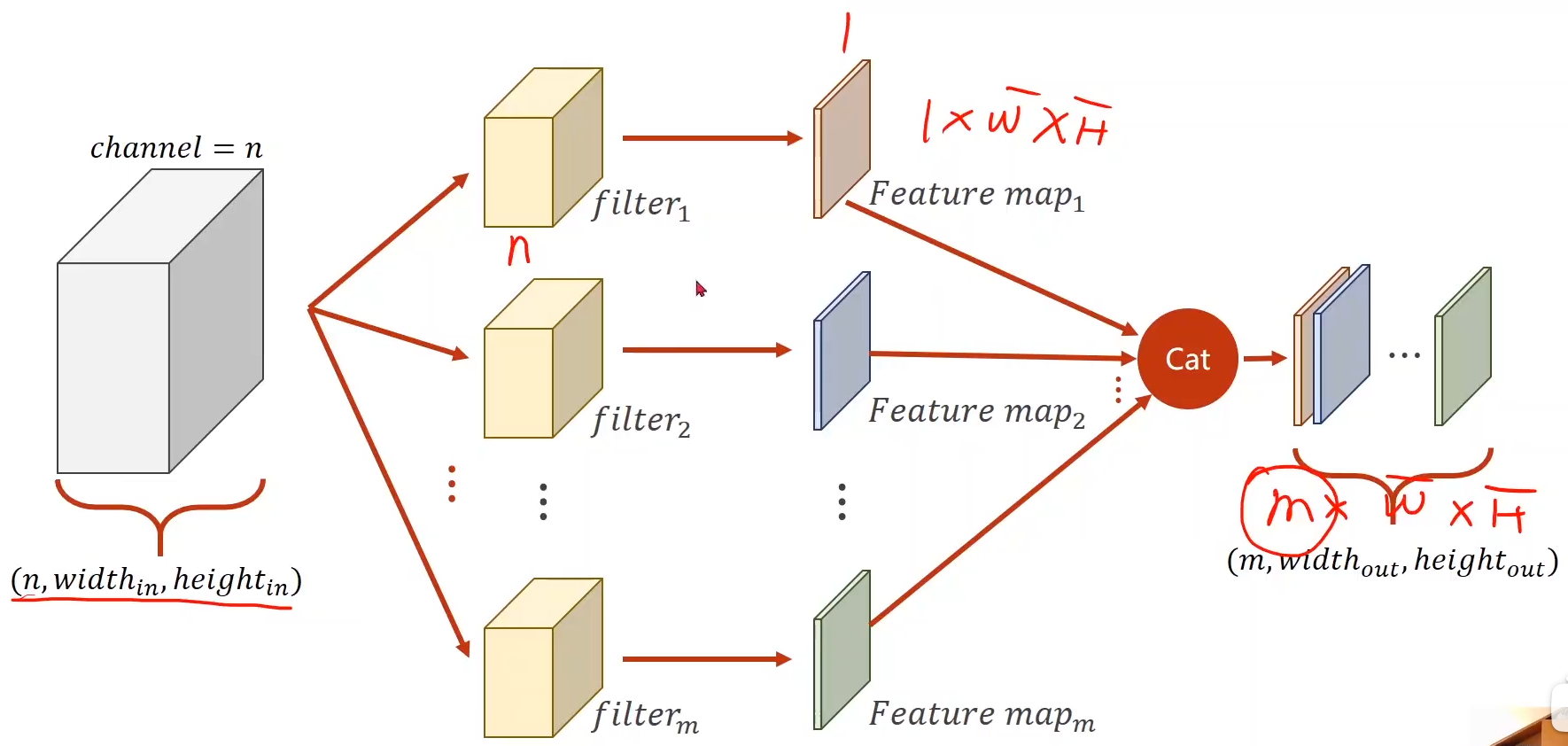
简化成下图形式：

卷积核可以拼为4维的张量

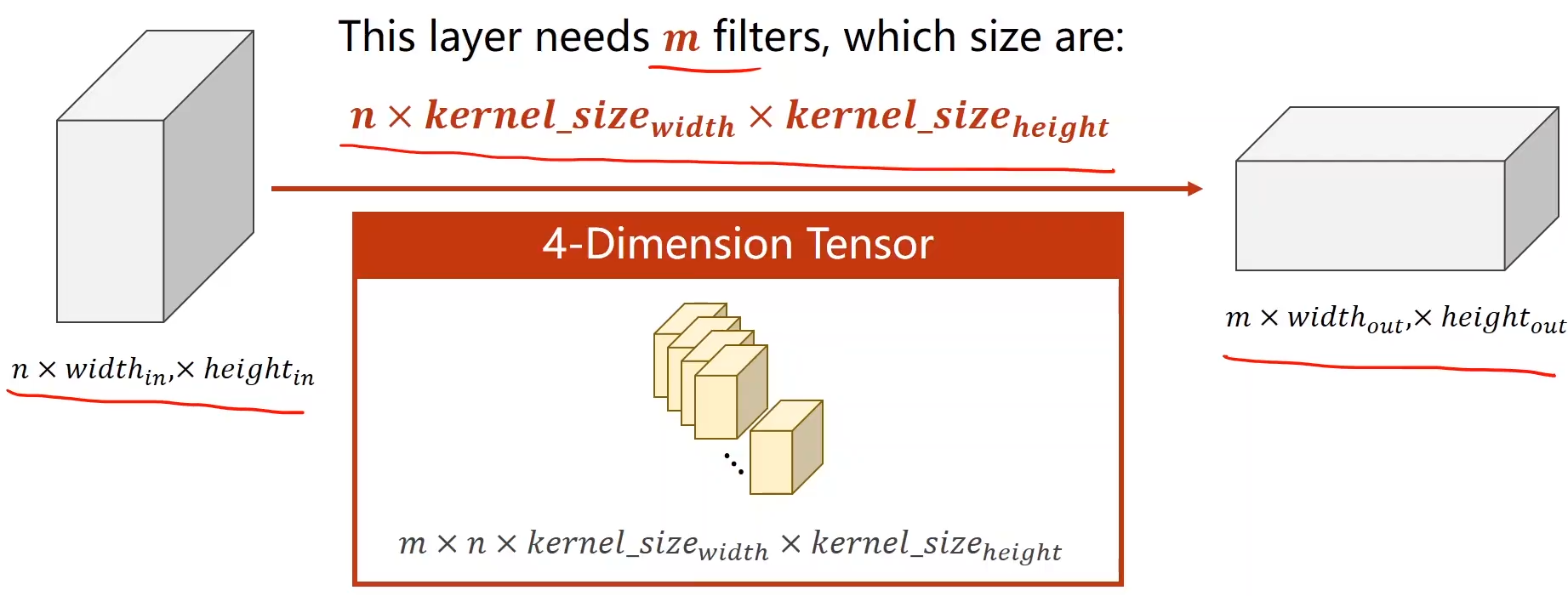
举例：5通道输入 到 10通道输出：

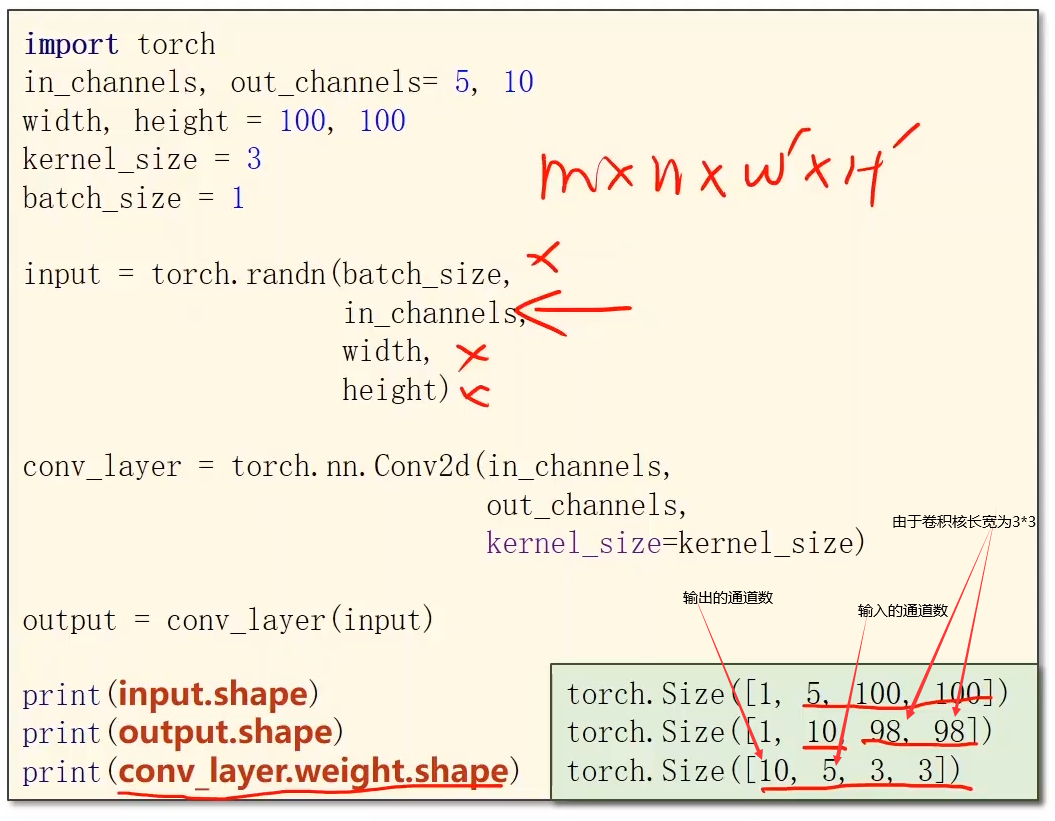
4. 关于Padding:

• padding：控制应用于输入的填充量。它可以是一个字符串 {‘valid’, ‘same’} 或一个整数元组，给出在双方应用的隐式填充量。（ controls the amount of padding applied to the input. It can be either a string {‘valid’, ‘same’} or a tuple of ints giving the amount of implicit padding applied on both sides.）

卷积核为3 * 3，外围填充1圈（3/2=1）；
卷积核为5 * 5，外围填充2圈(5/2=2)；

上述计算过程的代码:

5. 关于stride：

• stride ：控制互相关、单个数字或元组的步幅。（controls the stride for the cross-correlation, a single number or a tuple.）

可以有效降低图像的高度和宽度

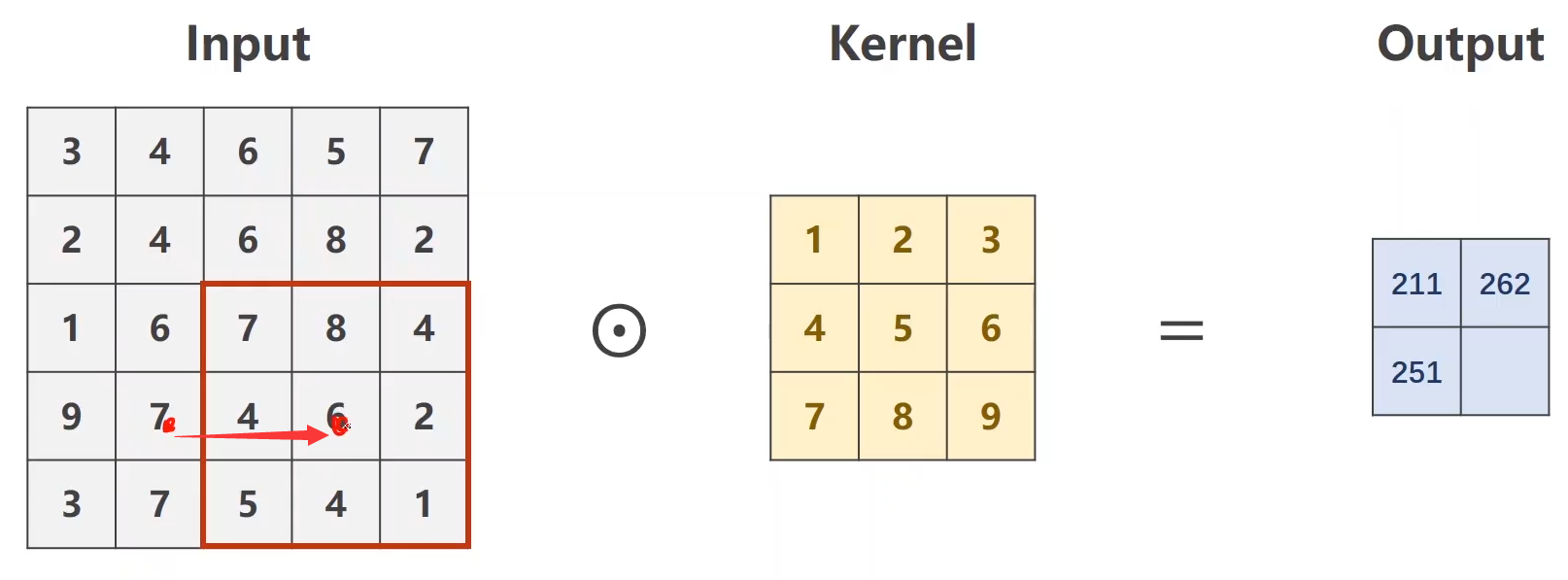
6. 关于下采样

下采样：减少数据的数据量，减低运算的需求

用的比较多的：最大池化层（选取以下四个方格中每个方格的最大值）

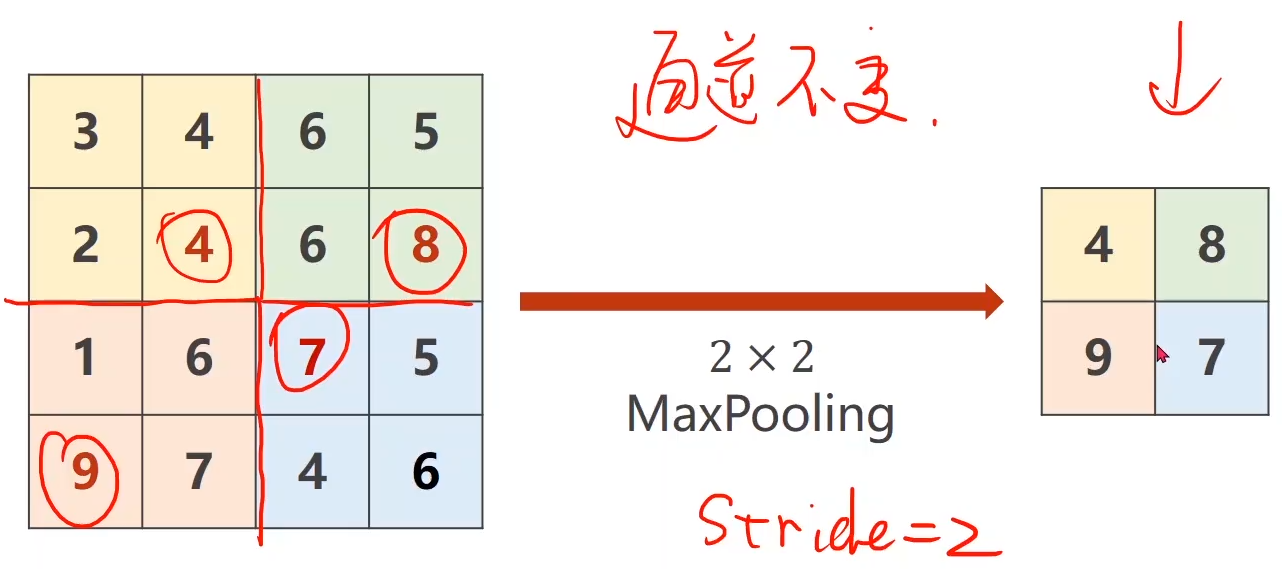
以上过程的代码：

注：当kernel_size被设成2的时候，默认的步长stride也会被设置成2；

7. 一个简单的卷积神经网络的过程：

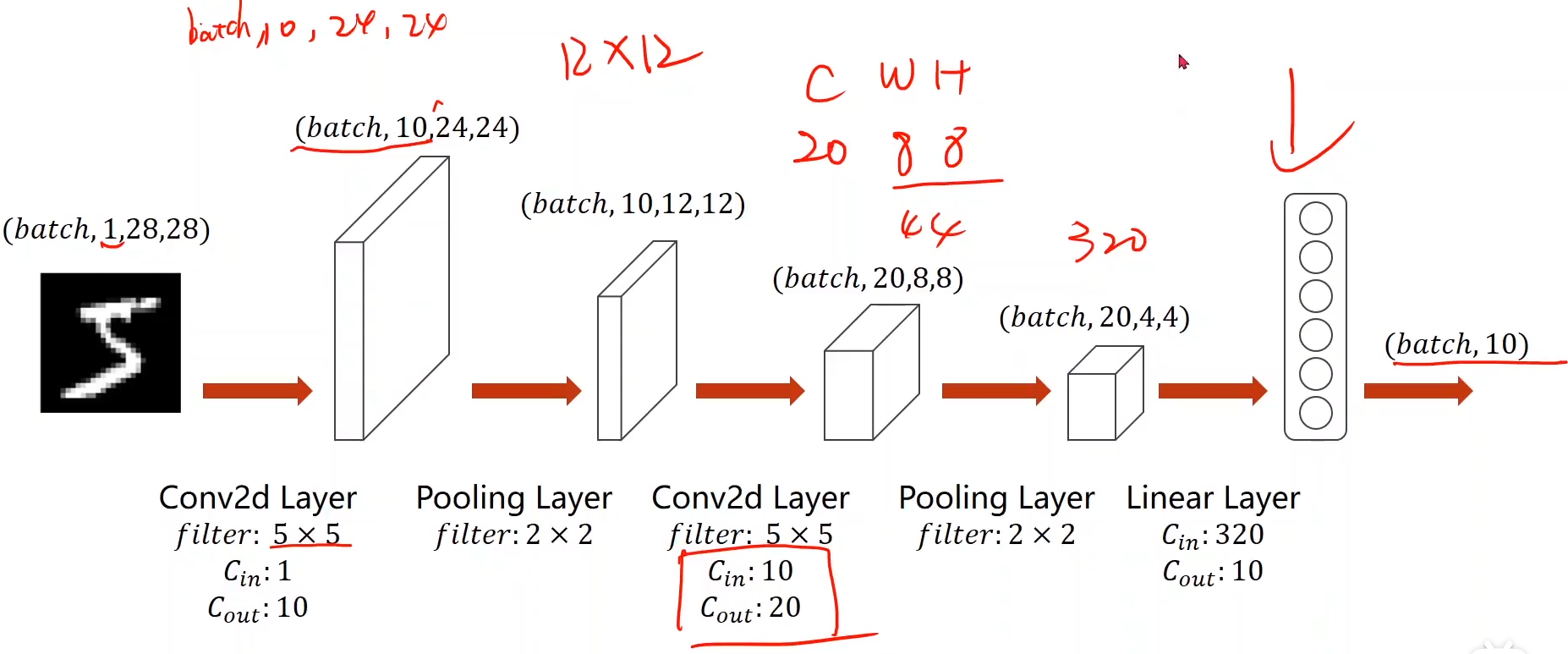
具体的流程：

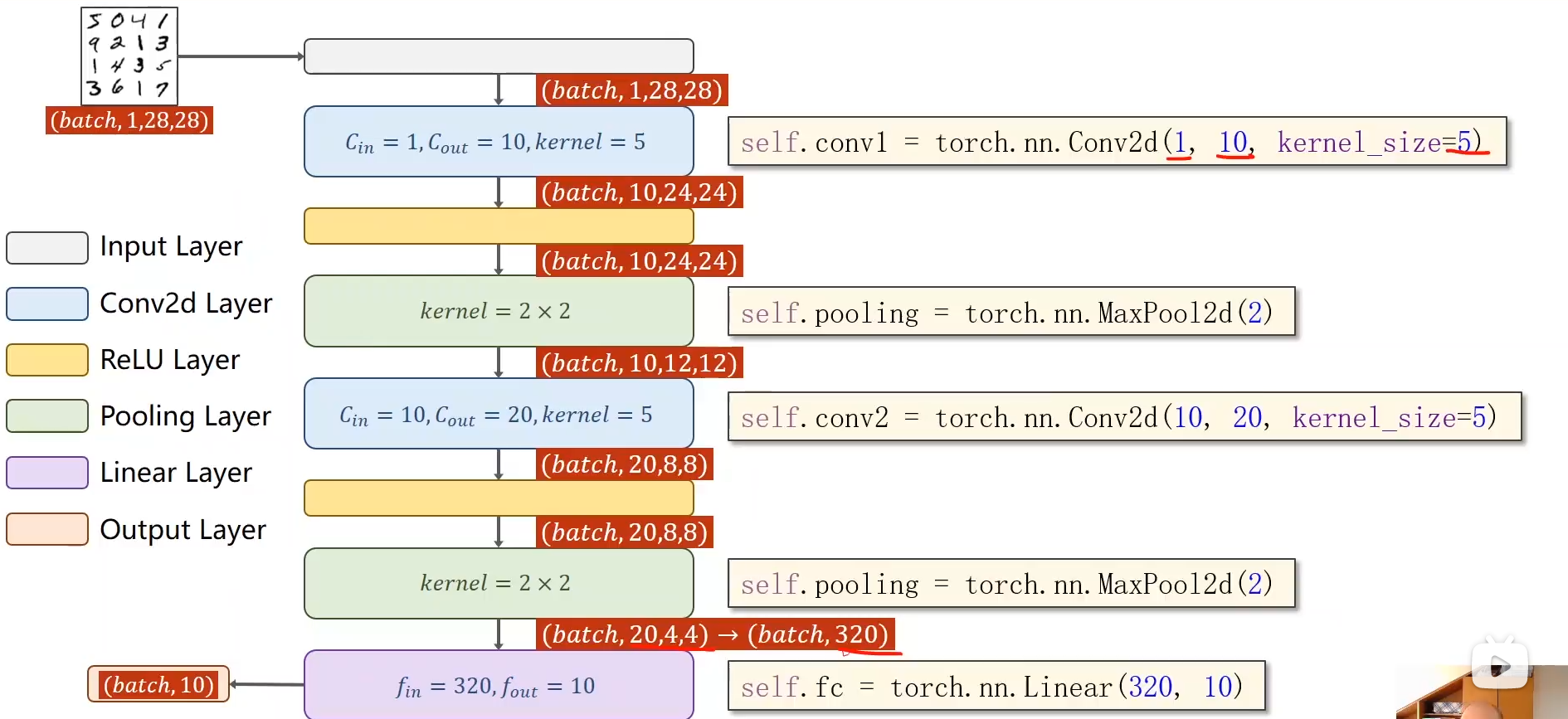
8. 怎样使用GPU来运算：

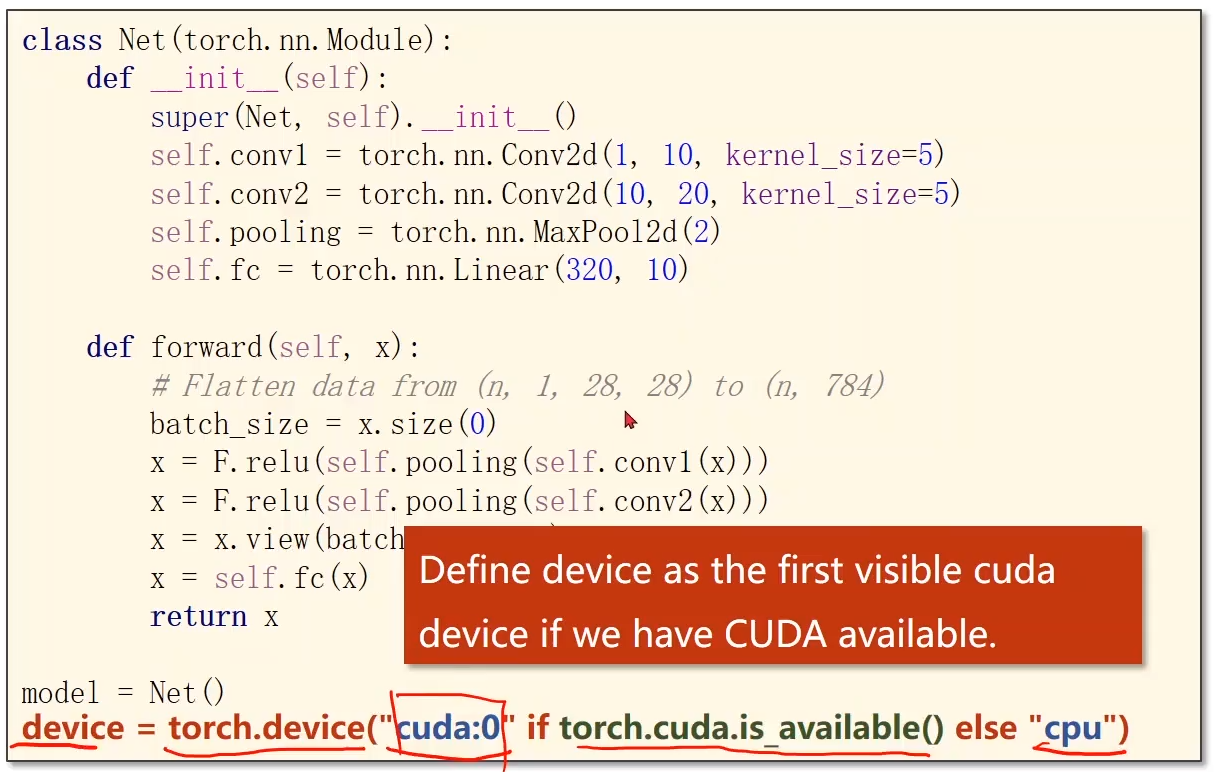
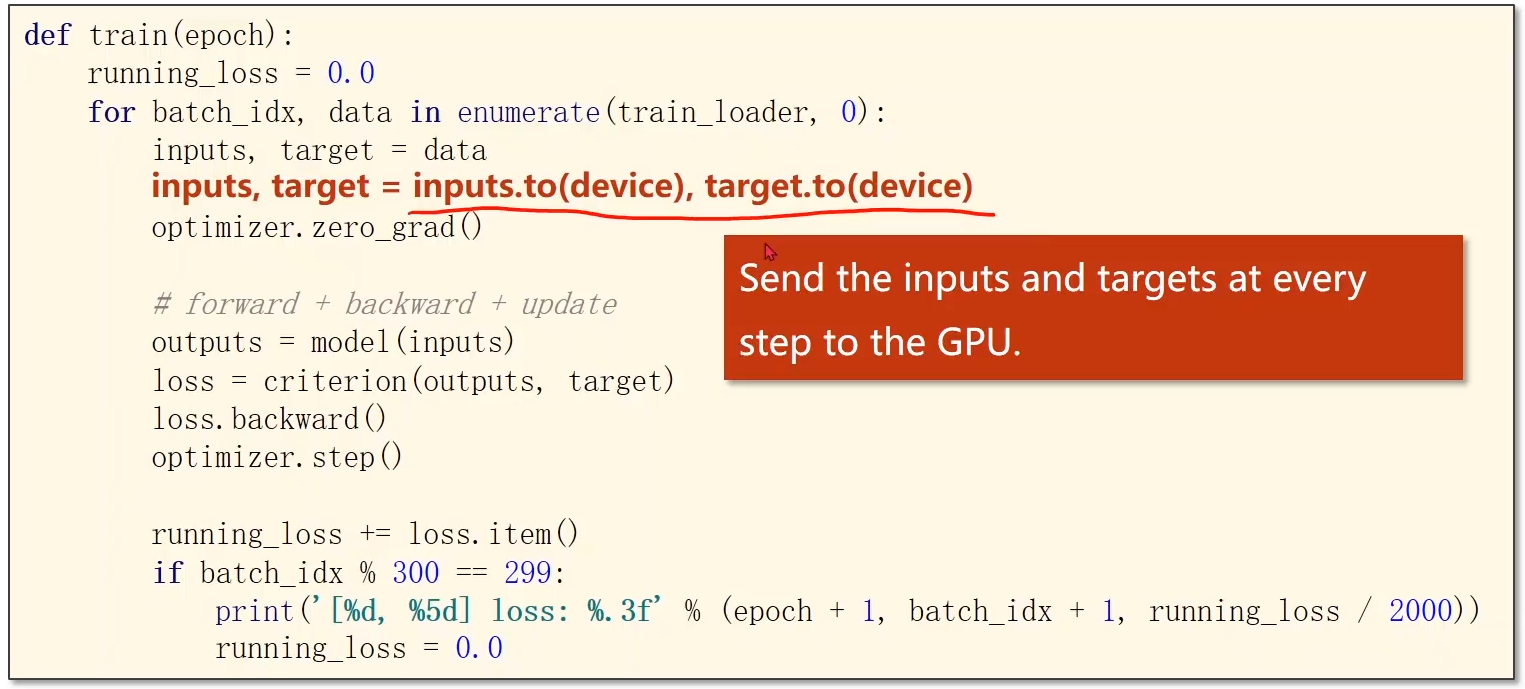
相关思考：torch.device(‘cuda‘) 与 torch.device(‘cuda:0‘) 的区别简析

程度运行时使用任务管理器查看是否正在使用GPU：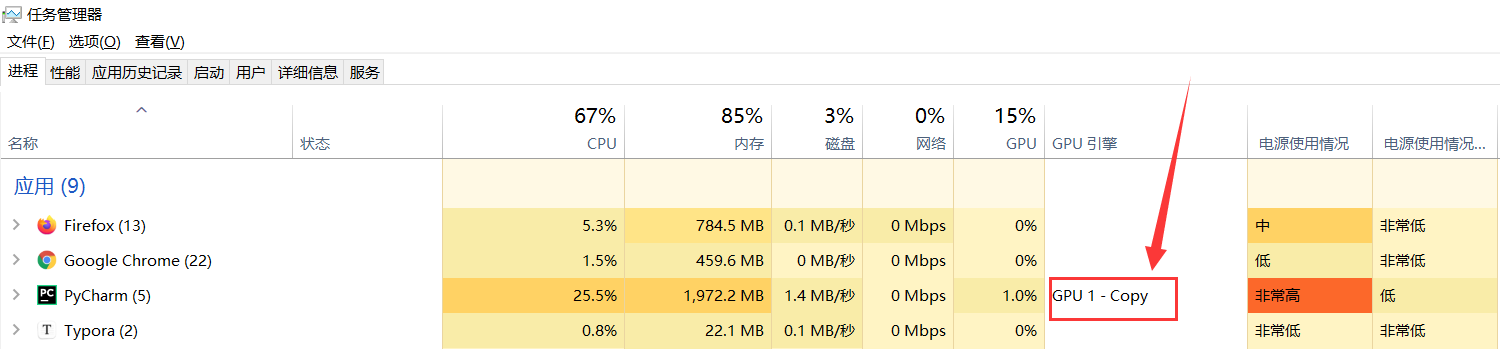

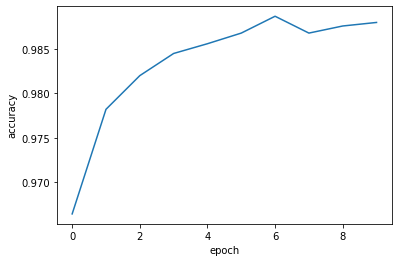
9. 程序运行结果：