平衡二叉树（AVL树）_balanced tree

为什么引入“平衡二叉树”

二叉搜索树上实现查找的时间复杂度与从根节点到所查对象节点的路径成正比，最坏情况下等于树的高度。
在构造二叉搜索树时，如果输入对象的序列恰好是按其关键码大小有序，则结果将产生一棵单支树。
例如：输入序列为{11,39,46,38,75}
在这样的树上查找所需要的时间是O(n)（与节点个数成正比）。

平衡二叉树的定义

平衡树（Balanced Tree）：高度为O(logn)的树。
平衡二叉树（Balanced Binary Tree）：由阿德尔森一维尔斯和兰迪斯（Adelson-Velskii and Landis）于1962年首先提出的，所以又称为AVL树。
空二叉树是AVL树；
如果T是一棵非空的二叉搜索树，TL和TR分别是其左子树和右子树，那么当T满足以下条件时，T是一棵AVL树：
1）TL和TR 是AVL树；
2）|hL-hR|≤1，hL和hR分别是左子树和右子树的高度

AVL树必须具备的特征

n个元素的AVL树的高度是O(logn)；
一棵n元素的AVL搜索树能在O(高度)=O(logn) 的时间内完成搜索；
将一个新元素插入到一棵n元素的AVL搜索树中，可得到一棵n+1元素的AVL树，这种插入过程可以在O(logn)时间内完成；
从一棵n元素的AVL搜索树中删除一个元素，可得到一棵n-1元素的AVL树，这种删除过程可以在O(logn)时间内完成。

AVL树的高度

假设Nh是一棵高度为h的AVL树中最小的节点数

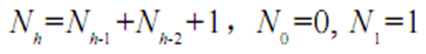
可以看到Nh的定义与斐波那契数列的定义非常相似

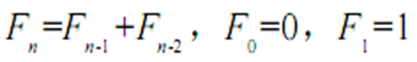
AVL树的平衡因子

为每个节点增加一个平衡因子bf。节点x 的平衡因子bf (x)定义为：bf (x)= hL-hR 。
即：x的左子树的高度-x 的右子树的高度。
从AVL树的定义可以知道，平衡因子的可能取值为-1、0、1。

如果树中任意一个结点的平衡因子的绝对值大于 1，则这棵二叉树就失去平衡。

AVL树的搜索

如果一棵AVL树有n个节点，其高度可以保持在O(logn)，因此平均搜索长度也可以保持在O(logn)。
二叉搜索树的算法完全适用于AVL树。

AVL树的插入

若一棵二叉搜索树是平衡二叉树，插入某个节点后，可能会变成非平衡二叉树；
【解决办法】对该二叉树进行平衡处理，使其变成一棵平衡二叉树。

非AVL树的平衡化处理

每插入一个新节点时，AVL树中相关节点的平衡状态会发生改变。
因此，在插入一个新节点后，需要从插入位置沿通向根的路径回溯，检查各节点的平衡因子（左、右子树的高度差）；
如果在某一节点发现高度不平衡，停止回溯；
从发生不平衡的节点起，沿刚才回溯的路径取直接下两层的节点，做平衡化旋转。

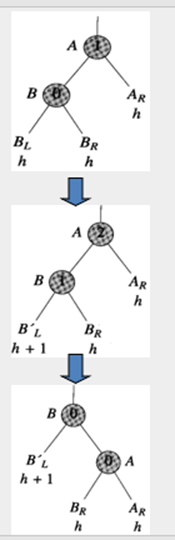
平衡化旋转

平衡化旋转有两类：
单旋转（LL旋转和LR旋转）
双旋转（LR旋转和RL旋转）
如果这三个节点处于一条直线上，则采用单旋转进行平衡化。
如果这三个节点处于一条折线上，则采用双旋转进行平衡化。

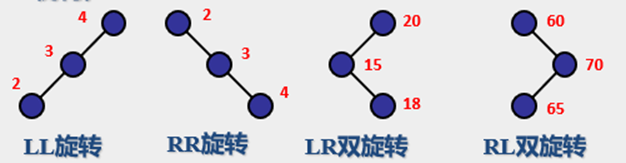
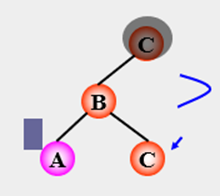
LL 平衡旋转：
若在 C 的左子树的左子树上插入
结点，使 C 的平衡因子从 1 增加
至 2， 需要进行一次顺时针旋转。 (以 B 为旋转轴）

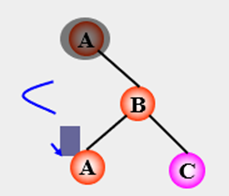
RR 平衡旋转：
若在 A 的右子树的右子树上插入
结点，使 A 的平衡因子从 -1 改变
为 -2，需要进行一次逆时针旋转。(以 B 为旋转轴）

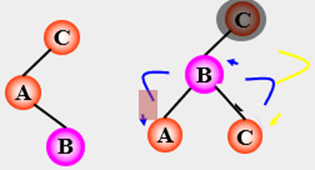
LR 平衡旋转：
若在 C 的左子树的右子树上插入
结点，使 C 的平衡因子从 1 增加
至 2， 需要先进行逆时针旋转，
再顺时针旋转。
(以插入的结点 B 为旋转轴）

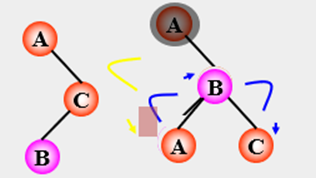
RL 平衡旋转：
若在 A 的右子树的左子树上插入
结点，使 A 的平衡因子从 -1 改变
为 -2，需要先进行顺时针旋转，再逆时针旋转。
(以插入的结点 B 为旋转轴）

调整必须保证二叉排序树的特性不变
LL旋转：新插入节点在不平衡节点的左子树的左子树中；
RR旋转：新插入节点在不平衡节点的右子树的右子树中；
LR旋转：新插入节点在不平衡节点的左子树的右子树中；
RL旋转：新插入节点在不平衡节点的右子树的左子树中。

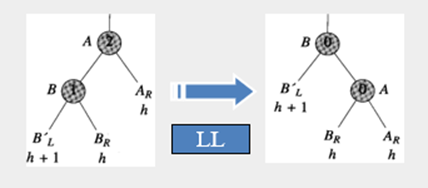
LL旋转：顺时针

在左子树D上插入新节点使其高度增1，导致节点A的平衡因子增到 2，造成了不平衡。
为使树恢复平衡，从A沿插入路径连续取3个节点A、B和D，它们处于一条方向为“/”的直线上，需要做LL旋转。
以节点B为旋转轴，将节点A顺时针旋转成为B的右孩子，B代替原来A的位置，原来B的右孩子E转为A的左孩子。
LL旋转的算法

template <class T>
void AVLTree<T>::RotateRight ( AVLNode<T> *Tree,  
                                       AVLNode<T> * &NewTree)
 {
     NewTree = Tree→left;
    Tree→left = NewTree→right;			
    NewTree→right = Tree;
}   
1
2
3
4
5
6
7
8

注：Tree为子树的根节点，NewTree为子树的新的根节点
RR旋转：逆时针

在右子树E中插入一个新节点，该子树高度增1导致节点A的平衡因子变成-2，出现不平衡。
沿插入路径检查三个节点A、C和E。它们处于一条方向为“\”的直线上，需要做RR旋转。
以节点C为旋转轴，让节点A反时针旋转成为C的左孩子，C代替原来A的位置，原来C的左孩子D转为A的右孩子。
左单旋转的算法

template <class T>
void AVLTree<T> ::RotateLeft ( AVLNode<T> *Tree,
                                       AVLNode<T> * &NewTree )
 {
     NewTree = Tree→right;
     Tree→right = NewTree→left;			         
     NewTree→left = Tree;
 }            
1
2
3
4
5
6
7
8

LR旋转：先左后右双旋转

在子树F或G中插入新节点，该子树的高度增1。节点A的平衡因子变为 2，发生了不平衡。
从节点A起沿插入路径选取3个节点A、B和E，它们位于一条形如“”的折线上，因此需要进行先左后右的双旋转。
首先以节点E为旋转轴，将节点B逆时针旋转，以E代替原来B的位置，做RR旋转。
再以节点E为旋转轴，将节点A顺时针旋转，做LL旋转，使之平衡化。
LR旋转演示

LR旋转的算法

template <class Type> void AVLTree<Type>::
LeftBalance ( AVLNode<Type> * &Tree, int & taller ) 
{   //左平衡化的算法
    AVLNode<Type> *leftsub = Tree→left,  *rightsub;
    switch ( leftsub→balance )
    {
       case -1 :  //LL旋转，此处是hR-hL=-1
          Tree→balance = leftsub→balance = 0;
          RotateRight ( Tree, Tree );
          taller = 0;  break;	
       case 0 :
          cout << “树已经平衡化.\n";  break;       
case 1 :
               rightsub = leftsub→right;
	    switch ( rightsub→balance ) 
              {	
                case -1: Tree→balance = 1;
                              leftsub→balance = 0;  
                              break;
                case 0 : Tree→balance = leftsub→balance = 0;
    	  	         break;		
	     case 1 : Tree→balance = 0;
   		            leftsub→balance = -1;
                              break;
               }
             rightsub→balance = 0;	
             RotateLeft ( leftsub, Tree→left );  先RR旋转
             RotateRight ( Tree, Tree );             后LL旋转
             taller = 0;		                 
       }
   }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

RL旋转：先右后左双旋转

右左双旋转是左右双旋转的镜像。
在子树F或G中插入新节点，该子树高度增1。节点A的平衡因子变为-2，发生了不平衡。
从节点A起沿插入路径选取3个节点A、C和D，它们位于一条形如“”的折线上，需要进行先右后左的双旋转。
首先做LL旋转：以节点D为旋转轴，将节点C顺时针旋转，以D代替原来C的位置。
再做RR旋转：以节点D为旋转轴，将节点A反时针旋转，恢复树的平衡。
RL旋转的算法

template <class Type> void AVLTree<Type>::
RightBalance ( AVLNode<Type> * &Tree, int & taller ) 
{   //右平衡化的算法
    AVLNode<Type> *rightsub = Tree→right, *leftsub;
    switch ( rightsub→balance ) 
   {				             
       case 1 :  //RR旋转，此处是hR-hL=1
           Tree→balance = rightsub→balance = 0;
           RotateLeft ( Tree, Tree );  
           taller = 0;  break;
      case 0 : cout << “树已经平衡化.\n";  break;
      case -1 : leftsub = rightsub→left;
switch ( leftsub→balance )
           {		
	     case 1 : Tree→balance = -1;   
                            rightsub→balance = 0;  break;
	     case 0 : Tree→balance = 
                                 rightsub→balance = 0;  break;
               case -1 : Tree→balance = 0;  
                            rightsub→balance = 1;  break;
	 }
	 leftsub→balance = 0;
	 RotateRight ( rightsub, Tree→left );  LL旋转
            RotateLeft ( Tree, Tree );  taller = 0;  RR旋转
     }
}		
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

建立一棵AVL树

从一棵空树开始，通过输入一系列对象的关键值，逐步建立AVL树，在插入新节点时使用前面所给的算法进行平衡旋转。
例：输入关键值序列为 { 16, 3, 7, 11, 9, 26, 18, 14, 15 }，构造一棵AVL树
{ 16, 3, 7, 11, 9, 26, 18, 14, 15 }，插入和调整过程如下：

AVL树的删除

设q是被删除节点的父节点，
如果删除发生在q的左子树，那么bf (q) 减1，
如果删除发生在q的右子树，那么bf (q) 加1；
根据q的平衡因子，存在三种现象：

现象1

如果q新的平衡因子bf(q)=0，意味着删除前bf(q)=1或者bf(q)=-1，只有单子树
此时高度减1，需改变父节点和其他某些祖先节点的平衡因子

现象2

如果q新的平衡因子bf(q)=1或-1，意味着删除前bf(q)=0，左右子树高度一样
此时高度不变，需改变父节点和其他某些祖先节点的平衡因子

现象3

如果q新的平衡因子bf(q)=-2或2，意味着删除前bf(q)=-1或1，左右子树高度不同
此时树在q节点是不平衡的，需要平衡化处理

平衡因子为2或-2的两种情况

设A是第一个删除后bf(A)=2的节点，则删除前bf(A)=1，B为A的左子树的根节点；
根据节点B的平衡因子，bf(B)=0、1、-1；
L型不平衡：删除发生在A的左子树，又可细分为L0、L1、L-1三种；
R型不平衡：删除发生在A的右子树，又可细分为R0、R1、R-1三种；
R0表示删除发生在A的右子树且bf(B)=0。
R1表示删除发生在A的右子树且bf(B)=1。
R-1表示删除发生在A的右子树且bf(B)=-1。

R0类型的平衡化处理

删除发生在A的右子树 且 bf(B) = 0
与LL型旋转类似，区别在于仅在于A和B最后的平衡因子。

R1类型的平衡化处理

删除发生在A的右子树 且 bf(B) = 1
与LL型旋转相同

R-1类型的平衡化处理

删除发生在A的右子树 且 bf(B) = -1
与LR型旋转相同

欢迎大家加我微信交流讨论（请备注csdn上添加）