一、分类:
1、参考:http://www.cnblogs.com/heaad/archive/2011/03/07/1976443.html
例子:
%读取训练数据
[f1,f2,f3,f4,class] = textread('trainData.txt' , '%f%f%f%f%f',150);
%特征值归一化
[input,minI,maxI] = premnmx( [f1 , f2 , f3 , f4 ]') ;
%构造输出矩阵
s = length( class) ;
output = zeros( s , 3 ) ;
for i = 1 : s
output( i , class( i ) ) = 1 ;
end
%创建神经网络
net = newff( minmax(input) , [10 3] , { 'logsig' 'purelin' } , 'traingdx' ) ;
%设置训练参数
net.trainparam.show = 50 ;
net.trainparam.epochs = 500 ;
net.trainparam.goal = 0.01 ;
net.trainParam.lr = 0.01 ;
%开始训练
net = train( net, input , output' ) ; %这里的input矩阵的行表示特征的维度,列代表一个样本;output'每一列表示一个样本的标签。
%读取测试数据
[t1 t2 t3 t4 c] = textread('testData.txt' , '%f%f%f%f%f',150);
%测试数据归一化
testInput = tramnmx ( [t1,t2,t3,t4]' , minI, maxI ) ;
%仿真
Y = sim( net , testInput )
%统计识别正确率
[s1 , s2] = size( Y ) ;
hitNum = 0 ;
for i = 1 : s2
[m , Index] = max( Y( : , i ) ) ;
if( Index == c(i) )
hitNum = hitNum + 1 ;
end
end
sprintf('识别率是 %3.3f%%',100 * hitNum / s2 )
步骤:
1、数据预处理——归一化
在训练神经网络前一般需要对数据进行预处理,一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法。
(1) 什么是归一化?
数据归一化,就是将数据映射到[0,1]或[-1,1]区间或更小的区间,比如(0.1,0.9) 。
(2) 为什么要归一化处理?
<1>输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
<2>数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。
<3>由于神经网络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数,由于S形函数的值域限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
<4>S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(X)在参数a=1时,f(100)与f(5)只相差0.0067。
(3) 归一化算法
一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式:
<1>
y = ( x - min )/( max - min )
其中min为x的最小值,max为x的最大值,输入向量为x,归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间,当激活函数采用S形函数时(值域为(0,1))时这条式子适用。
<2>
y = 2 * ( x - min ) / ( max - min ) - 1
这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数(值域为(-1,1))时这条式子适用。
(4) Matlab数据归一化处理函数
Matlab中归一化处理数据可以采用premnmx , postmnmx , tramnmx 这3个函数。
<1> premnmx
语法:[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
参数:
pn: p矩阵按行归一化后的矩阵
minp,maxp:p矩阵每一行的最小值,最大值
tn:t矩阵按行归一化后的矩阵
mint,maxt:t矩阵每一行的最小值,最大值
作用:将矩阵p,t归一化到[-1,1] ,主要用于归一化处理训练数据集。
<2> tramnmx
语法:[pn] = tramnmx(p,minp,maxp)
参数:
minp,maxp:premnmx函数计算的矩阵的最小,最大值
pn:归一化后的矩阵
作用:主要用于归一化处理待分类的输入数据。
<3> postmnmx
语法: [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)
参数:
minp,maxp:premnmx函数计算的p矩阵每行的最小值,最大值
mint,maxt:premnmx函数计算的t矩阵每行的最小值,最大值
作用:将矩阵pn,tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。
2、
2. 使用Matlab实现神经网络
使用Matlab建立前馈神经网络主要会使用到下面3个函数:
newff :前馈网络创建函数
train:训练一个神经网络
sim :使用网络进行仿真
下面简要介绍这3个函数的用法。
(1) newff函数
<1>newff函数语法
newff函数参数列表有很多的可选参数,具体可以参考Matlab的帮助文档,这里介绍newff函数的一种简单的形式。
语法:net = newff ( A, B, {C} ,‘trainFun’)
参数:
A:一个n×2的矩阵,第i行元素为输入信号xi的最小值和最大值;
B:一个k维行向量,其元素为网络中各层节点数;
C:一个k维字符串行向量,每一分量为对应层神经元的激活函数;
trainFun :为学习规则采用的训练算法。
<2>常用的激活函数
a) 线性函数 (Linear transfer function)

该函数的字符串为’purelin’。
b) 对数S形转移函数( Logarithmic sigmoid transfer function )

该函数的字符串为’logsig’。
c) 双曲正切S形函数 (Hyperbolic tangent sigmoid transfer function )

也就是上面所提到的双极S形函数。
该函数的字符串为’ tansig’。
Matlab的安装目录下的toolbox\nnet\nnet\nntransfer子目录中有所有激活函数的定义说明。

<3>常见的训练函数
常见的训练函数有:
traingd :梯度下降BP训练函数(Gradient descent backpropagation)
traingdx :梯度下降自适应学习率训练函数
<4>网络配置参数
一些重要的网络配置参数如下:
net.trainparam.goal :神经网络训练的目标误差
net.trainparam.show : 显示中间结果的周期
net.trainparam.epochs :最大迭代次数
net.trainParam.lr : 学习率
(2) train函数
网络训练学习函数。
语法:[ net, tr, Y1, E ] = train( net, X, Y )
参数:
X:网络实际输入
Y:网络应有输出
tr:训练跟踪信息
Y1:网络实际输出
E:误差矩阵
(3) sim函数
语法:Y=sim(net,X)
参数:
net:网络
X:输入给网络的K×N矩阵,其中K为网络输入个数,N为数据样本数
Y:输出矩阵Q×N,其中Q为网络输出个数
二、拟合
例子:拟合曲线 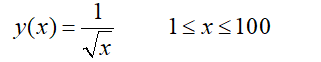
程序:
function BPalg()
clear;
%X=-4*pi:0.05:4*pi;
X=1:100;
Y=[];
Y_test=[];
P=length(X);
for i=1:P
Y(i)=1/X(i)^0.5
%Y(i)=(sin(X(i))/X(i))^2;
%Y(i)=exp(-X(i)^2)*sin(X(i)^2);
end
scatter(X,Y,10,'b');
grid on;
hold on;
net=newff(minmax(X),[14,1],{'logsig' 'purelin'},'traingdx'); %一个隐藏层,含有神经元14个
net.trainparam.epochs = 1000;
net.trainparam.goal = 0.0001 ;
net.trainParam.lr = 0.001 ;
net = train(net,X,Y);
for i=1:P
Y_test(i) = sim(net,X(i));
end
plot(X,Y_test,'r');
hold off;
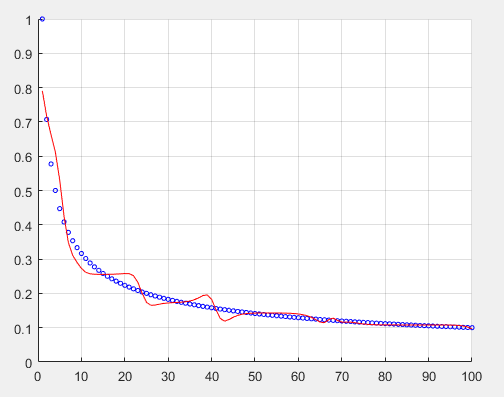
这里不需对数据归一化;


