2020第十一届蓝桥杯C/C++ 省赛A组 题解_第十一届蓝桥杯a 分配口罩

A

624
遍历每个数，取余判断每一位

#include<iostream>
using namespace std;

int main()
{
	int cnt=0;
	for(int i=1;i<=2020;i++)
	{
		int tmp=i;
		while(tmp)
		{
			if(tmp%10==2)
				cnt++;
			tmp/=10;
		}
	}
	cout<<cnt;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

B

2481215
两个循环，判断最大公约数是否为1

#include<iostream>
using namespace std;

int gcd(int a,int b)
{
	if(b==0)
	return a;
	else 
	return gcd(b,a%b);	
}

int main()
{
	int cnt=0;
	for(int i=1;i<=2020;i++)
		for(int j=1;j<=2020;j++)
			if(gcd(i,j)==1)
				cnt++;
	cout<<cnt;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

C

761
直接找规律比较快
（1,1） 1=0+1
（2,2） 5=（1+2）+2
（3,3） 13=（1+2+3+4）+3
（i，i） x=（1+2+3+…+2(i-1)）+i=(i-1)(2i-1)+i
附蛇形填数代码

#include<iostream>
using namespace std;

int a[1001][1001];

int main()
{
	int cnt=1;
	int i=1,j=1;
	a[i][j]=cnt;
	while(cnt<10000)
	{
		
		if(i==1)
			j++;
		a[i][j]=++cnt;
		while(j>1)
			a[++i][--j]=++cnt;
		if(j==1)
			i++;
		a[i][j]=++cnt;
		while(i>1)
			a[--i][++j]=++cnt;
	}
	cout<<a[20][20];
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

D

80
建图，dfs。每个灯可以亮或者不亮，枚举2^7.。

#include<iostream>
using namespace std;

const int N=8;
int map[N][N],fa[N],vis[N],ans;

int getfa(int i)										//寻找根节点 
{
	if(fa[i]==i)
		return i;
	return fa[i]=getfa(fa[i]);							//压缩路径 
}

void dfs(int k)
{
	if(k>7)												//7个灯都枚举完了 
	{
		for(int i=1;i<=7;i++)							//先把自己设为自己的父节点 
			fa[i]=i;
		for(int i=1;i<=7;i++)
			for(int j=1;j<=7;j++)
			{
				if(map[i][j]&&vis[i]&&vis[j])			//将连通且亮着的灯，并在一块 
				{
					int faa=getfa(i),fab=getfa(j);
					if(faa!=fab)
						fa[faa]=fab;
				}
			}
		int cnt=0;
		for(int i=1;i<=7;i++)							//有几个根节点说明有几个集合 
			if(fa[i]==i&&vis[i])						//亮着的灯的集合数 
				cnt++;
		if(cnt==1)										//都连通的话，只有一个集合 
			ans++;							
		return;
	}
	vis[k]=1;											//k灯亮  dfs中k+1亮和灭 
	dfs(k+1);
	vis[k]=0;											//k灯灭 
	dfs(k+1);
}

int main()
{
	map[1][2]=map[2][1]=1;map[1][6]=map[6][1]=1;	//连通的存图 
	map[6][7]=map[7][6]=1;map[6][5]=map[5][6]=1;
	map[2][7]=map[7][2]=1;map[2][3]=map[3][2]=1;
	map[5][7]=map[7][5]=1;map[5][4]=map[4][5]=1;
	map[3][7]=map[7][3]=1;map[4][3]=map[3][4]=1;
	dfs(1);
	cout<<ans;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

E

1391
任意线（包括直线与曲线）之间，不交于同一点，则能将平面分为尽可能多的部分
根据欧拉定理 V−E+F−T=1,T=0 ，求解出 F=1+E−V ，只需求解出点数 V 与边数 V 即可求解
根据我们的分析，任意两直线即可有一交点，个数为 (202) ；任意两圆之间有两个交点，个数为 2⋅(202) ；任意圆与直线之间有两个交点，个数为 20×20×2
故 V=(202)+2⋅(202)+20×20×2=1370
同样根据我们的分析，一条直线被剩余的 19 条直线各交于一点，被 20 个圆各交于两点，故线上有 19+20×2=59 个点，一条直线被分为 60 条边；一个圆被剩余的 19 个圆、 20 条直线各交于两点，共 (19+20)×2=78 个点，一个圆被分为 78 条边
故 E=60×20+78×20=2760
因此得到答案： F=1+2760−1370=1391

F

#include<iostream>
#include<cstdio>
using namespace std;

int a[100001];

int main()
{
	int n,maxx=-1,minn=101;
	cin>>n;
	long long s=0;
	double ave;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		s+=a[i];
		maxx=max(maxx,a[i]);
		minn=min(minn,a[i]);
	}
	ave=s/double(n);
	printf("%d\n%d\n%.2lf",maxx,minn,ave);	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

G

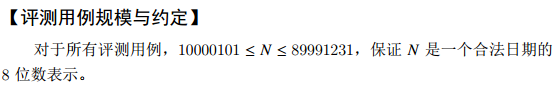
判断每一个日期，将日期取余，得到每一位存入数组，判断对应为是否相等
注意判断日期合法

#include<iostream>
using namespace std;

int main()
{
	int n,ans1=0,ans2=0;
	int a[10];
	cin>>n;
	for(int i=n+1;;i++)
	{
		int j=1;
		int tmp=i;
		while(j<=8)
		{
			a[j++]=tmp%10;
			tmp/=10;
		}
		bool flag=0;
		int m=a[5]*10+a[6],k=a[7]*10+a[8],y;
		switch(m)
		{
			case 4:
			case 6:
			case 9:
			case 11:
				if(m>30) flag=1;
				break;
			case 2:
				y=a[1]*1000+a[2]*100+a[3]*10+a[4];
				if((y%4==0&&y%100!=0)||y%400==0) {if(m>29) flag=1;break;}
				else {if(m>28) flag=1;break;}
			default:
				if(m>31) flag=1;
				break;	
		}
		if(flag)
			continue;
		if(a[1]==a[3]&&a[1]==a[6]&&a[1]==a[8]&&a[2]==a[4]&&a[2]==a[5]&&a[2]==a[7])
			for(int j=8;j;j--)
			{
				ans2*=10;
				ans2+=a[j];
			}
		if(a[1]==a[8]&&a[2]==a[7]&&a[3]==a[6]&&a[4]==a[5]&&!ans1)
			for(int j=8;j;j--)
			{
				ans1*=10;
				ans1+=a[j];
			}
		if(ans1&&ans2)
			break;	
	}
	cout<<ans1<<endl<<ans2;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

H

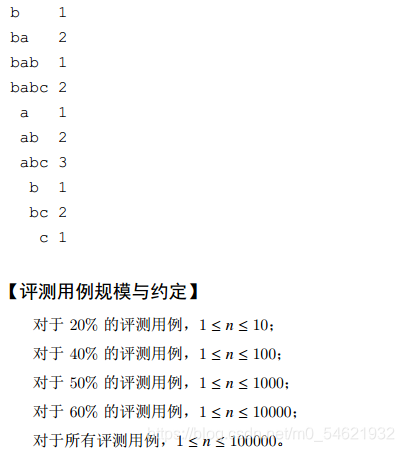
可以枚举，三重循环，这么算，n需小于100，显然不行
每一个字母贡献的子串数，为其下标分别与前一个相同字母下标和后一个相同字母下标相减的绝对值相乘，再累计每一个字母即为答案

比如图中这个字符串，记算4号位a的贡献子串数
前一个a下标为1，后1个为6 （4-1）*（6-4）=6
解释一下 4-1 对应着bca（234号） 6-4对应着ab（45号）
分别以bca为起始位置，ba为终止位置的子串都只包含4号a，且是全部只包含4号a的子串
即为bca bcab ca cab a ab
注意初始，可能前面或者后面没有相同字母

#include<iostream>
#include<string>
using namespace std;

const int N=1e5+5;
int pre[N],nex[N],a[27];
string s;

int main()
{
	cin>>s;
	s="0"+s;						//下标从1开始 
	int n=s.length()-1;				//长度 
	for(int i=1;i<=n;i++)			//寻找前一个相同字符下标 
	{
		int c=s[i]-'a';
		pre[i]=a[c];
		a[c]=i;
	}
	for(int i=0;i<26;i++)			//初始化，可能后边没有相同字符    寻找前一个时，未初始，因为a数组默然为0 
		a[i]=n+1;
	for(int i=n;i;i--)				//寻找后一个相同字符下标 
	{
		int c=s[i]-'a';
		nex[i]=a[c];
		a[c]=i;
	}
	long long int ans=0;
	for(int i=1;i<=n;i++)
		ans+=(long long)(i-pre[i])*(nex[i]-i);//相乘计算累加
	cout<<ans; 
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

I

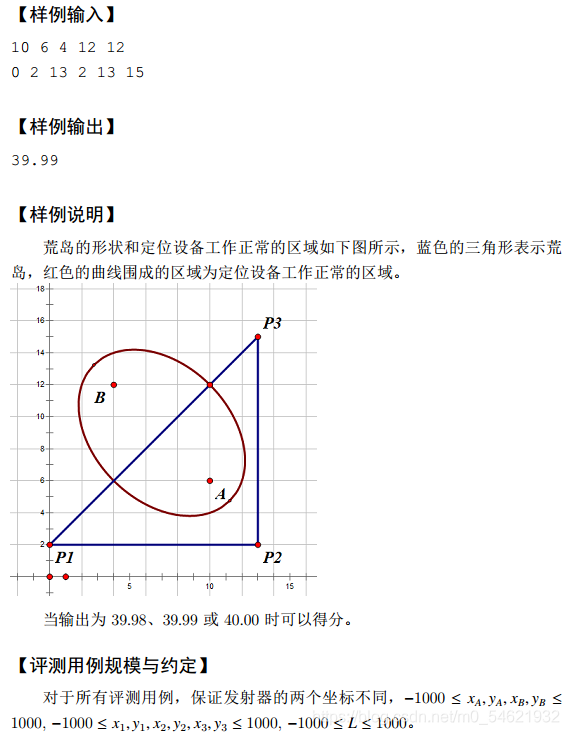
求椭圆和三角形重叠部分的面积，恕我不会

J

呃呃呃，还是不会
谁会，教教我 orz