我家自动化

这个屌丝很懒，什么也没留下！

热门标签

Resnet残差网络|卷积神经网络|原理|新人总结_残差神经网络

作者：我家自动化 | 2024-03-25 13:05:41

踩

残差神经网络

前言：本文是作者初学cnn与resnet总结。本文尽量多的涉及相关知识，但许多并未详细介绍；读者可以提取关键词自行搜索，或查看参考连接。如果你是新手，强烈推荐参考中的视频课程和文章。此外，文章若有错误之处，希望评论留言。

1 卷积神经网络基础

1.1 传统神经网络与卷积神经网络

常规神经网络，的输入是一个向量，然后在一系列的隐层中对它做变换。每个隐藏层都是由若干的神经元组成，每个神经元都与前一层中的所有神经元连接。

如果输入为一个尺寸为256x256x3的一张RGB色彩模式图像，会让神经网络至少包含200x200x3=120000个权重值和相应的偏差值。并且对一般来说，网络中还有着多个隐藏层和神经元。显而易见这会产生大量的参数。所以这种全连接方式效率低下，大量的参数也很快会导致网络过拟合。

传统神经网络

卷积神经网络的结构正基于输入数据是图像的假设。我们就向结构中添加了一些特有的性质。这些特有性质使得前向传播函数实现起来更高效，并且大幅度降低了网络中参数的数量。

卷积神经网络

1.2 卷积神经网络结构

1.2.1 输入层

对于图像分类任务，输入层是H ∗ W ∗ C的图像，其中H是指图像的长度，W是图像的宽度，C指的是图像的channel数，一般灰度图的channel数为1，彩色图的channel数为3。

1.2.2 卷积层

卷积层卷积神经网络的核心。其将图像分成很多小区域，对于整个原始输入图像按照一个区域进行加权得到特征图，每个特征图的每个元素是相应位置卷积的结果。我们可以利用内积（对应位置相乘）然后加上偏置来计算。

如图是一个channel数为3的图像的单一卷积核的计算过程（其中+1为偏置）：

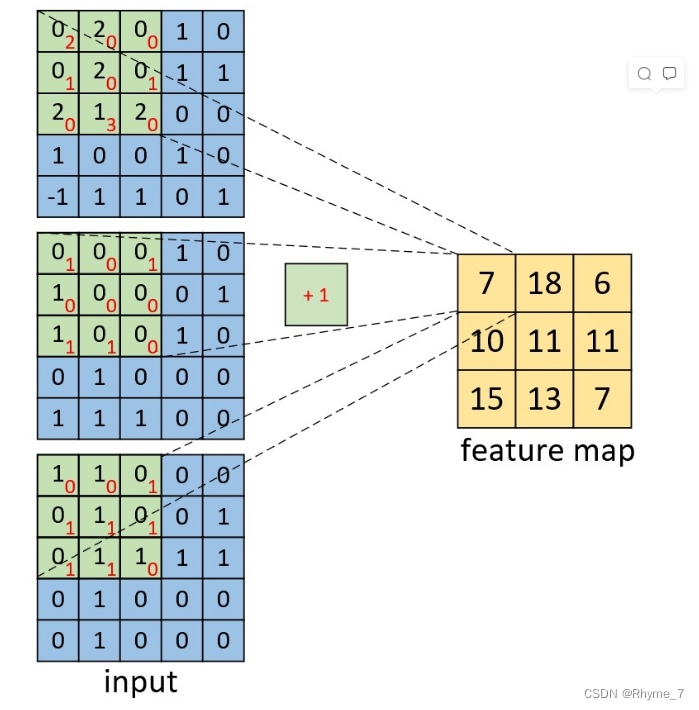
在卷积层中有这些参数参数：

滑动窗口步长S（步长越小能移动越多，得到的特征图越大，提取的特征越细腻）。

卷积核尺寸K（选择区域的大小等于最后得到结果个数的大小）。

边缘填充P（由于步长选择，有些元素重复加权贡献的，越往里的点贡献多，越往外的点贡献少，是边界点贡献多些，在外面加上一圈0，可以弥补一些边界特征缺失）zero padding 以0为值进行边缘填充。

卷积核个数：等于得特征图的个数。

1.2.3 池化层

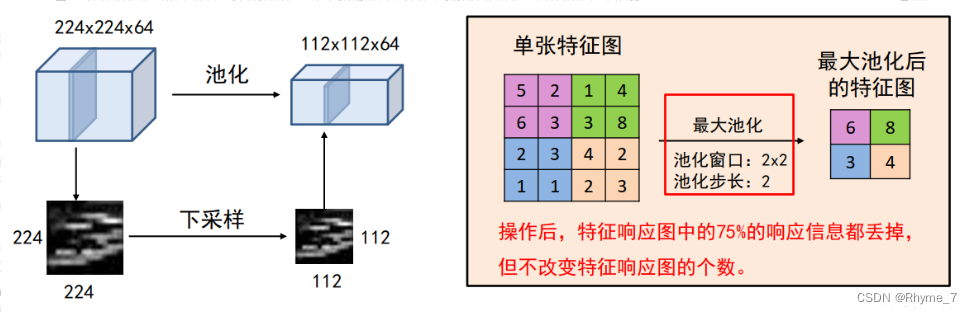
池化操作将输入矩阵某一位置相邻区域的总体统计特征作为该位置的输出。换句话说，就是对特征图的压缩。如此减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合。

主要有平均池化（Average Pooling）、最大池化（Max Pooling）等。池化层参数有池化窗口和池化步长。

1.2.4 批量归一化层

在预处理时，我们会对图像进行标准化，这样能加速收敛。但是经过卷积计算之后特征图变成了新的数据分布，这时再进行计算可能会导致梯度的消失。为此引入Batch Normalization使特征图满足均值为0，方差为1的分布规律。

1.2.5 激活函数与全连接层

激活函数为模型引入非线性因素，卷积神经网络中常用到Relu即f(u)=max(0,u)。全连接层在卷积神经网络中起到分类器的作用。即上述层将输入特征提取，通过全连接层得出分类。

2 Resnet解决了网络的深度问题

在计算机视觉领域，神经网络的深度很重要。深的网络能够提取到更多维度的特征。但是Resnet之前的深层网络难训练而且效果不好难以突破，甚至达到一定程度后越深反而效果越差。

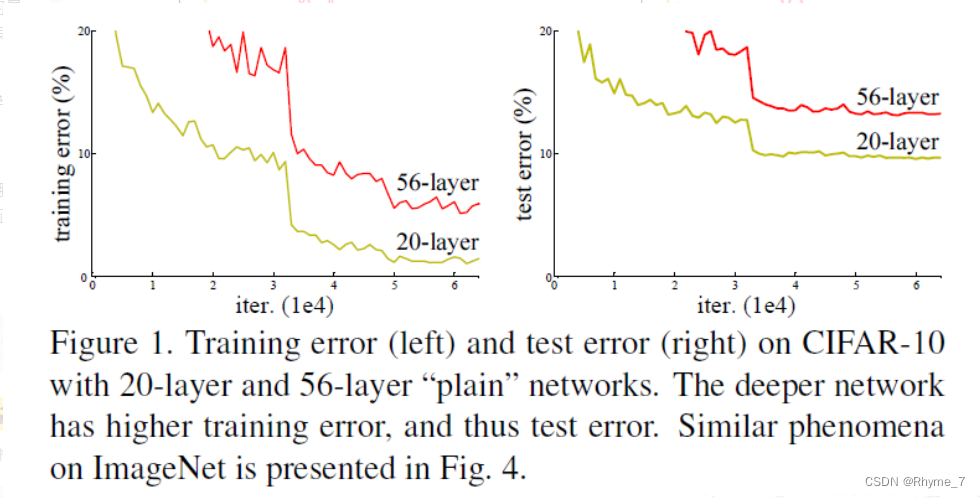
下图是resnet作者用传统网络得到的结果统计。与20层网络相比，56层网络在训练和测试中误差都更大；且在较少层数的网络中批量归一化和梯度下降法已经能够很大程度上解决梯度消失和收敛速度的相关问题。所以这显然不是梯度消失引起的过拟合现象。

我们称这种现象为网络退化现象。即随着网络深度的增加，准确率开始达到饱和并且在之后会迅速下降。针对这个问题，何恺明等人提出了残差网络ResNet，并且拿到了2015年ImageNet图像识别挑战赛的冠军。甚至在CIFAR-10上达到了1000层。

2.1 嵌套函数与非嵌套函数

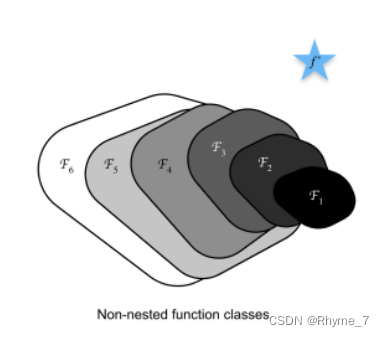
图中蓝色五角星表示最优值。Fi闭合区域表示函数。在该区域中可以找到一个最优模型（区域中的一个点），并用它到最优值的距离来衡量模型的优劣。上图为非嵌套函数，可以看出随复杂度的不断增加，虽然函数的区域面积增大了，但是在该区域中所能找到的最优模型（区域内的一点）离最优值的距离可能会越来越远。我们可以理解为模型走偏了。而下图为嵌套函数，每一次增加函数复杂度之后函数所覆盖的区域会包含原来函数所在的区域。也就是说，增加函数的复杂度只会使函数所覆盖的区域在原有的基础上进行扩充，而不会偏离原本存在的区域。

对于深度神经网络，如果能将新添加的层训练成恒等映射（identify function）f(x) = x，新模型和原模型将同样有效；同时，由于新模型可能得出更优的解来拟合训练数据集，因此添加层不会导致效果变差。

3 Resnet核心思想与结构

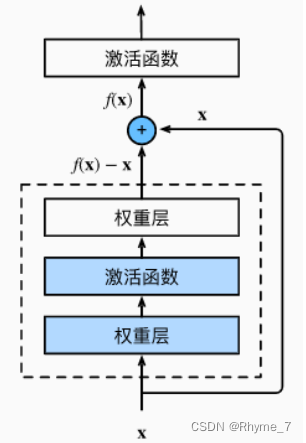
假设学习的目标是f（x），x是浅层的输出。虚线框是新加入的层。按照传统的我们直接去学习f（x）即可。但是Resnet中新加入的层学习的是f（x）-x。输出时将两者相加得到f（x）。因此对新的网络来说，它的训练错误率至少不会比浅层网络更差。

换一种说法，f（x）为理想映射、f（x）-x为残差映射。实际情况下残差映射更容易优化。并且当理想映射 f(x) 极接近于恒等映射时，残差映射易于捕捉恒等映射的细微波动。

除此之外，如果以恒等映射 f(x) = x 作为所想要学出的理想映射 f(x)，只需要将残差块中虚线框内加权运算的权重和偏置参数设置为 0。在残差块中，输入可以通过跨层数据线路更快地传播。

3.1 残差块细节

残差块首先有2个相同输出通道数的3 * 3卷积层，每个卷积层后面接一个批量归一化层和ReLu激活函数；通过跨层数据通路，跳过残差块中的两个卷积运算，将输入直接加在最后的ReLu激活函数前。

这种设计要求2个卷积层的输出与输入形状一样，这样才能使第二个卷积层的输出和原始的输入形状相同，才能进行相加。

如果想要改变通道数，就需要引入一个额外的1 * 1的卷积层来将输入变换成需要的形状后再做相加运算，即上述右图。原理是1*1卷积层在空间维度上不做任何的东西，主要是在通道维度上做改变，选择一个1*1卷积使得输出通道是输入通道的两倍，这样就能将残差连接的输入和输出对应起来。在ResnNet里面，如果把输出通道数翻了两倍，那么输入的高和宽会减小一半，所以这里步幅设置为2，使在高宽和通道上都能匹配上。此外还有两种方式：填零和投影，Resnet作者进行了实验对比选择了上述方案。

3.2 各种层数的残差结构

通过配置不同的通道数和模块中的残差块数可以得到不同的ResNet模型。

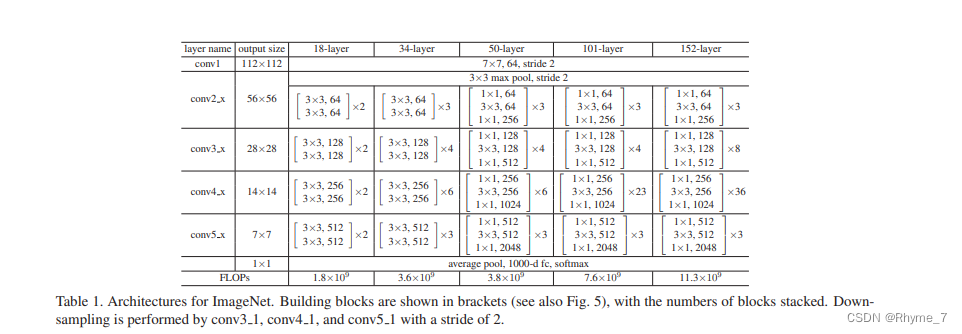
上表中表中残差块×N 表示将该残差结构重复N次。

下图为18层resnet详细结构，其中k、s、p为卷积层的三个参数。实线为3.1左图结构，虚线为3.1右图结构。

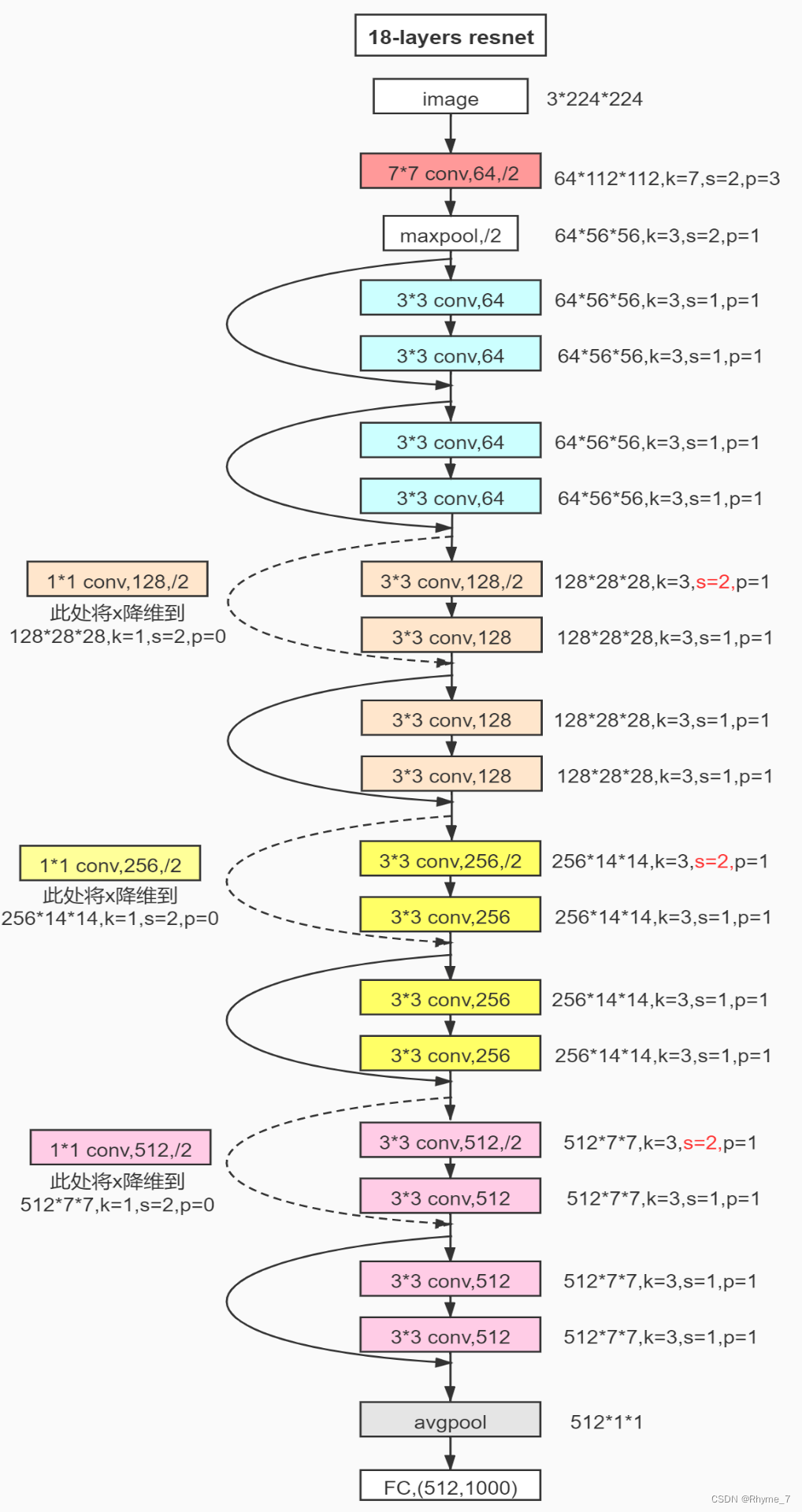
3.2.1 更深的bottleneck design

在本小节的第一幅图中，可以看到当层数达到50以上，出现了一种结构稍有变化的残差块。如下图所示

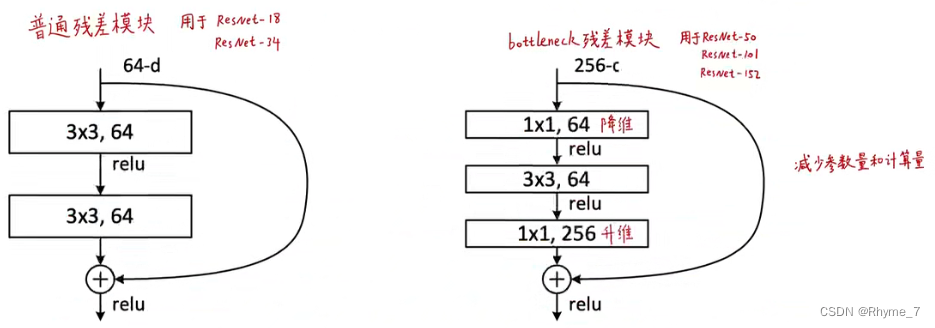
首先要想学的更深更多，可以将通道数增加。但是这将增加计算复杂度。bottleneck design通过1个1*1的卷积，将256维投影回到64维，然后再做通道数不变的卷积，然后再投影回256（将输入和输出的通道数进行匹配，便于进行对比）。等价于先对特征维度降一次维，在降一次维的上面再做一个空间上的东西，然后再投影回去。因此，虽然通道数是之前的4倍，但是在这种设计之下，二者的算法复杂度是差不多的。此外1*1的卷积也可以用于不同channel上特征的融合。

3.3 Resnet如何处理梯度消失

首先对于参数的更新（蓝色部分），我们希望y关于w的导数不会太小，否则即便增大学习率也不能得到提升。

对于传统网络（紫色部分）通过链式求导，g（y）对于y的导数与预测值与真实值之间的差别具有等价关系。假如某时模型预测的已经相对来说比较好了，那么这个值将变得很小，通过相乘就会引起梯度问题进而无法加深网络结构。

对于Resnet（绿色部分），我们看到即便y´对于w的导数很小，通过加法也不会造成梯度消失。这就是Resnet为什么能够训练到1000层的原因。关于1000层以后为什么仍然会出现退化问题，其原因不再是因为结构优化的问题，而是因为网络层级太深太强，而数据集太小太弱，不足以应对如此强大的残差结构，导致了过拟合。

4 总结

Resnet使深层网络更加容易训练，使用残差连接让新的网络至少不会比旧的网络差，并且保证梯度不会消失可以一直跑得动。理论上不加残差网络也能够学到这么一个东西，但是实际上做不到，因为没有引导。而Resnet正是引导整个网络不会走偏，使得它训练出一个更深更好的模型。

参考

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/310065