NLP学习、归并排序、主定理分析、动态规划_哪些nlp相关算法使用了动态规划

机器翻译模型
将句子切分成单词，然后逐个翻译，由排列组合成若干句子，最后经过语言模型，判断哪句更像人话并输出

这种模型的缺点：计算量大， 排列组合数量大，复杂度高

viterb算法将翻译模型和语言模型综合考虑，降低了复杂度
语言模型

概率p的计算：Uni-gram模型，独立计算每个单词的概率
Bi-gram模型：每次考虑前一个单词的概率
Tri-gram模型：每次考虑前两个单词的概率
由此引出n-gram模型
机器学习火的原因就是可以同时考虑前边N个单词
每个单词的概率是要通过模型提前训练好。

马尔科夫假设

以之前的计算概率为基础去计算后边的概率

自然语言处理的四个维度
Morphology层是最基础的层， 是单词层面的技术，比如分词、pos词性标注、NER命名实体识别。这是NLP的基础架构，这里的技术已达到应用的地步
句子结构层：包括句法分析，英文和中文是很不一样的。还有依存分析，确定单词与单词的联系
语义分析是最终目标：包括机器学习，都是为了解决语义

分词

词性分析

命名实体识别：抽取关键词，关心的词

一个领域需要搭建一个命名实体识别器，

依存分析
关系抽取

NLP问题分类

了解这些场景的现状，所处位置，确定项目的可行性，非常重要
明确哪些技术现在能解决
state-of-art要知道

时间复杂度空间复杂度

时间复杂度：运行算法所需要的多长时间
空间复杂度：运行算法占据多大内存

空间复杂度，因为只有两个变量，2个单位的内存空间，这个所需内存空间跟N没有关系，不管我N取100，还是200，我都是需要2个内存空间，所以这里是常数空间复杂度O(1)


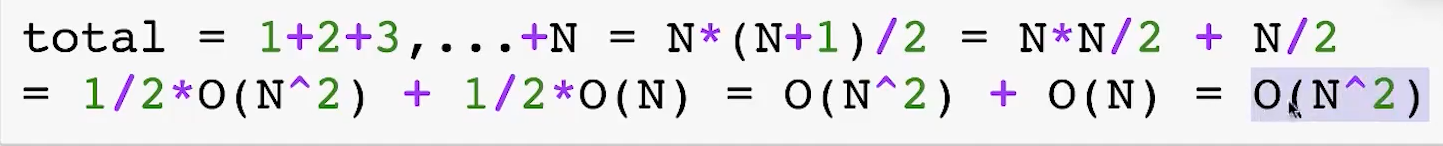
时间复杂度O(n2) 空间O(1)

（LDA算法以后讲）

NLP
基本的算法必须要掌握的，面试肯定问
面试一线的公司有可能问动态规划的问题，需要在纸上写，30分钟写，所以要练习
如果把NLP课程学好，30万没问题，50万需要项目经验
面试会问：过拟合，正则，过拟合，SVM，LDA，HMM等手推
LeetCode有用，每天可以刷一个
AI要理解本质，不能光背
比如只要理解了逻辑回归，能把目标函数写出来，后面的做出来就行了
顶会论文是一个好的点，有一篇ACL就够了
NLP现阶段对学历没要求，但会越来越高，现在缺人才，所以对学历要求不高
一线的公司因为每个岗位报的人太多，所以会直接以学历筛简历
现阶段还达不到真正理解语义

归并排序

子问题中，当分成两部分，每次比较确定一个最小数，比较n次
分成三部分，每次比较两次，比较n次

原问题分了左右两个子问题，最后的归并操作复杂度n
通过递归排序，导出了

计算出T(n) = 2T(n/2) +n
由归并排序递归，引出主定理分析

其实就是比较递归部分和比较部分哪个复杂度更高，就使用哪个

因为f(n) 可以写成

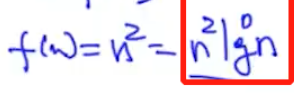
所以T(n)表示为， k=0

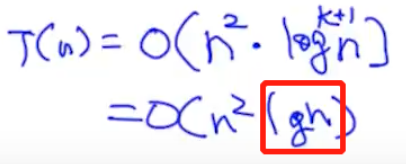
只有相等情况，也就是第二种情况时T(n)稍微复杂一点，其他两种都是哪个复杂度大取哪个

T(n) = O(N^n * logn)

时间复杂度
https://www.jianshu.com/p/f4cca5ce055a

斐波那契数列

计算时间复杂度，用到递归树
最后得到时间复杂度 O(2^n),
递归算法明显的不足是重复计算太多，导致时间复杂度达到了指数级

DP动态规划，解决递归中重复计算的问题

计算空间复杂度
递归当中占几个内存不好看出
当一个函数调用另一个函数时，用到 了栈内存，叫做上下文切换，比如当f(1)执行的时候调用了f(2)，那么f(2)必须先执行完，再来执行f(1)
内存的使用，一种是通过变量的方式使用，另一种是通过上下文切换占用内存
上下文切换占用栈内存，比如计算fib(8),就要计算fub(7),接着fib(6)…fib(1), fib(1)为1，出栈，接着算出fib(2)出栈，一步步运算
知道main函数出栈

当压栈到fib(2),因为已经知道值，所以开始出栈

计算得到一个值，就出栈释放内存，最后发现计算fib(8) 用到的空间就是8个，所以空间复杂度O(n)

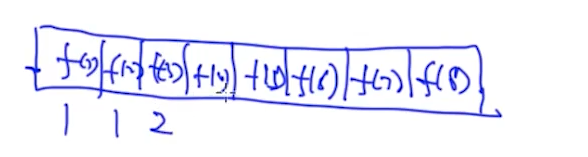
注意：O(n)表示的是复杂度，T(n)表示的是未知函数表达式，这个T是可以用其他字母代替的，只是函数的一个表示

动态规划Dynamic Program：将计算得到的结果用一个数组保存起来，当用到时直接取出P15

动态规划改进：将每次的计算结果保存到数组，时间复杂度由递归的O(2^n)变为O(n)，空间复杂度O(n)

我们每次计算fib(n)都只用到它之前的两个数，所以内存中只保留它前两个数既可，这样空间复杂度由O(n)变为O(1)
当然这里计算feibonaqi数列需要维护的只是之前两次操作，其他有的地方需要维护整个数组

问题分类

我们把一个问题根据时间复杂度分成指数级复杂度和多项式级复杂度
指数级复杂度是不可解决问题，如果对于n比较小的，可以还采用指数级解决问题
如果n比较大，那么只能考虑近似算法，但是不能保证得到精确解
这里第一个要提出近似算法，第二个要指出时间复杂度，最后要给出近似算法算出的近似解离我们想要的最优解的距离

还可以使用量子计算机来解决指数级问题，平时我们使用的计算机是二进制的，量子计算机是多维度计算

我们可以将不可解决的问题归为NP hard， （NPComplete是NPhard的子集）
可以解决的问题，也就是在多项式级复杂度的范围内可以解决的问题，归为P问题

NP问题指的是对于任何一个问题，假设给了你一个解，你去判断这个解到底是不是你想要的。评估这个解的过程是在多项式级复杂度能解决的问题，那么这个问题就是NP问题。

这是一个判断的过程，判断这个解在多项式级能解决，那这个问题就是NP问题。

P问题属于NP问题，因为P问题是多项式级的，那他的判断肯定是有多项式级的解的。

n! n的阶乘是指数级的，阶乘经泰勒展开，近似2^n
百度百科
在计算机领域，一般可以将问题分为可解问题和不可解问题。不可解问题也可以分为两类：一类如停机问题，的确无解；另一类虽然有解，但时间复杂度很高。可解问题也分为多项式问题(Polynomial Problem，P问题)和非确定性多项式问题(NondeterministicPolynomial Problem，NP问题)。
NP问题是指可以在多项式时间内被非确定机解决的问题。通常它们的时间复杂度都是指数变量，如 等。
这里有一个著名的问题一千禧难题之首。是说P问题是否等于NP问题，也即是否所有在非确定机上多项式可解的问题都能在确定机上用多项式时间求解。这表明用NP问题寻找多项式时间表示的算法很困难，或许最后的结论是NP问题根本就不是P问题。