探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（十）

作者：我家自动化 | 2024-04-27 18:42:22

踩

Llama 推理

为了对模型进行推理，需要从Meta的LLaMA 3仓库下载模型的权重。

编写模型推理的代码。在推理模型时，有许多可调参数需要考虑，包括top-k、贪婪搜索/束搜索。为了简单起见，只实现了贪婪搜索。对于束搜索，你可以参考GitHub上LLaMA 3仓库的generation.py文件。

https://github.com/meta-llama/llama3/blob/main/llama/generation.py

以下是您提供的代码段的逐行中文注释：

```python
## 推理部分
from typing import Optional  # 导入可选类型注解
import torch  # 导入PyTorch库
import time  # 导入时间库
import json  # 导入JSON库
from pathlib import Path  # 导入路径库
from sentencepiece import SentencePieceProcessor  # 导入句子片段处理器
from tqdm import tqdm  # 导入进度条库
from model import ModelArgs, Transformer  # 从模型模块导入参数类和Transformer类

class LLaMA:  # 定义LLaMA类

    def __init__(self, model: Transformer, tokenizer: SentencePieceProcessor, model_args: ModelArgs):
        self.model = model  # 初始化模型
        self.tokenizer = tokenizer  # 初始化分词器
        self.args = model_args  # 初始化模型参数

    @staticmethod
    def build(checkpoints_dir: str, tokenizer_path: str, load_model: bool, max_seq_len: int, max_batch_size: int, device: str):
        prev_time = time.time()  # 记录当前时间
        if load_model:  # 如果需要加载模型
            checkpoints = sorted(Path(checkpoints_dir).glob("*.pth"))  # 获取所有检查点文件
            assert len(checkpoints) > 0, "No checkpoints files found"  # 确保检查点文件存在
            chk_path = checkpoints[0]  # 获取最新的检查点路径
            print(f'Loaded checkpoint {chk_path}')  # 打印加载的检查点
            checkpoint = torch.load(chk_path, map_location="cpu")  # 加载检查点
            print(f'Loaded checkpoint in {(time.time() - prev_time):.2f} seconds')  # 打印加载时间
            prev_time = time.time()  # 更新当前时间

        # 加载模型参数
        with open(Path(checkpoints_dir) / "params.json", "r") as f:
            params = json.loads(f.read())
        model_args: ModelArgs = ModelArgs(  # 实例化模型参数
            max_seq_len=max_seq_len,
            max_batch_size=max_batch_size,
            device=device,
            **params  # 展开其他参数
        )
        tokenizer = SentencePieceProcessor()  # 实例化分词器
        tokenizer.load(tokenizer_path)  # 加载分词器模型
        model_args.vocab_size = tokenizer.vocab_size()  # 设置词汇表大小

        # 根据设备类型设置默认的张量类型
        if device == "cuda":
            torch.set_default_tensor_type(torch.cuda.HalfTensor)
        else:
            torch.set_default_tensor_type(torch.BFloat16Tensor)

        model = Transformer(model_args).to(device)  # 实例化Transformer模型并指定设备

        if load_model:  # 如果需要加载模型
            # 从检查点中移除rope.freqs，因为我们是预计算频率
            del checkpoint["rope.freqs"]
            model.load_state_dict(checkpoint, strict=False)  # 加载模型状态字典
            print(f"Loaded state dict in {(time.time() - prev_time):.2f} seconds")  # 打印加载时间

        return LLaMA(model, tokenizer, model_args)  # 返回LLaMA实例

    def text_completion(self, prompts: list[str], temperature: float = 0.6, top_p: float = 0.9, max_gen_len: Optional[int] = None):
        # 如果没有指定最大生成长度，则使用模型参数中的最大序列长度减1
        if max_gen_len is None:
            max_gen_len = self.args.max_seq_len - 1
        # 将每个提示转换为令牌
        prompt_tokens = [self.tokenizer.encode(prompt, out_type=int, add_bos=True, add_eos=False) for prompt in prompts]
        # 确保批量大小不是太大
        batch_size = len(prompt_tokens)
        assert batch_size <= self.args.max_batch_size, f"Batch size {batch_size} is too large"
        max_prompt_len = max(len(prompt) for prompt in prompt_tokens)
        # 确保提示长度不大于最大序列长度
        assert max_prompt_len < self.args.max_seq_len, f"Prompt length {max_prompt_len} is too large"
        total_len = min(self.args.max_seq_len, max_gen_len + max_prompt_len)

        # 创建一个列表，用于包含生成的令牌以及初始提示令牌
        pad_id = self.tokenizer.pad_id()
        tokens = torch.full((batch_size, total_len), pad_id, dtype=torch.long, device=self.args.device)
        for k, t in enumerate(prompt_tokens):
            tokens[k, :len(t)] = torch.tensor(t, dtype=torch.long, device=self.args.device)

        eos_reached = torch.tensor([False] * batch_size, device=self.args.device)
        # 如果令牌是提示令牌，则为True，否则为False
        prompt_tokens_mask = tokens != pad_id  
        for cur_pos in tqdm(range(1, total_len), desc='Generating tokens'):
            with torch.no_grad():  # 不计算梯度
                logits = self.model.forward(tokens[:, cur_pos-1:cur_pos], cur_pos)
            if temperature > 0:  # 如果设置了温度参数
                # 在softmax之前应用温度
                probs = torch.softmax(logits[:, -1] / temperature, dim=-1)
                next_token = self._sample_top_p(probs, top_p)
            else:  # 如果温度参数为0，则贪婪选择概率最大的令牌
                next_token = torch.argmax(logits[:, -1], dim=-1)

            next_token = next_token.reshape(-1)
            # 只有在位置是填充令牌时才替换令牌
            next_token = torch.where(prompt_tokens_mask[:, cur_pos], tokens[:, cur_pos], next_token)
            tokens[:, cur_pos] = next_token
            # 如果填充位置找到了EOS令牌，则EOS已到达
            eos_reached |= (~prompt_tokens_mask[:, cur_pos]) & (next_token == self.tokenizer.eos_id())
            if all(eos_reached):  # 如果所有序列都已到达EOS，则跳出循环
                break

        out_tokens = []
        out_text = []
        for prompt_index, current_prompt_tokens in enumerate(tokens.tolist()):
            # 如果存在EOS令牌，则剪切到EOS令牌
            if self.tokenizer.eos_id() in current_prompt_tokens:
                eos_idx = current_prompt_tokens.index(self.tokenizer.eos_id())
                current_prompt_tokens = current_prompt_tokens[:eos_idx]
            out_tokens.append(current_prompt_tokens)
            out_text.append(self.tokenizer.decode(current_prompt_tokens))

        return (out_tokens, out_text)  # 返回生成的令牌和文本

    def _sample_top_p(self, probs, p):
        # 对概率进行排序
        probs_sort, probs_idx = torch.sort(probs, dim=-1, descending=True)
        # 计算累积概率
        probs_sum = torch.cumsum(probs_sort, dim=-1)
        # 创建一个掩码，当累积概率超过阈值p时为True
        mask = probs_sum - probs_sort > p
        probs_sort[mask] = 0.0  # 将超过阈值的概率设置为0
        probs_sort.div_(probs_sort.sum(dim=-1, keepdim=True))  # 重新归一化概率
        next_token = torch.multinomial(probs_sort, num_samples=1)  # 从概率中采样下一个令牌
        next_token = torch.gather(probs_idx, -1, next_token)  # 根据采样的索引获取对应的令牌
        return next_token  # 返回采样的下一个令牌

if __name__ == '__main__':
    import os  # 导入操作系统库
    torch.manual_seed(0)  # 设置随机种子以确保结果的可复现性
    prompts = [  # 定义提示列表
        # 少量样本提示
        """Translate English to kananda:
        water : ನೀರು
        land : ಭೂಮಿ
        dusk : ಸಂಜೆ
        dawn : ಬೆಳಗುವಿಕೆ
        milk : ಹಾಲು""",
        # 零样本提示
        """Tell me if the following person is actually a real person or a fictional character:
        Name : Vignesh 
        Decision:
        """
    ]
    # 检查CUDA是否可用
    allow_cuda = True if 'CUDA_VISIBLE_DEVICES' in os.environ else False
    device = 'cuda' if torch.cuda.is_available() and allow_cuda else 'cpu'  # 根据CUDA的可用性选择设备

    # 构建LLaMA模型
    model = LLaMA.build(
        checkpoints_dir='Meta-Llama-3-8B/',
        tokenizer_path='Meta-Llama-3-8B/tokenizer.model',
        load_model=True,
        max_seq_len=1024,
        max_batch_size=len(prompts),
        device=device
    )

    print('ALL OK')  # 打印模型构建成功的消息

    # 对模型进行推理
    print("Inferenceing the model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163

附录：
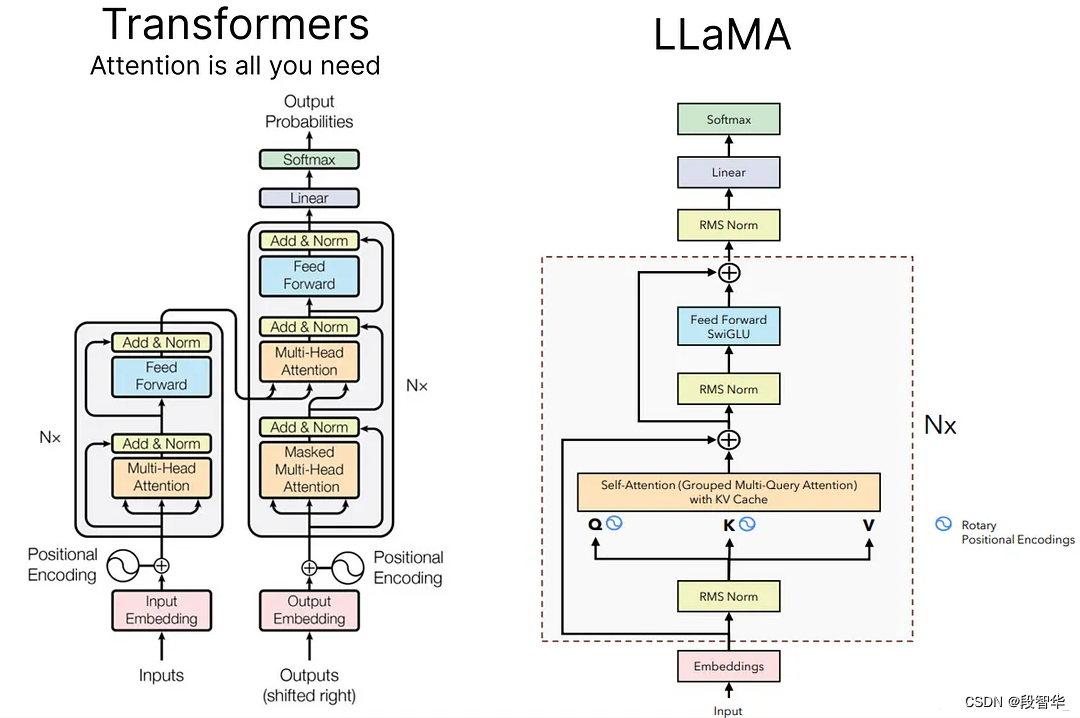
在这里插入图片描述

使用 PyTorch 从头开始构建 Llama2 架构:
所有模型都是从头开始构建的，包括 GQA（分组查询注意）、RoPE（旋转位置嵌入）、RMS Norm、前馈块、编码器（因为这仅用于推理模型）、SwiGLU（激活函数）

https://github.com/viai957/llama-inference

## LLaMA - Large Language Model with Attention

import torch
import torch.nn.functional as F
import math
import torch.nn as nn
from tqdm import tqdm
from dataclasses import dataclass
from typing import Optional


@dataclass
class ModelArgs:
    dim: int = 4096
    n_layers: int = 32
    n_heads: int = 32 # Number of heads for the queries
    n_kv_heads: Optional[int] = None # Number of heads for the keys and values. If None, defaults to n_heads
    vocab_size: int = -1 # This will be set when we load the tokenizer
    multiple_of: int = 256 
    ffn_dim_multiplier: Optional[float] = None # If None, defaults to 4.0
    norm_eps: float = 1e-5
    
    # Needed for KV cache
    max_batch_size: int = 32
    max_seq_len: int = 2048

    device: str = None

def precomputed_theta_pos_frequencies(head_dim: int, seq_len: int, device: str, theta: float = 10000.0):
    # As written in the paper, the dimentions o the embedding must be even
    assert head_dim % 2 == 0, "The head_dim must be even"
    # Built the theta parameters
    # According to the formula theta_i = 10000 ^ (-2(i-1)/dim) for i = [1,2,3,..dim/2]
    # Shape: (head_dim / 2)
    theta_numerator = torch.arange(0, head_dim, 2).float()
    # Shape : (head_dim / 2)
    theta = 1.0 / (theta ** (theta_numerator / head_dim)).to(device)
    # Construct the positions (the "m" parameter)
    # shape: (seq_len)
    m = torch.arange(seq_len, device=device)
    # multiply each theta by each position using the outer product
    # shape : (seq_len) outer_product * (head_dim / 2) -> (seq_len, head_dim / 2)
    freq = torch.outer(m, theta).float()
    # we can computer complex numbers in the polar form c = R * exp(i * m * theta), where R = 1 as follow
    # shape: (seq_len, head_dim/2) -> (seq-len, head_dim/2)
    freq_complex = torch.polar(torch.ones_like(freq), freq)
    return freq_complex

def apply_rotary_embeddings(x: torch.Tensor, freq_complex: torch.Tensor, device: str):
    # We transform the each subsequent pair of tokens into a pair of complex numbers
    # shape : (B, seq_len, head_dim) -> (B, seq_len, h, head_dim / 2)
    x_complex = torch.view_as_complex(x.float().reshape(*x.shape[:-1], -1, 2))
    # shape : (seq_len, head_dim / 2) -> (1, seq_len, 1, head_dim / 2)
    freq_complex = freq_complex.unsqueeze(0).unsqueeze(2)
    # shape : (B, seq_len, h, head_dim / 2) * (1, seq_len, 1, head_dim / 2) = (B, seq_len, h, head_dim / 2)
    x_rotate = x_complex * freq_complex
    # (B, seq_len, h, head_dim / 2) -> (B, seq_len, h, head_dim/2 ,2)
    x_out = torch.view_as_real(x_rotate)
    # (B, seq_len, h, head_dim/2, 2) -> (B, seq_len, h * head_dim / 2 * 2)
    x_out = x_out.reshape(*x.shape)
    return x_out.type_as(x).to(device)

def repeat_kv(x: torch.Tensor, n_rep: int)-> torch.Tensor:
    batch_size, seq_len, n_kv_heads, head_dim = x.shape
    if n_rep == 1:
        return x
    else:
        return (
            # (B, seq_len, n_kv_heads, 1, head_dim)
            x[:, :, :, None, :]
            .expand(batch_size, seq_len, n_kv_heads, n_rep, head_dim)
            .reshape(batch_size, seq_len, n_kv_heads * n_rep, head_dim)
        )

class SelfAttention(nn.Module): 
    def  __init__(self, args: ModelArgs):
        super().__init__()
        self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
        # Indicates the number of heads for the queries
        self.n_heads_q = args.n_heads
        # Indiates how many times the heads of keys and value should be repeated to match the head of the Query
        self.n_rep = self.n_heads_q // self.n_kv_heads
        # Indicates the dimentiona of each head
        self.head_dim = args.dim // args.n_heads

        self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
        self.wk = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)
        self.wv = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)
        self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)

        self.cache_k = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim))
        self.cache_v = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim))

    def forward(self, x: torch.Tensor, start_pos: int, freq_complex: torch.Tensor):
        batch_size, seq_len, _ = x.shape #(B, 1, dim)
        # Apply the wq, wk, wv matrices to query, key and value
        # (B, 1, dim) -> (B, 1, H_q * head_dim)
        xq = self.wq(x)
        # (B, 1, dim) -> (B, 1, H_kv * head_dim)
        xk = self.wk(x)
        xv = self.wv(x)

        # (B, 1, H_q * head_dim) -> (B, 1, H_q, head_dim)
        xq = xq.view(batch_size, seq_len, self.n_heads_q, self.head_dim)
        xk = xk.view(batch_size, seq_len, self.n_kv_heads, self.head_dim)
        # (B, 1, H_kv * head_dim) -> (B, 1, H_kv, head_dim)
        xv = xv.view(batch_size, seq_len, self.n_kv_heads, self.head_dim)

        # Apply the rotary embeddings to the keys and values
        # Does not chnage the shape of the tensor
        # (B, 1, H_kv, head_dim) -> (B, 1, H_kv, head_dim)
        xq = apply_rotary_embeddings(xq, freq_complex, device=x.device)
        xk = apply_rotary_embeddings(xk, freq_complex, device=x.device)

        # Replace the enty in the cache for this token
        self.cache_k[:batch_size, start_pos:start_pos + seq_len] = xk
        self.cache_v[:batch_size, start_pos:start_pos + seq_len] = xv

        # Retrive all the cached keys and values so far
        # (B, seq_len_kv, H_kv, head_dim)
        keys = self.cache_k[:batch_size, 0:start_pos + seq_len]
        values = self.cache_v[:batch_size, 0:start_pos+seq_len] 

        # Repeat the heads of the K and V to reach the number of heads of the queries
        keys = repeat_kv(keys, self.n_rep)
        values = repeat_kv(values, self.n_rep)

        # (B, 1, h_q, head_dim) --> (b, h_q, 1, head_dim)
        xq = xq.transpose(1, 2)
        keys = keys.transpose(1, 2)
        values = values.transpose(1, 2)

        # (B, h_q, 1, head_dim) @ (B, h_kv, seq_len-kv, head_dim) -> (B, h_q, 1, seq_len-kv)
        scores = torch.matmul(xq, keys.transpose(2,3)) / math.sqrt(self.head_dim)
        scores = F.softmax(scores.float(), dim=-1).type_as(xq)

        # (B, h_q, 1, seq_len) @ (B, h_q, seq_len-kv, head_dim) --> (b, h-q, q, head_dim)
        output = torch.matmul(scores, values)

        # (B, h_q, 1, head_dim) -> (B, 1, h_q, head_dim) -> ()
        output = (output.transpose(1,2).contiguous().view(batch_size, seq_len, -1))
        return self.wo(output) # (B, 1, dim) -> (B, 1, dim)

class FeedForward(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()
        # Assuming 'hidden_dim' is calculated as per your specifications
        hidden_dim = 4 * args.dim
        hidden_dim = int(2 * hidden_dim / 3)  # Applying your specific transformation
        if args.ffn_dim_multiplier is not None:
            hidden_dim = int(args.ffn_dim_multiplier * hidden_dim)
        #hidden_dim = int(2 * hidden_dim / 3)  # Applying your specific transformation
        hidden_dim = args.multiple_of * ((hidden_dim + args.multiple_of - 1) // args.multiple_of)

        self.w1 = nn.Linear(args.dim, hidden_dim, bias=False)
        self.w2 = nn.Linear(hidden_dim, args.dim, bias=False)  # This layer seems to be missing in your original setup
        self.w3 = nn.Linear(args.dim, hidden_dim, bias=False)  # Corrected to match checkpoint

    def forward(self, x: torch.Tensor):
        swish = F.silu(self.w1(x))  # Apply first transformation
        x_V = self.w3(x) 
        x = swish * x_V        # Apply contraction to original dimension
        x = self.w2(x)  # Apply optional additional transformation
        return x

class EncoderBlock(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.n_heads = args.n_heads
        self.dim = args.dim
        self.head_dim = args.dim // args.n_heads

        self.attention = SelfAttention(args)
        self.feed_forward = FeedForward(args)

        # normalize BEFORE the self attention
        self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)
        # Normalization BEFORE the feed forward
        self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)

    def forward(self, x: torch.Tensor, start_pos: int, freqs_complex: torch.Tensor):
        # (B, seq_len, dim) + (B, seq_len, dim) -> (B, seq_len, dim)
        h = x + self.attention.forward(self.attention_norm(x), start_pos, freqs_complex)
        out = h + self.feed_forward.forward(self.ffn_norm(h))
        return out
    
class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        self.eps = eps
        # The gamma parameter
        self.weight = nn.Parameter(torch.ones(dim))

    def _norm(self, x: torch.Tensor):
        # (B, seq_len, dim) -> (B, seq_len, 1)
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x: torch.Tensor):
        # dim : (B, seq_len, dim) -> (B, seq_len, dim)
        return self.weight * self._norm(x.float()).type_as(x)

class Transformer(nn.Module):
    
    def __init__(self, args: ModelArgs) -> None:
        super().__init__()

        assert args.vocab_size != -1, "Vocab size must be set"

        self.args = args
        self.vocab_size = args.vocab_size
        self.n_layers = args.n_layers
        self.tok_embeddings = nn.Embedding(self.vocab_size, args.dim)

        self.layers = nn.ModuleList()
        for _ in range(args.n_layers):
            self.layers.append(EncoderBlock(args))

        self.norm = RMSNorm(args.dim, eps=args.norm_eps)
        self.output = nn.Linear(args.dim, self.vocab_size, bias=False)

        # To precompute the frequencies of the Rotary Positional Encodings
        self.freqs_complex = precomputed_theta_pos_frequencies(self.args.dim // self.args.n_heads, self.args.max_seq_len * 2, device=self.args.device)

    def forward(self, tokens: torch.Tensor, start_pos: int):
        # (B, seq_len)
        batch_size, seq_len = tokens.shape
        assert seq_len == 1, "Only one token at a time can be processed"
  
        # (B, seq_len) -> (B, seq_len, dim)
        h = self.tok_embeddings(tokens)

        # Retrive the pairs (m, theta) corresponding to the positions [start_pos, start_pos + seq_len]
        freqs_complex = self.freqs_complex[start_pos:start_pos + seq_len]

        # Consecutively apply all the encoder layers
        for layer in self.layers:
            h = layer(h, start_pos, freqs_complex)
        h =  self.norm(h)
        output = self.output(h).float()
        return output
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240

系列博客

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（一）Llama3 模型架构
https://duanzhihua.blog.csdn.net/article/details/138208650
探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（二）RoPE位置编码
https://duanzhihua.blog.csdn.net/article/details/138212328

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（三）KV缓存
https://duanzhihua.blog.csdn.net/article/details/138213306

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（四）分组多查询注意力
https://duanzhihua.blog.csdn.net/article/details/138216050
探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（五）RMS 均方根归一化
https://duanzhihua.blog.csdn.net/article/details/138216630

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（六）SwiGLU 激活函数
https://duanzhihua.blog.csdn.net/article/details/138217261
探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（七）前馈神经网络
https://duanzhihua.blog.csdn.net/article/details/138218095

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（八）Transformer块
https://duanzhihua.blog.csdn.net/article/details/138218614

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（九）Llama Transformer架构
https://duanzhihua.blog.csdn.net/article/details/138219242

立即解锁无限学习的大门，快速报名，开启知识的奇妙旅程！

在这里插入图片描述

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/498149