排序2——C语言

交换排序的基本思想：所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。

交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

1. 冒泡排序

冒泡排序一定是大家学习的编程路上接触的第一个排序，它效率并不高，但是还是需要介绍的。

思想：对待排序数据两两比较，将键值大的换到后面，一趟排序完成后，最大的数就换到末尾了。

//冒泡排序
//复杂度O(N^2)
void BubbleSort(int* array, int numsArr)
{
	//冒numsArr-1趟
	for (int i = 0; i < numsArr - 1; i++)
	{
		
		bool flag = true;
		//一趟比较numsArr-i-1次
		for (int j = 1; j < numsArr - i; j++)
		{
			if (array[j - 1] > array[j])
			{
				swap(&array[j - 1], &array[j]);
                flag = false;
			}
		}
		//满足条件说明有序
		if (flag == true)
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

这里做了一个优化，即如果在一趟排序内，没有一次交换，说明序列已经有序，就不用再继续排序了。

2. 快速排序

重点介绍快速排序，这里介绍四种方法，大家可以选择好理解的方法。

2.1 递归法1

思想：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后对左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

什么意思呢，通俗点说就是，先选一个值，排完一趟后，小于这个值的数都这个值的左边，大于这个值的数都再这个值的右边，等于这个值出现在左右都可以。然后对左右两块区间重复这个过程，直到全部排好。

假设排序{6，4，2，1，5，8，7，3，9}那么过程如下图

这样有几个注意点：

1. 我们需要改变数组内的顺序，因此需要保存的是key值的下标
2. 重复这个过程，势必用到递归，那么需要找返回条件。（区间内只有一个数或者区间不存在）
3. key值的选取，默认为第一个时，会有缺陷，当数组是有序或者接近有序时，这个排序的时间复杂度就变为O(N^2)了，需要对key值的选取进行更改。这里的方法是三数取中，三数（首元素，尾元素，中间元素）

代码如下

void swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//三数取中
int MidNum(int* array, int left, int right)
{
	int mid = (left + right) / 2;
	//找到最大的数
	int max_ = max(max(array[left], array[mid]), array[right]);
	//找第二大的数
	if (max_ == array[left])
	{
		return max(mid, right);
	}
	else
	{
		if (max_ == array[mid])
		{
			return max(left, right);
		}
		else
		{
			return max(left, mid);
		}
	}
}

//快速排序
//复杂度O(N*logN)
//最坏：有序或者接近有序O(N^2)
//hoare版本
void QuickSort1(int* array, int left, int right)//数组左右闭区间，[left,right]
{
	//数组只有一共值或者数组不存在
	if (left >= right)
	{
		return;
	}
	//基准值下标
	int keyIndex = MidNum(array,left,right);
	int begin = left, end = right;
	while (left < right)
	{
		//右边找小
		while (left < right && array[right] >= array[keyIndex])
		{
			right--;
		}
		//左边找大
		while (left < right && array[left] <= array[keyIndex])
		{
			left++;
		}
		//交换
		swap(&array[left], &array[right]);
	}
	//交换基准值和相遇位置处
	swap(&array[left], &array[keyIndex]);
	keyIndex = left;

	//递归[ begin(left),keyIndex-1 ] keyIndex [ keyIndex+1,end(right) ]
	QuickSort1(array, begin, keyIndex - 1);
	QuickSort1(array, keyIndex + 1, end);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

2.2 前后指针法

思路：有两个指针，cur和prev，cur找小于基准值的数据，找到后和 ++prev 位置的数据交换。循环直到cur走完整个序列，基准值和prev位置的数据再进行交换即可。对左右子区间做相同操作就能完成排序。

这里举例排序6 1 9 5 3 2 8 4的第一趟。

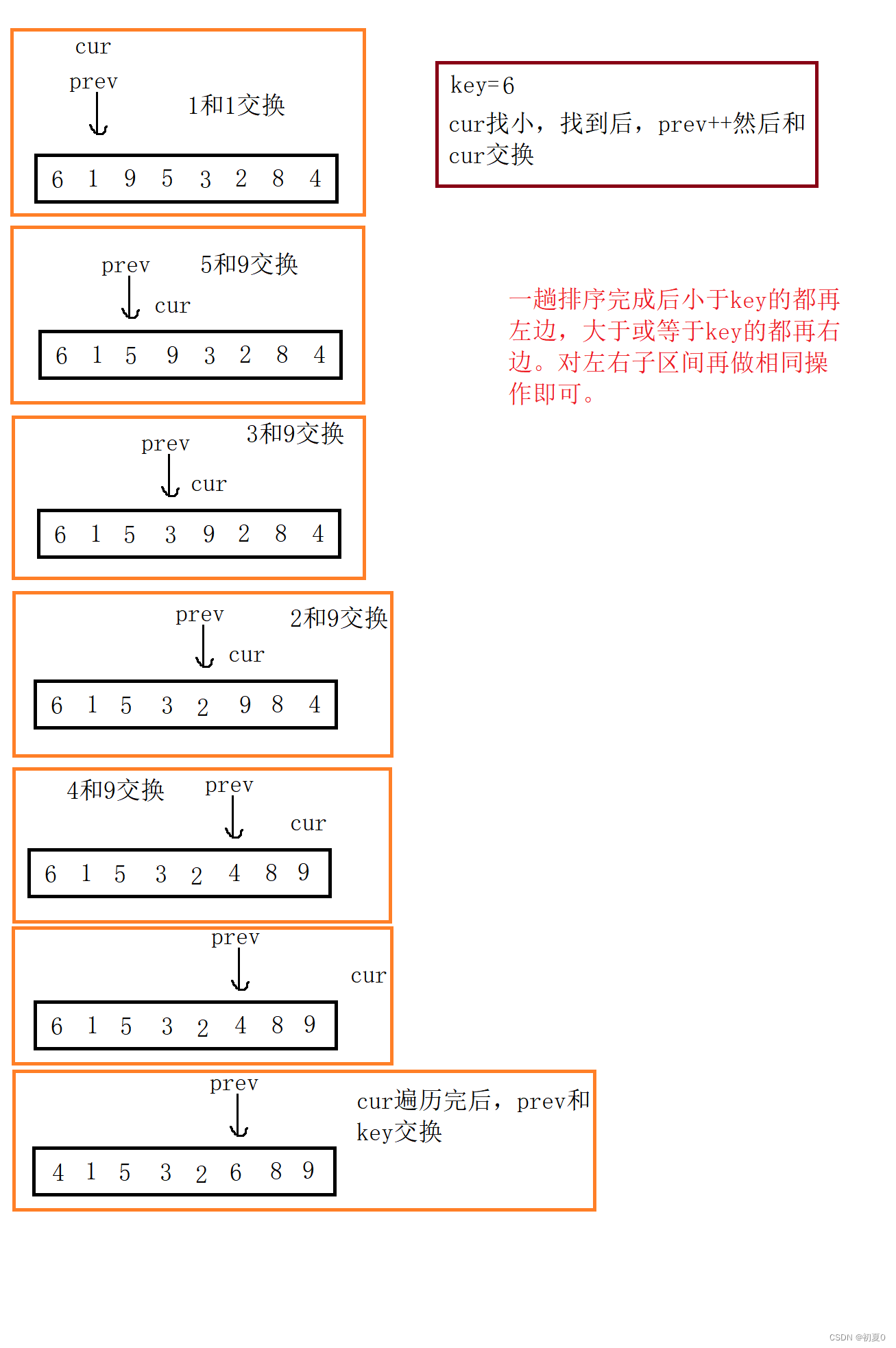
这个方法的prev指针就好像一个漏网，把数据大的网住，一步步拉向后面。

完整代码如下

//前后指针法
void QuickSort2(int* array, int left, int right)
{
	if (left >= right)
		return;

	int keyi = left;
	int prev = left;
	int cur = prev + 1;

	//cur找小，找到和prev交换
	while (cur <= right)
	{
		if (array[cur] < array[keyi])
		{
			++prev;
			swap(&array[prev], &array[cur]);
		}
		++cur;
	}
	swap(&array[prev], &array[keyi]);
	keyi = prev;
	//递归基准值两边
	QuickSort2(array, left, keyi - 1);
	QuickSort2(array, keyi + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

swap函数同上，这个方法是我认为比较好理解的，需要注意的点也没有那么多。

2.3 挖坑法

这个方法和法1很类似，但是更形象

思路：保留第一个数据，第一个位置就空出来了形成一个坑。右边（end）先走找小，找到后，放到坑内，形成一个新的坑。左边（begin）再走找大，找到后放到坑内，又形成一个新的坑，循环。左右指标相遇后，把保留的数据放在相遇位置即可，第一趟的排序就完成了，然后对左右子区间执行相同的操作。文字不好叙述，直接上图。还是排序 6 1 9 5 3 2 8 4 这组数据。

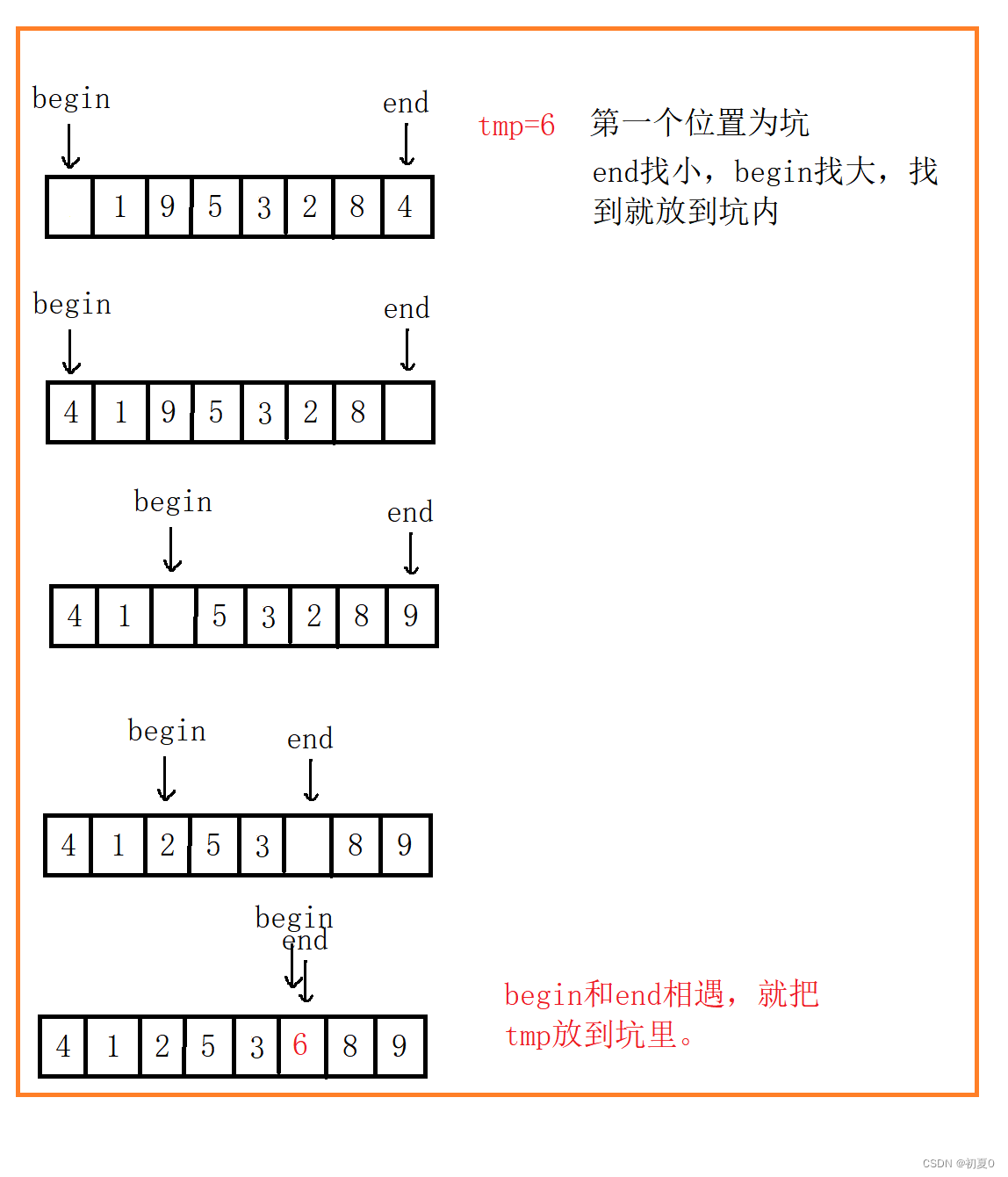
这样第一趟的排序就完成了，对左右子区间再完成相同的操作即可。

完整代码如下

//挖坑法
void QuickSort3(int* array, int left, int right)
{
	if (left >= right)
	{
		return;
	}
	int tmp = array[left];
	int keyIndex = left;
	int begin = left, end = right;
	while (begin < end)           //{5,1,2,4,3,6,9,7,10,8};
	{
		while (begin<end)
		{
			//右边找小
			if (array[end] < tmp)
			{
				array[begin] = array[end];
				break;
			}
			else
			{
				--end;
			}
		}
		while (begin < end)
		{
			//左边找大
			if (array[begin] > tmp)
			{
				array[end] = array[begin];
				break;
			}
			else
			{
				++begin;
			}
		}
	}
	array[begin] = tmp;

	keyIndex = begin;
	//递归左右子区间
	QuickSort3(array, left, keyIndex - 1);
	QuickSort3(array, keyIndex + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

前后指针法和挖坑法中，对于基准值的选取，依旧可以采用三数取中，大家可以自行修改完善代码。这三种方法都是递归，最后一种为非递归的方法。需要借助一个栈的数据结构。

2.4 快排非递归

思路：入栈整个区间（两个数，左右区间下标），再出栈完成对序列的第一趟排序，再入栈左右子区间，出栈子区间，完成排序。栈为空后，说明序列排序完成。

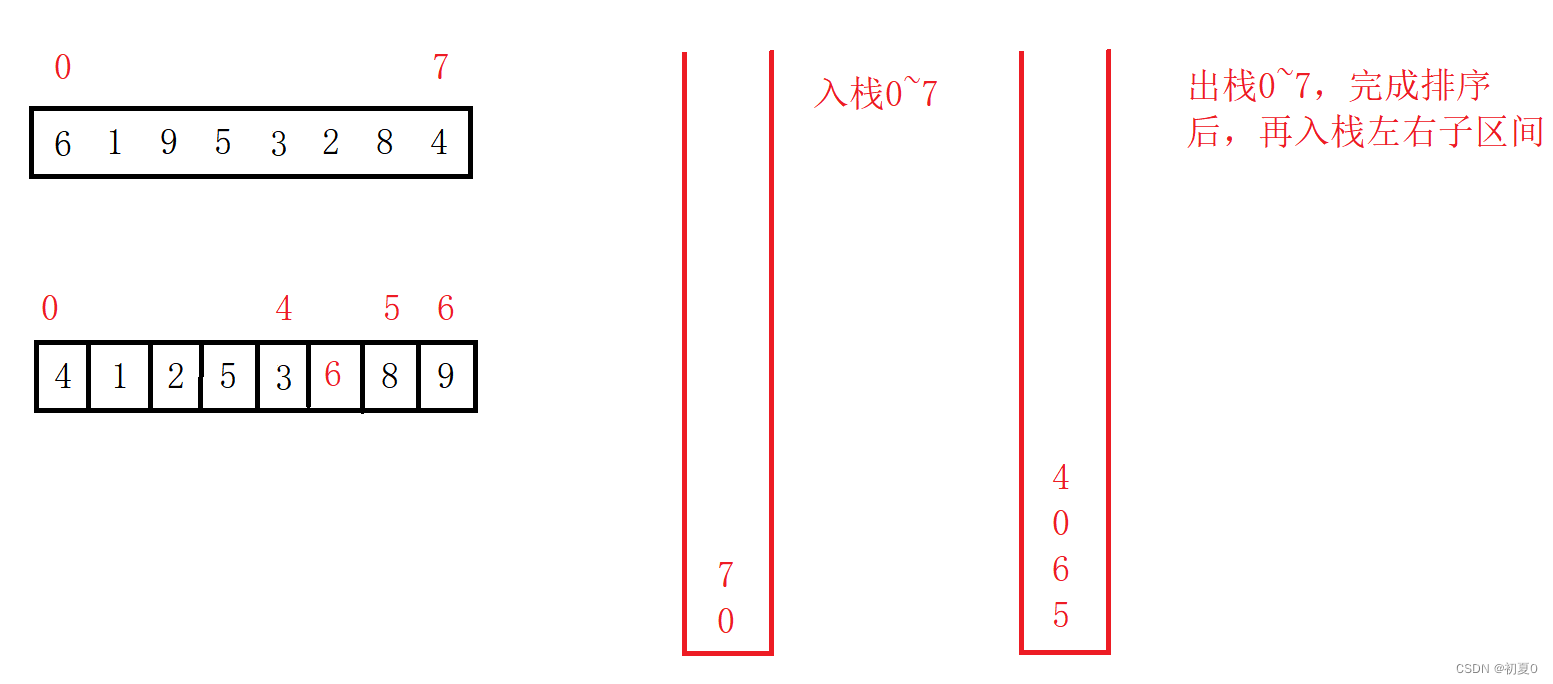
这个方法是利用了数据结构的栈来存储下标，进而完成对不同区间的快排。
对于栈的数据结构，之前已经写过了，这里可以直接拿来使用。

//快排非递归
void QuickSortNonRe(int* array, int left, int right)
{
	STNode s;
	StackInit(&s);
	StackPush(&s, left);
	StackPush(&s, right);
	while (!StackEmpty(&s))
	{
		int end = FindTop(&s);
		StackPop(&s);
		int begin = FindTop(&s);
		StackPop(&s);

		if (end - begin <= 1)
		{
			continue;
		}

		int keyi = begin;
		int prev = begin;
		int cur = begin + 1;

		//cur找小，找到和prev交换
		while (cur <= end)
		{
			if (array[cur] < array[keyi])
			{
				++prev;
				swap(&array[prev], &array[cur]);
			}
			++cur;
		}
		swap(&array[prev], &array[keyi]);
		keyi = prev;

		StackPush(&s, keyi + 1);
		StackPush(&s, end);

		StackPush(&s, begin);
		StackPush(&s, keyi - 1);

	}

	StackDestroy(&s);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

快速排序的时间复杂度为O（N*logN）

3. 代码和性能测试

void test()
{
	srand(time(0));
	int n = 1000;

	int* a1 =(int*)malloc(sizeof(int) * n);
	int* a2 =(int*)malloc(sizeof(int) * n);
	int* a3 =(int*)malloc(sizeof(int) * n);
	int* a4 =(int*)malloc(sizeof(int) * n);
	int* a5 =(int*)malloc(sizeof(int) * n);
	int* a6 =(int*)malloc(sizeof(int) * n);
	int* a7 =(int*)malloc(sizeof(int) * n);
	int* a8 =(int*)malloc(sizeof(int) * n);
	int* a9 =(int*)malloc(sizeof(int) * n);
	int* a10 =(int*)malloc(sizeof(int) * n);
	int* a11 =(int*)malloc(sizeof(int) * n);

	for (int i = 0; i < n; i++)
	{
		a1[i] = rand() % n;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
		a8[i] = a1[i];
		a9[i] = a1[i];
		a10[i] = a1[i];
		a11[i] = a1[i];
	}

	printf("排序%d个数所用的时间(ms)\n",n);

	int begin1 = clock();
	ShellSort(a1, n);
	int end1 = clock();

	int begin2 = clock();
	HeapSort(a2, n);
	int end2 = clock();

	int begin3 = clock();
	QuickSort1(a3, 0, n - 1);
	int end3 = clock();

	int begin4 = clock();
	QuickSort2(a4, 0, n - 1);
	int end4 = clock();

	int begin5 = clock();
	MergeSort(a5, n);
	int end5 = clock();

	int begin6 = clock();
	MergeSortNonRe(a6, n);
	int end6 = clock();

	int begin7 = clock();
	QuickSort3(a7, 0, n - 1);
	int end7 = clock();

	int begin8 = clock();
	QuickSortNonRe(a8, 0, n - 1);
	int end8 = clock();

	int begin9 = clock();
	InsertSort(a9, n);
	int end9 = clock();

	int begin10 = clock();
	SelectSort(a10, n);
	int end10 = clock();

	int begin11 = clock();
	BubbleSort(a11, n);
	int end11 = clock();


	printf("希尔排序:%d", end1-begin1);
	printf("\n堆排序:%d", end2 - begin2);
	printf("\n快速排序1(hoare版本):%d", end3 - begin3);
	printf("\n快速排序2(前后指针法):%d", end4 - begin4);
	printf("\n快速排序3(挖坑法):%d", end7 - begin7);
	printf("\n快速排序4(非递归):%d", end8 - begin8);
	/*printf("\n归并排序:%d", end5 - begin5);
	printf("\n归并排序(非递归):%d", end6 - begin6);*/
	printf("\n直接插入排序:%d", end9 - begin9);
	printf("\n直接选择排序:%d", end10 - begin10);
	printf("\n冒泡排序:%d", end11 - begin11);

}

int main()
{
	test();
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99

用上述方法，完成对多个数组进行相同的初始化，我们看一下这些排序的性能差别。
之前的排序也加入测试，对比一下。测试性能时，我们要在release版本下测试。

先对比1000个数据所用的时间，单位是毫秒（ms）

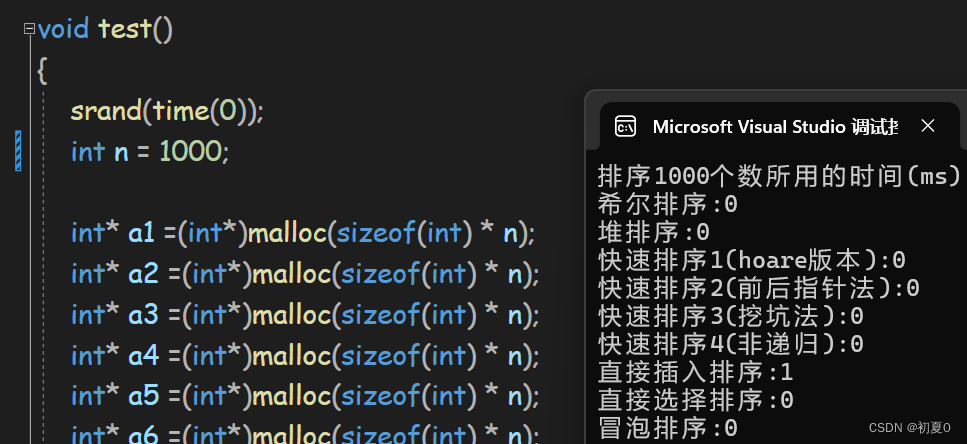
可以看到，数据量为1000时，都很快。这里的0不是指0毫秒，而是指所用的时间小于1毫秒。

数据量扩大十倍后（一万）

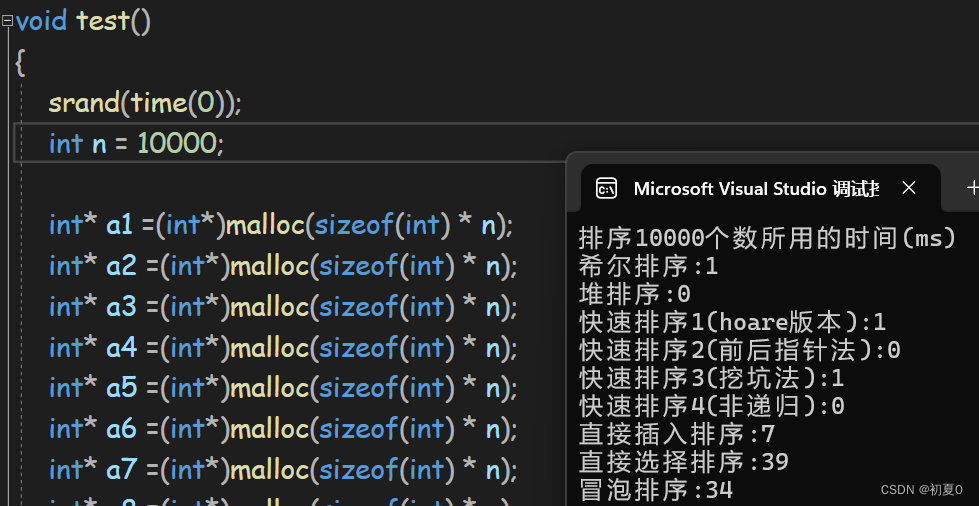
数据量再扩大十倍（十万）

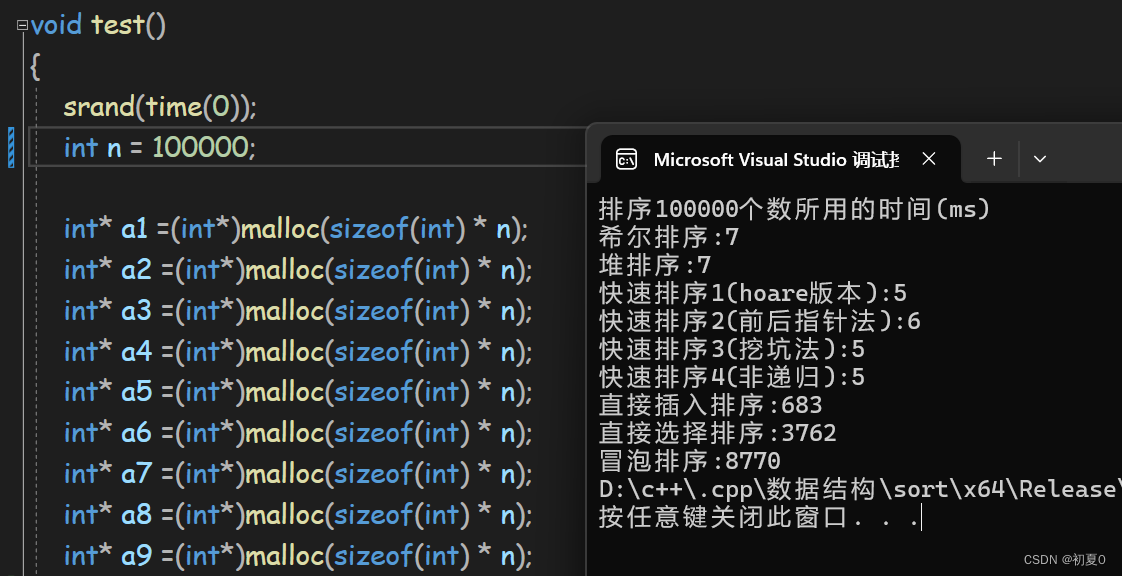
当数据量为十万时，后三个排序已经开始吃力了，和前面的对比速度差了一百多倍 。后续就不测试它们了，这里直接把数据量加到一千万。

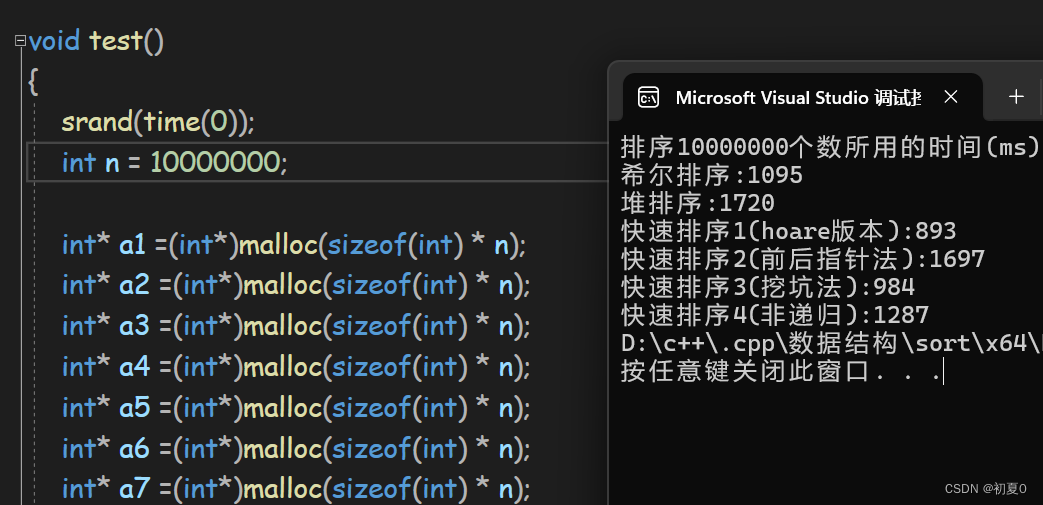
可以看到，复杂度为O（N^2）和O（N*logN）的排序算法时间差异还是蛮大的。

关于快排就介绍到这里了，下篇介绍归并排序、计数排序以及这些排序算法的稳定性。