排序FollowUp

FollowUp

插入排序

直接插入排序

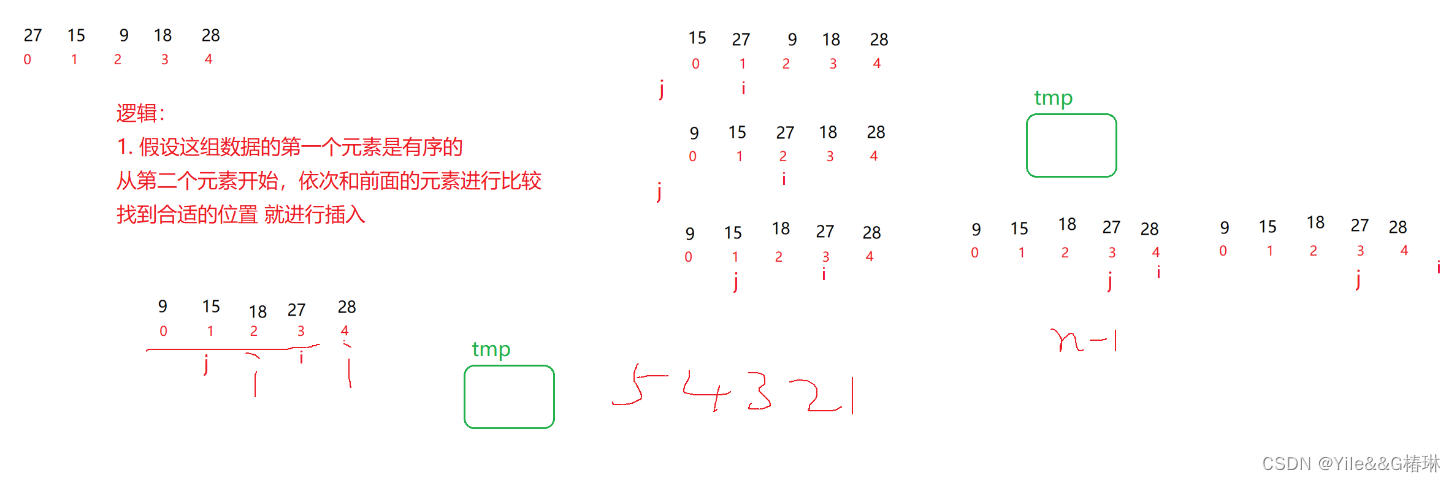
时间复杂度:
最坏情况下:0(n^2)
最好情况下:0(n)当数据越有序 排序越快

适用于: 待排序序列 已经基本上趋于有序了!
空间复杂度:0(1)
稳定性:稳定的

   public static void insertSort(int[] array){
        for (int i = 1; i < array.length; i++) {
            int tmp = array[i];
            int j = i - 1;
            for (; j >= 0 ; j--) {
                    //这里加不加等号 和稳定有关系
                    // 但是:本身就是一个稳定的排序 可以实现为不稳定的排序
                    // 但是 本身就是一个不稳定的排序 是不可能变成一个稳定的排序的
                if(array[j] > tmp){
                    array[j + 1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }

 希尔排序（缩小增量排序）

重点是最后还是会把整体作一组来直接插入排序

  public static void shellSort(int[] array){
        int gap = array.length;
        while(gap > 1){
            shell(array,gap);
            gap /= 2;
        }
    }
    public static void shell(int[] array, int gap){
        for (int i = gap; i < array.length; i++) {
            int tmp = array[i];
            int j = i - gap;
            for (;j >= 0; j -= gap) {
                if(array[j] > tmp){
                    array[j+gap] = array[j];
                }else {
                    break;
                }
 
            }
            array[j+gap] = tmp;
        }
    }

 选择排序

直接选择排序

在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
在剩余的array[i]--array[n-2]（array[i+1]--array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

    public static void selectSort(int[] array){
        for (int i = 0; i < array.length; i++) {
            int mixIndex = i;
            for (int j = i+1; j < array.length; j++) {
                if(array[mixIndex] > array[j]){
                    mixIndex = j;
                }
            }
            int tmp = array[i];
            array[i] = array[mixIndex];
            array[mixIndex] = tmp;
        }
    }

【直接选择排序的特性总结】
1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

双向选择排序：

 public static void selectSort2(int[] array){
 
        int left = 0;
        int right = array.length-1;
        while(left < right){
            int minIndex = left;
            int maxIndex = left;
            for (int i = left+1; i < right; i++) {
                if(array[i] > array[maxIndex]){
                    maxIndex = i;
                }
                if(array[i] < array[minIndex]){
                    minIndex = i;
                }
                swap(array,left,minIndex);
                //防止最大的是在第一个的时候
                if(maxIndex == left){
                    maxIndex = minIndex;
                }
                swap(array,right,maxIndex);
                left++;
                right--;
 
            }
        }
    }

堆排序

具体的思路在PriorityQueue（一）——用堆实现优先级队列

    public static void heapSort(int[] array){
        creatHeap(array);
        int end = array.length-1;
        while(end > 0){
           swap(array,0,end);
           siftDown(array,0,end);
           end--;
        }
    }
 
    private static void creatHeap(int[] array) {
        for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
            siftDown(array,parent,array.length);
        }
    }
 
    private static void siftDown(int[] array,int parent,int len) {
        int child = 2*parent + 1;
        while(child < len){
            if(child +1 < len && array[child] < array[child+1]){
                child++;
            }
            if(array[child] > array[parent]){
                swap(array,child,parent);
                parent = child;
                child = 2*parent + 1;
            }else {
                break;
            }
 
        }
    }
public static void swap(int[] array, int i, int j){
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

交换排序

冒泡排序

优化：

时间复杂度:0(N^2)
如果加了优化:最好情况下 可以达到0(n)

空间复杂度:0(1)

稳定性:稳定的排序
优化:每一趟都需要判断 上一趟 有没有交换

    public static void bubbleSort(int[] array){
        for (int i = 0; i < array.length-1; i++) {
            boolean flg = false;
            for (int j = 0; j < array.length -1 - i ; j++) {
                if(array[j] > array[j+1]){
                    swap(array,j,j+1);
                    flg =true;
                }
            }
            //说明上一趟没有交换，也就是有序了
            if(!flg){
                break;
            }
        }
    }
  public static void swap(int[] array, int i, int j){
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }

快速排序 

Hoare法

记录下key L和R相向出发，R找比Key小的值，L找比Key大的值，R先找找到后，L再找，两个找到交换；直到L和R相遇，相遇的位置为最后L找到的小于Key的值（让R先找的原因），此时的L就是pivot ，将Key和L交换

然后以pivot为中点，将它左右两边的循环以上操作也就是递归直到传入的L和R为相同的，那么任何一个以pivot为中点的数组都变成有序的了

pivot指的是l和r相遇的位置 

  public static void  quickSort(int[] array){
        quick(array,0, array.length-1);
    }
 
    private static void quick(int[] array,int start,int end) {
        if(start >= end){
            return;
        }
        int pivot = partitionHoare(array,start,end);
        quick(array,start,pivot-1);
        quick(array,pivot+1,end);
    }
 
    private static int partitionHoare(int[] array, int left, int right) {
        int tmp = array[left];
        int i = left;
        while(left < right){
            while(left < right && array[right] >= tmp){
                right--;
            }
            while (left < right && array[left] <= tmp){
                left++;
            }
            swap(array,left,right);
        }
        swap(array,i,left);
        return left;
    }

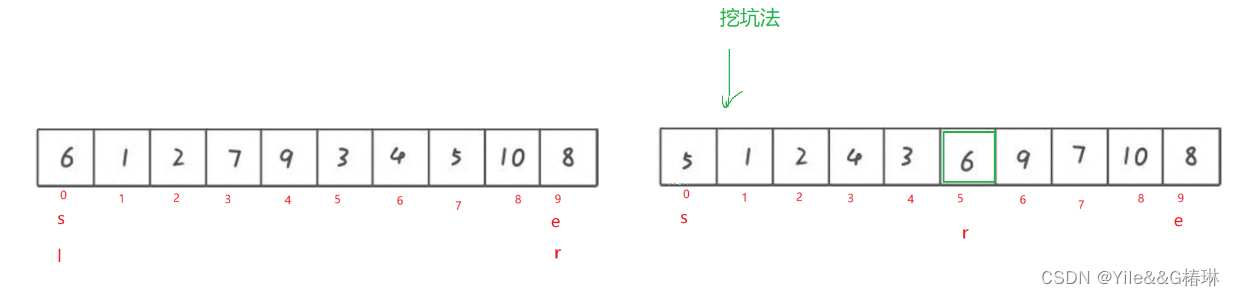
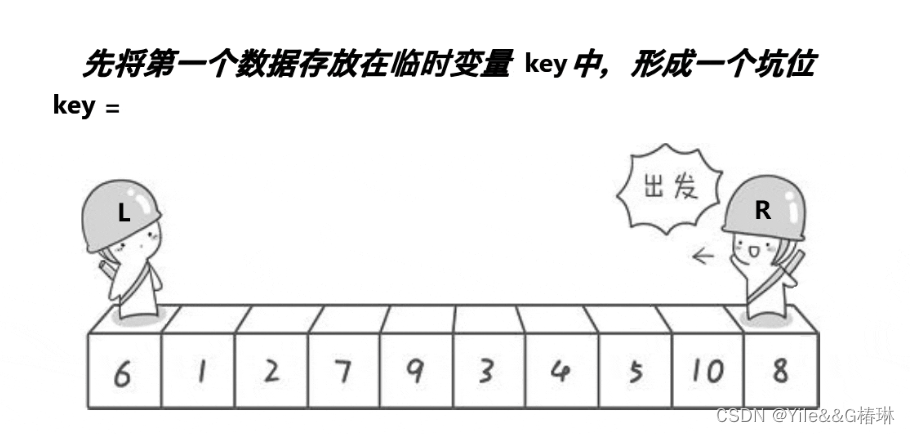
 挖坑法

向将L的第一个位置为key，也就是坑位置，然后还是R先走找到比key小的就将R下标的值给坑位，此时R为坑位，L再走，找到比L大的值，放到坑位，L此时变为坑位，直到R和L相遇，还是保证L和R相遇的时候，是R找的比Key小的放到坑位里，然后将相遇的坑位放入Key

   public static void  quickSort(int[] array){
        quick(array,0, array.length-1);
    }
 
    private static void quick(int[] array,int start,int end) {
        if(start >= end){
            return;
        }
        int pivot = partitionHole(array,start,end);
        quick(array,start,pivot-1);
        quick(array,pivot+1,end);
    }
    private static int partitionHole(int[] array, int left, int right) {
        int tmp = array[left];
        int t = left;
        while(left < right){
            while(left < right && array[right] >= tmp){
                right--;
            }
            array[left] = array[right];
            while (left < right && array[left] <= tmp){
                left++;
            }
            array[right] = array[left];
        }
        array[left] = tmp;
        return left;
    }

 

前后指针法

 

 

 记录当前电脑的时间

long startTime =System.currentTimeMillis();