我家自动化

这个屌丝很懒，什么也没留下！

热门标签

三维空间刚体运动之旋转矩阵与变换矩阵_空间旋转矩阵

作者：我家自动化 | 2024-05-07 12:35:39

踩

空间旋转矩阵

1. 旋转矩阵

1.1 点、向量和坐标系

点：点是空间中的基本元素，没有长度，没有体积；

向量：把两个点连接起来，就构成了向量，向量可以看成从某点指向另一点的一个箭头；只有当我们指定这个三维空间中的某个坐标系时，才可以谈论该向量在此坐标系下的坐标；默认向量就是列向量；
坐标系：三根不共面的轴，坐标系的三根坐标轴的方向向量就是基，坐标系能用它的基来表示；

标准正交基：两两正交、单位长度（基就是张成这个空间的一组线性无关的向量。

$eq?%5Cleft%5Be_1%2C%20e_2%2C%20e_3%5Cright%5D$

任意向量在基下的坐标（坐标 + 坐标系可以表示向量）。

$eq?%5Cboldsymbol%7Ba%7D%3D%5Cleft%5B%5Cboldsymbol%7Be%7D_1%2C%20%5Cboldsymbol%7Be%7D_2%2C%20%5Cboldsymbol%7Be%7D_3%5Cright%5D%5Cleft%5B%5Cbegin%7Barray%7D%7Bl%7D%20a_1%20%5C%5C%20a_2%20%5C%5C%20a_3%20%5Cend%7Barray%7D%5Cright%5D%3Da_1%20%5Cboldsymbol%7Be%7D_1+a_2%20%5Cboldsymbol%7Be%7D_2+a_3%20%5Cboldsymbol%7Be%7D_3$

机器人中有各种各样的坐标系

世界系 World、机体系 Body、传感器参考系 Sensor

向量点乘和叉乘

点乘（内积）：结果是一个数

$eq?%5Cboldsymbol%7Ba%7D%20%5Ccdot%20%5Cboldsymbol%7Bb%7D%3D%5Cboldsymbol%7Ba%7D%5E%7B%5Cmathrm%7BT%7D%7D%20%5Cboldsymbol%7Bb%7D%3D%5Csum_%7Bi%3D1%7D%5E3%20a_i%20b_i%3D%5Cunderset%7B%7D%7B%7C%5Cboldsymbol%7Ba%7D%7C%7C%5Cboldsymbol%7Bb%7D%7C%20%5Ccos%20%5Clangle%5Cboldsymbol%7Ba%7D%2C%20%5Cboldsymbol%7Bb%7D%5Crangle%7D$

叉乘（外积）：结果是一个向量，方向垂直于这两个向量，大小为 |a||b|sin<a,b>

$eq?%24a%20%5Ctimes%20b%3D%5Cleft%7C%5Cbegin%7Barray%7D%7Bccc%7Di%20%26%20j%20%26%20k%20%5C%5C%20a_1%20%26%20a_2%20%26%20a_3%20%5C%5C%20b_1%20%26%20b_2%20%26%20b_3%5Cend%7Barray%7D%5Cright%7C%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7Da_2%20b_3-a_3%20b_2%20%5C%5C%20a_3%20b_1-a_1%20b_3%20%5C%5C%20a_1%20b_2-a_2%20b_1%5Cend%7Barray%7D%5Cright%5D%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7D0%20%26%20-a_3%20%26%20a_2%20%5C%5C%20a_3%20%26%200%20%26%20-a_1%20%5C%5C%20-a_2%20%26%20a_1%20%26%200%5Cend%7Barray%7D%5Cright%5D%20%5Cstackrel%7B%5Ctext%20%7B%20def%20%7D%7D%7B%3D%7D%20a%5E%7B%5Cwedge%7D%20b%24$

通过上述等式，我们引入符号^，把 $eq?%24a%24$ 写成矩阵， $eq?%24a%5E%7B%5Cwedge%7D%24$ 实际上是一个反对称矩阵，可以把 $eq?%24a%20%5Ctimes%20b%24$ 写成矩阵与向量的乘法 $eq?%24a%5E%7B%5Cwedge%7D%20b%24$ ，变成线性运算。此符号是一个一一映射，意味着任意向量都对应着唯一的一个反对称矩阵，反之亦然:

$eq?a%5E%7B%5Cwedge%7D%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7D%200%20%26%20-a_3%20%26%20a_2%20%5C%5C%20a_3%20%26%200%20%26%20-a_1%20%5C%5C%20-a_2%20%26%20a_1%20%26%200%20%5Cend%7Barray%7D%5Cright%5D$

2. 坐标系间的欧式变换

2.1 欧式变换之旋转

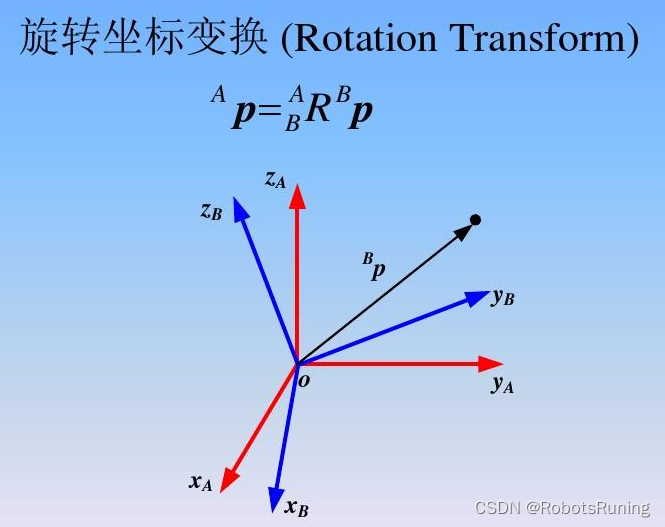
我们假设某个单位正交基 $eq?%28e_%7B1%7D%2Ce_%7B2%7D%2Ce_%7B3%7D%29$ 经过一次旋转变成了 $eq?%28e_1%27%2Ce_2%27%2Ce_3%27%29$ ，这时，对于同一个向量 $eq?%24a%24$ 它在两个基坐标系下的坐标分别为 $eq?%5Ba_1%2Ca_2%2Ca_3%5D%5ET$ 和 $eq?%5Ba_1%5E%7B%5Cprime%7D%2Ca_2%5E%7B%5Cprime%7D%2Ca_3%5E%7B%5Cprime%7D%5D%5ET$ 。因为向量本身并没有发生变化，所以下列等式成立：

$eq?%5Be_1%2Ce_2%2Ce_3%5D%5Cbegin%7Bbmatrix%7Da_1%5C%5Ca_2%5C%5Ca_3%5Cend%7Bbmatrix%7D%3D%5Be_1%27%2Ce_2%27%2Ce_3%27%5D%5Cbegin%7Bbmatrix%7Da_1%27%5C%5Ca_2%27%5C%5Ca_3%27%5Cend%7Bbmatrix%7D$

为了让两个坐标之间的关系看起来更清晰，我们将上述等式两侧同时左乘 $eq?%5Be_1%5ET%2Ce_2%5ET%2Ce_3%5ET%5D$ 此时左侧第一项将变为单位矩阵:

$eq?%24%5Cleft%5B%5Cbegin%7Barray%7D%7Bl%7Da_1%20%5C%5C%20a_2%20%5C%5C%20a_3%5Cend%7Barray%7D%5Cright%5D%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7De_1%5ET%20e_1%5E%7B%5Cprime%7D%20%26%20e_1%5ET%20e_2%5E%7B%5Cprime%7D%20%26%20e_1%5ET%20e_3%5E%7B%5Cprime%7D%20%5C%5C%20e_2%5ET%20e_1%5E%7B%5Cprime%7D%20%26%20e_2%5ET%20e_2%5E%7B%5Cprime%7D%20%26%20e_2%5ET%20e_3%5E%7B%5Cprime%7D%20%5C%5C%20e_3%5ET%20e_1%5E%7B%5Cprime%7D%20%26%20e_3%5ET%20e_2%5E%7B%5Cprime%7D%20%26%20e_3%5ET%20e_3%5E%7B%5Cprime%7D%5Cend%7Barray%7D%5Cright%5D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7Da_1%5E%7B%5Cprime%7D%20%5C%5C%20a_2%5E%7B%5Cprime%7D%20%5C%5C%20a_3%5E%7B%5Cprime%7D%5Cend%7Barray%7D%5Cright%5D%20%5Cstackrel%7B%5Ctext%20%7B%20def%20%7D%7D%7B%3D%7D%20%5Cboldsymbol%7BR%7D%20a%5E%7B%5Cprime%7D%24$

矩阵 $eq?%5Cboldsymbol%7BR%7D$ 描述了不同坐标系下同一向量的坐标变换关系。可以说，矩阵 $eq?%5Cboldsymbol%7BR%7D$ 描述了旋转本身。所以矩阵 $eq?%5Cboldsymbol%7BR%7D$ 称为旋转矩阵( Rotation Matrix)。显然，我们定义的矩阵 $eq?%5Cboldsymbol%7BR%7D$ 是由两组基之间的内积组成，实际上是各基向量夹角的余弦值，所以我们也可以称矩阵 $eq?%5Cboldsymbol%7BR%7D$ 为方向余弦矩阵 (Direction Cosine Matrix)。

同时，我们可以看出，矩阵 $eq?%5Cboldsymbol%7BR%7D$ 为正交矩阵，根据正交矩阵的性质，我们可以得到下面的关系:

$eq?a%5E%7B%5Cprime%7D%3D%5Cboldsymbol%7BR%7D%5E%7B-1%7Da%3D%5Cboldsymbol%7BR%7D%5ETa$

很明显， $eq?%5Cboldsymbol%7BR%7D%5E%7B-1%7D%28%5Cboldsymbol%7BR%7D%5ET%29$ 刻画了一个相反的旋转。

除些之外，旋转矩阵也有一些特别的性质，我们通过矩阵 $eq?%5Cboldsymbol%7BR%7D$ 的行列式可以看出，它是一个行列式为 1 的正交矩阵。反过来说，行列式为 1 的正交矩阵也是一个旋转矩阵。

根据这些性质，我们可以推广到 $eq?%24n%24$ 维旋转矩阵，可以将 $eq?%24n%24$ 维旋转矩阵的集合定义如下:

$eq?%5Cmathrm%7BSO%28n%29%3D%5C%7B%5Cboldsymbol%7BR%7D%5Cin%5Cmathbb%7BR%7D%5E%7Bn%5Ctimes%20n%7D%7C%5Cboldsymbol%7BRR%7D%5ET%3D1%2C%5Cdet%28%5Cboldsymbol%7BR%7D%29%3D1%5C%7D%7D.$

在这里， $eq?_%7BSO%28n%29%7D$ 表示的是特殊正交群(Special 0rthogonal Group)的意思，通过上式我们可以看出，这个集合由维空间的旋转拒阵组成，所以我们可以用 $eq?_%7BSO%28n%29%7D$ 表示二维空间的旋转。我们之后可以通过旋转短阵直接谈论两个坐标系之间的旋转变换，而不再通讨基表述。

2.2 两个坐标系间的欧式变换

我们经常在实际场景中定义各种各样的坐标系，如果考虑运动的机器人(即相机)，那么常见的做法是设定一个惯性坐标系(或者叫世界坐标系)，可以认为它是固定不动的。

刚体运动：两个坐标系之间的运动变换由一个旋转加上一个平移组成，这种运动就是刚体运动。相机运动就是一个刚体运动。刚体运动过程中，同一个向量在各个坐标系下的长度和夹角都不会发生变化。此时，我们说手机坐标系和世界坐标系之间，相差了一个欧氏变换(Euclidean Transform)。

旋转矩阵也有一些特别的性质，我们通过矩阵R的行列式可以看出，它是一个行列式为1的正交矩阵。反过来说，行列式为1的正交矩阵也是一个旋转矩阵

视觉SLAM十四讲 3-三维空间刚体运动_三维空间中的刚体有哪几个运动维度组成_Nismilesucc的博客-CSDN博客

视觉SLAM十四讲笔记-第三讲刚体运动_独自悠哉独自在的博客-CSDN博客

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/549265