栈和队列详解

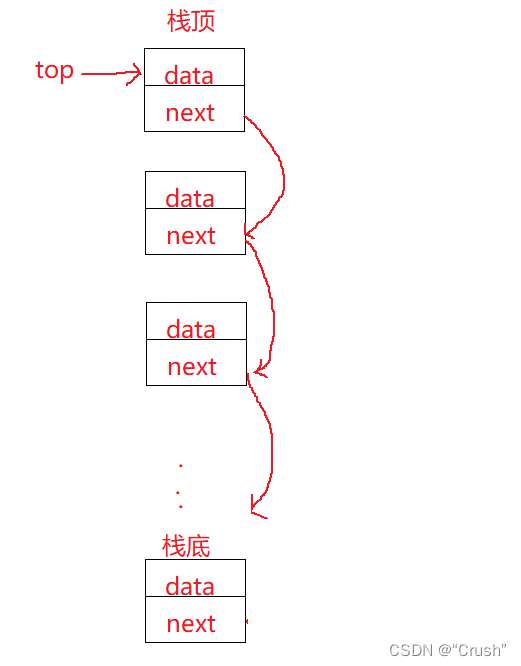
1.栈

1.1栈的概念和结构

栈：特殊的线性表，只允许在固定的一端进行插入和删除数据。
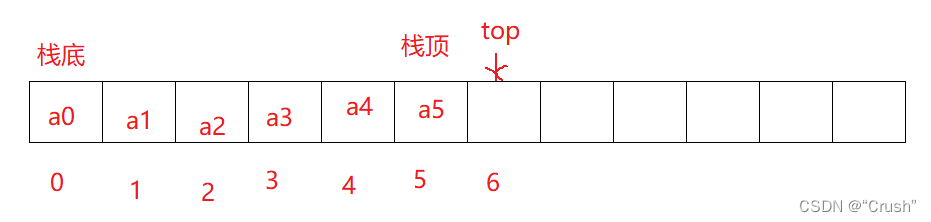
进行数据插入和删除的一端称作栈顶，另一端称作栈底。

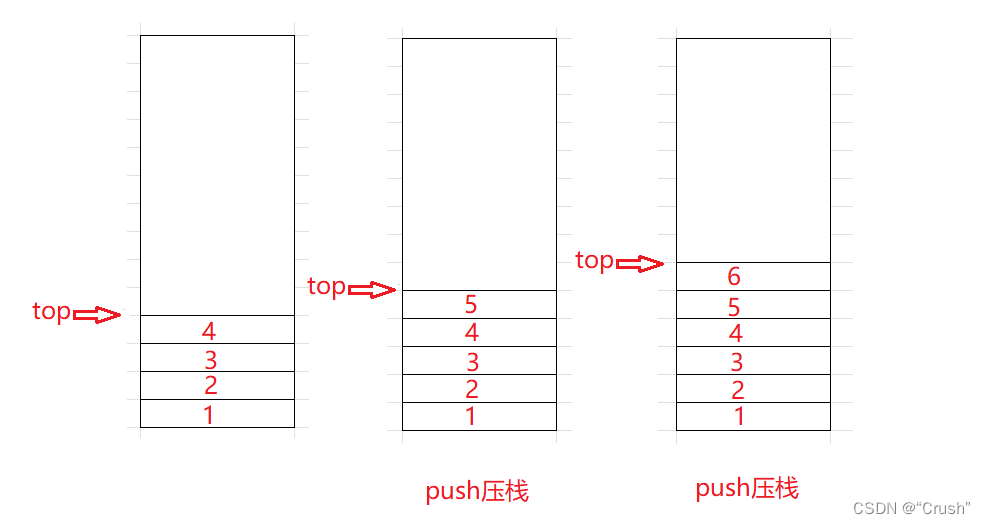
压栈：栈的插入操作称作压栈，压入栈的数据在栈顶
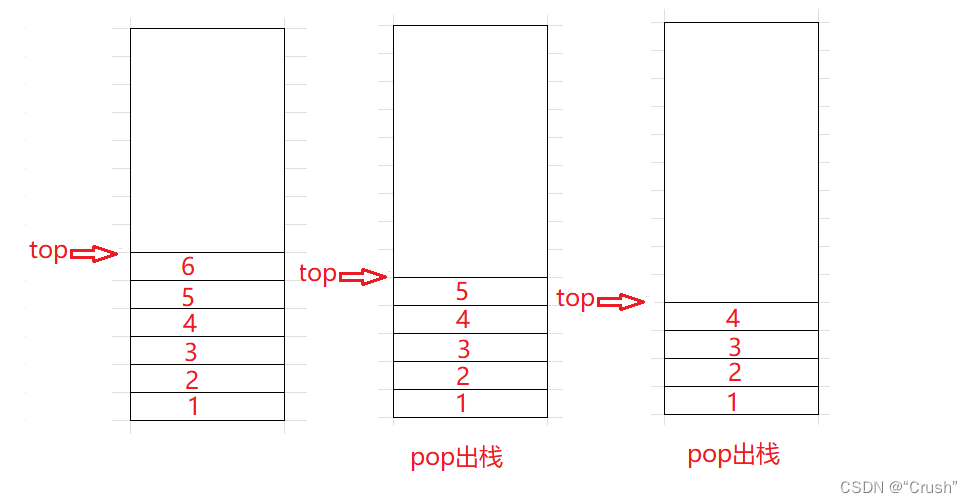
出栈：栈的删除操作称作出栈，出栈的数据也在栈顶

栈中数据遵守后进先出原则

压栈

出栈

1.2栈的实现

栈的实现有两个选择数组，链表
二者相比，数组实现栈更好些，根据栈的特点，在尾部插入数据的情况下，数组更方便。

数组实现栈

链表实现栈

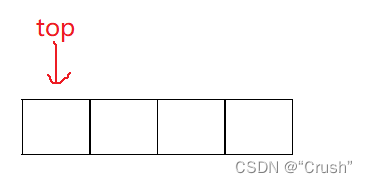
这里采取数组的结构来实现栈

定义结构体和类型

typedef int SKdatatype;

typedef struct Stack
{
	SKdatatype* a;
	int top;//记录栈中元素的个数
	int capacity;//栈的容量
}SK;
1
2
3
4
5
6
7
8

初始化栈

//初始化栈
void SKinit(SK* ps);

void SKinit(SK* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}
1
2
3
4
5
6
7
8
9

销毁栈

//销毁栈
void SKdestory(SK* ps);

void SKdestory(SK* ps)
{
	assert(ps);
	ps->capacity = ps->top = 0;
	free(ps->a);
	ps->a = NULL;
}
1
2
3
4
5
6
7
8
9
10

数据压栈

//压栈
void SKpush(SK* ps, SKdatatype x);

void SKpush(SK* ps, SKdatatype x)
{
	assert(ps);

	//检查容量
	if (ps->capacity == ps->top)
	{
		int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SK* tmp = (SK*)realloc(ps->a, newcapacity * sizeof(SK));
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = newcapacity;
		ps->a = tmp;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

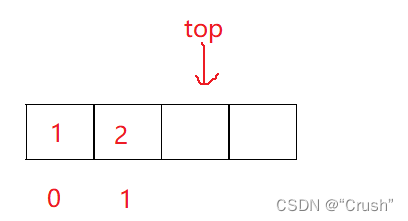
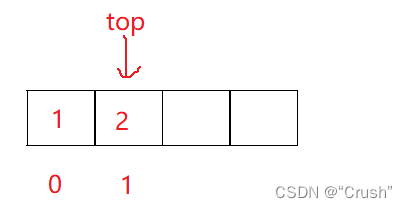
压入两个数据进栈，监视如下

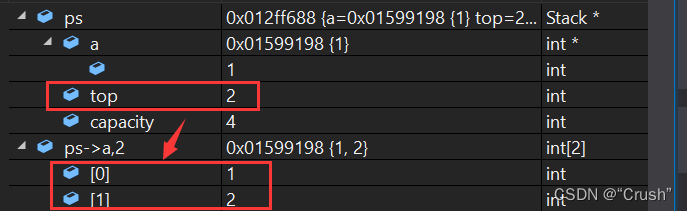
栈顶ps->top此时是2,说明栈中已经有两个数据。

数据出栈

//出栈
void SKpop(SK* ps);

void SKpop(SK* ps)
{
	assert(ps);
	assert(!SKempty(ps));
	ps->top--;
}
1
2
3
4
5
6
7
8
9

数组中删除元素，不需要清除元素

将栈顶的数据出栈，监视如下

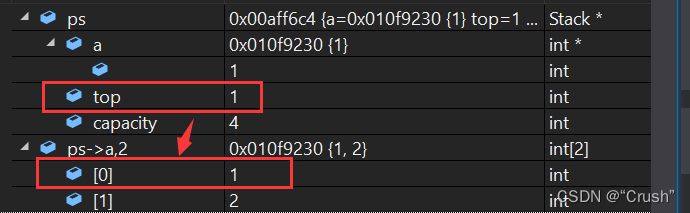
栈顶ps->top此时是1,从上面可知，栈顶的数据已经出栈，栈中还有一个数据。

获得栈顶元素

//获得栈顶元素
SKdatatype SKtop(SK* ps);

SKdatatype SKtop(SK* ps)
{
	assert(ps);
	assert(!SKempty(ps));

	return ps->a[ps->top - 1];
}
1
2
3
4
5
6
7
8
9
10

检查栈是否为空

//检查是否是空栈
bool SKempty(SK* ps);

bool SKempty(SK* ps)
{
	assert(ps);

	return ps->top == 0;
}
1
2
3
4
5
6
7
8
9

计算栈中的数据个数

//计算栈中数据的个数
int SKsize(SK* ps);

int SKsize(SK* ps)
{
	assert(ps);
	return ps->top;
}
1
2
3
4
5
6
7
8

2.队列

2.1队列的概念及结构

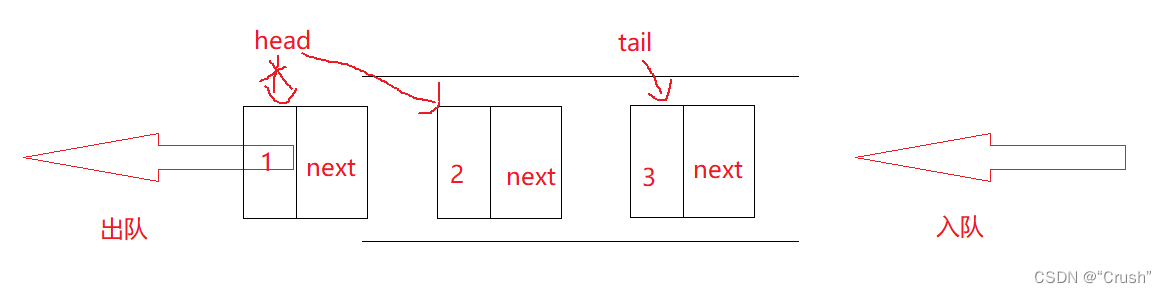
队列：只允许在一端进行插入数据操作，另一端进行删除数据操作的特殊线性表
队列遵守先进先出原则
队尾：进行插入数据操作的一端
队头：进行删除数据操作的一端

2.2队列的实现

队列的实现也同样有两种选择：数组，链表。二者相比之下，链表更好些，因为链表的特点头删的效率很高。

数据入队，尾部插入

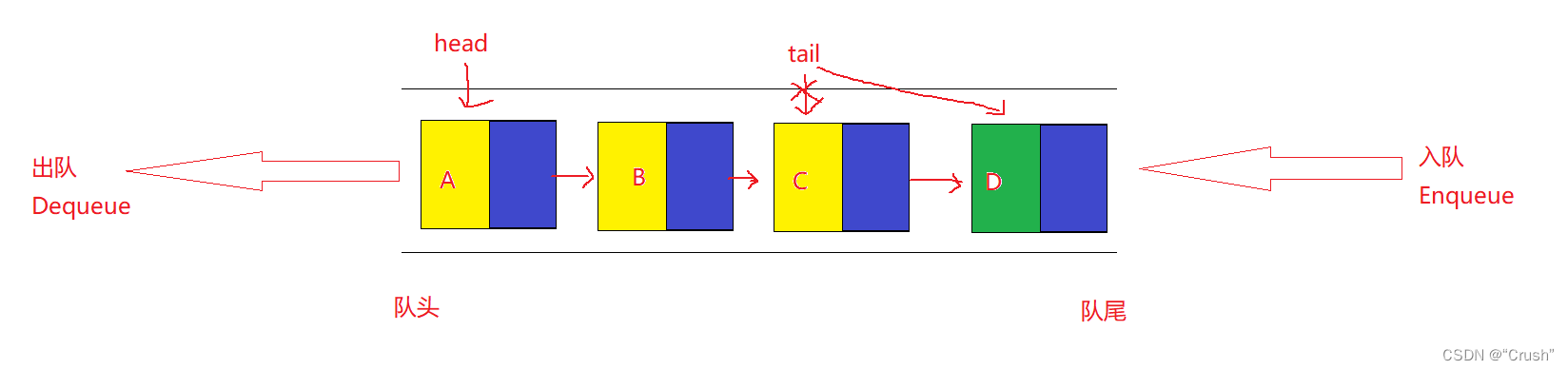
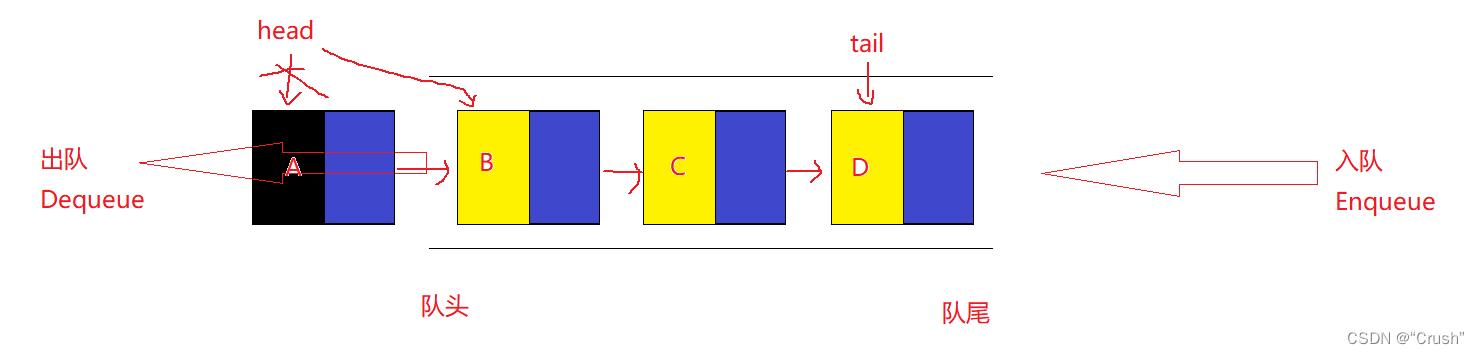
数据出队，头部删除

定义结构体和类型

为了方便数据的增删查改，这里定义队列的头尾指针

typedef int Queuedatatype;
typedef struct Queuenode
{
	struct Queuenode* next;
	Queuedatatype data;
}QEnode;


typedef struct Queue
{
	QEnode* head;//队首指针
	QEnode* tail;//队尾指针
	int size;//用于记录队列中数据个数
}QE;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

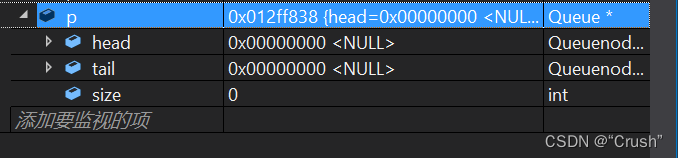
队列的初始化

//初始化队列
void QEinit(QE* p);

void QEinit(QE* p)
{
	assert(p);
	p->size = 0;
	p->head = p->tail = NULL;
}

1
2
3
4
5
6
7
8
9
10

队列的销毁

//销毁队列
void QEdestory(QE* p);

void QEdestory(QE* p)
{
	assert(p);

	QEnode* cur = p->head;
	while (cur)
	{
		QEnode* del = cur;
		cur = cur->next;
		free(del);
	}
	p->head = p->tail = NULL;
	p->size = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

数据从队尾插入队列

//数据插入队列
void QEpush(QE* p,Queuedatatype x);

void QEpush(QE* p,Queuedatatype x)
{
	assert(p);
	QEnode* newnode = (QEnode*)malloc(sizeof(QEnode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->next = NULL;
	}


	if (p->tail == NULL)
	{
		p->head = p->tail = newnode;
	}
	else
	{
		p->tail->next = newnode;
		p->tail = p->tail->next;
	}

	p->size++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

将三个数据从队尾插入队列中，监视如下，此时size==3,表示队列中已经插入三个数据

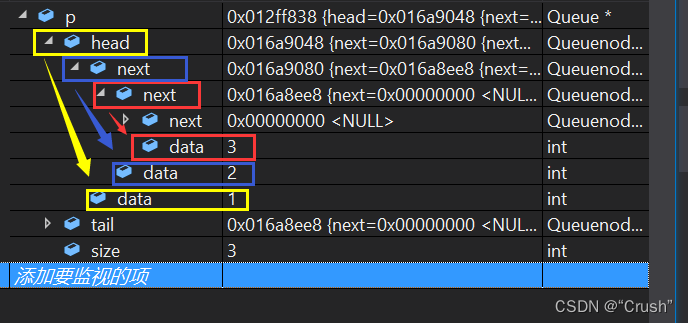
读取队首数据

//读取队首数据
Queuedatatype QEfront(QE* p);

Queuedatatype QEfront(QE* p)
{
	assert(p);
	assert(!QEempty(p));
	return p->head->data;
}
1
2
3
4
5
6
7
8
9

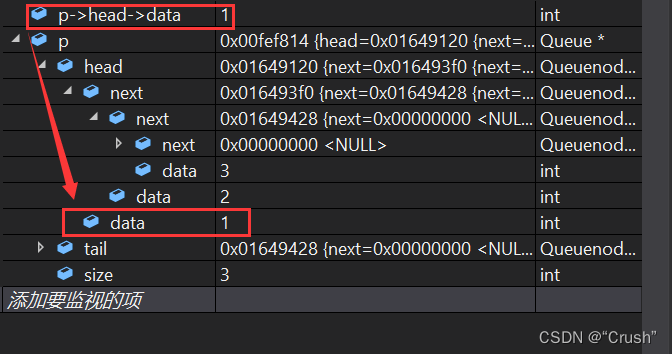
读取队尾数据

//读取队尾数据
Queuedatatype QEback(QE* p);

Queuedatatype QEback(QE* p)
{
	assert(p);
	assert(!QEempty(p));
	return p->tail->data;
}
1
2
3
4
5
6
7
8
9

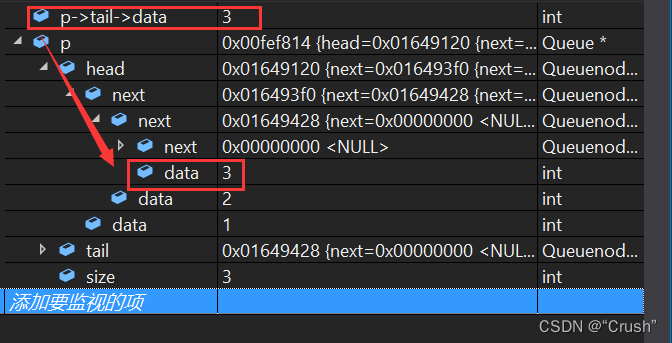
检查队列是否为空

//检查队列是否为空
bool QEempty(QE* p);

bool QEempty(QE* p)
{
	assert(p);

	return p->head == NULL && p->tail == NULL;
}
1
2
3
4
5
6
7
8
9

数据从队首删除

//数据出队列
void QEpop(QE* p);

void QEpop(QE* p)
{
	assert(p);
	assert(!QEempty(p));
	if (p->head->next == NULL)
	{
		free(p->head);
		p->head = p->tail = NULL;
	}
	else
	{
		QEnode* del = p->head;
		p->head = p->head->next;
		free(del);
		del = NULL;
	}
	p->size--;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

将一个数据从队首删去，此时队列中只剩余两个个数据，监视如下

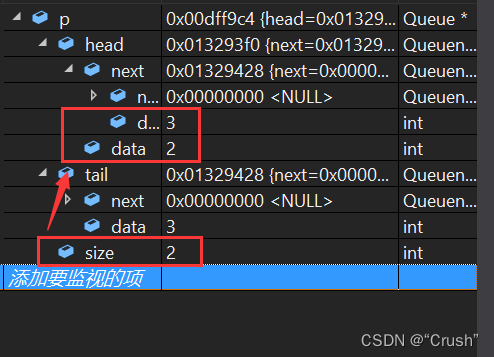
计算队列中数据的个数

//计算队列中数据的个数
int QEsize(QE* p);

int QEsize(QE* p)
{
	assert(p);

	return p->size;
}
1
2
3
4
5
6
7
8
9

2.3扩展

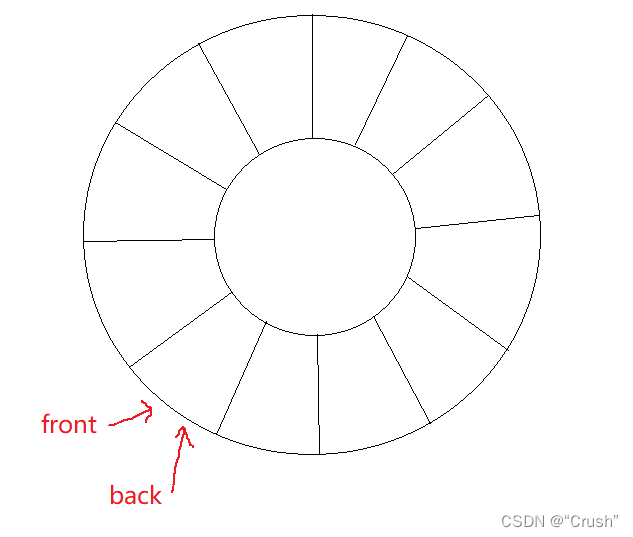
特殊的一种队列：循环队列
同样的道理循环队列的实现也有两种方式：数组，链表

空的环形队列

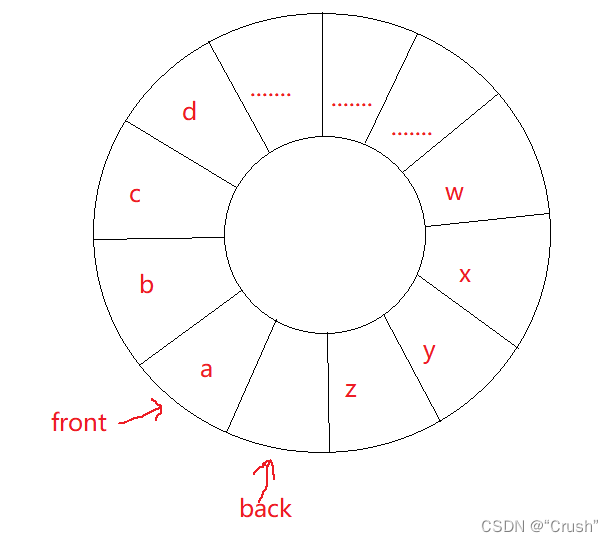
满的环形队列

既然说到环形队列，不如思考思考如何去实现？

首先实现方式有两种：数组，队列。

由于在读取队尾数据时，如果遇到如下情况，则不能进行读取数据
还需要定义一个位于 back 前一个位置的指针，比较麻烦。

所以采用数组实现环形队列

注意
采用数组实现环形队列，存在一个问题：队列空和队列满无法区分。
解放方法有两个：

1. 创建结构体时，额外加一个用于记录数据个数的变量
2. 额外增加一个空间，队列满时永远留一个空位置

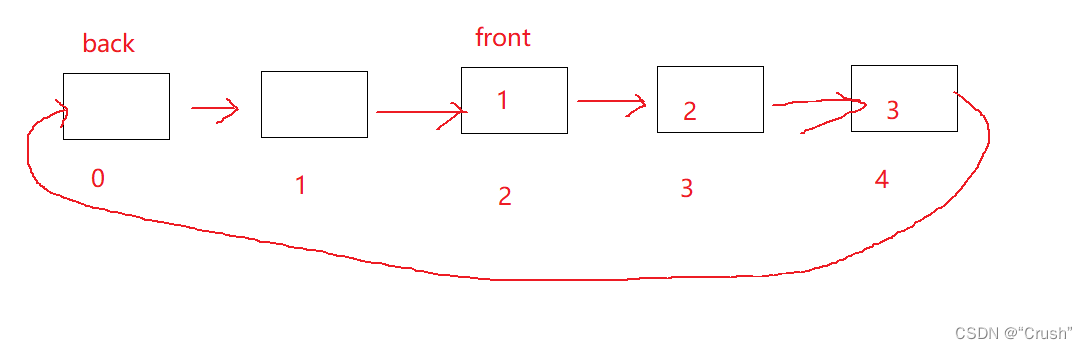
定义结构体

typedef struct 
{
    int*a;//数组，用于存储数据
    int front;//队头指针
    int back;//队尾指针
    int n;//环形队列中数据的总数
} MyCircularQueue;
1
2
3
4
5
6
7

初始化环形队列

MyCircularQueue* myCircularQueueCreate(int k) 
{
    //环形队列开辟空间
    MyCircularQueue*obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    //数组开辟空间
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->back=0;
    //环形队列的长度
    obj->n=k+1;
    return obj;
}
1
2
3
4
5
6
7
8
9
10
11

环形队列初始化

MyCircularQueue* myCircularQueueCreate(int k) 
{
    MyCircularQueue*obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->back=0;
    obj->n=k+1;
    return obj;
}
1
2
3
4
5
6
7
8

front指向队头
back指向队尾的下一个位置

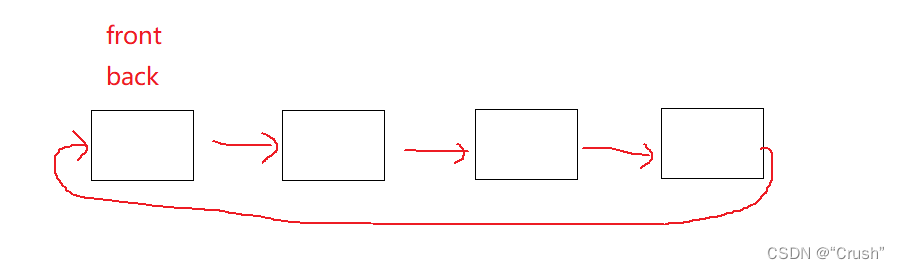
检查环形队列是否为空

bool myCircularQueueIsEmpty(MyCircularQueue* obj) 
{
    return obj->front==obj->back;
}
1
2
3
4

检查环形队列是否已满

bool myCircularQueueIsFull(MyCircularQueue* obj) 
{
    return (obj->back+1)%obj->n==obj->front;
}
1
2
3
4

数据入队

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) 
{
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }

    obj->a[obj->back]=value;
    obj->back++;
    
    //防止back指针指向数组的最后
    //再次++，导致数组越界
    obj->back%=obj->n;

    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

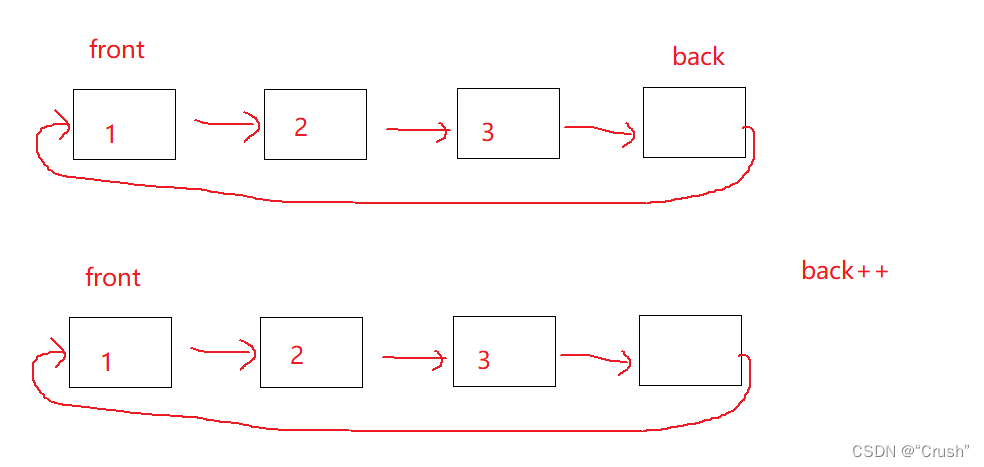
数据出队

bool myCircularQueueDeQueue(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    obj->front++;
    obj->front%=obj->n;
    return true;
}
1
2
3
4
5
6
7
8
9
10

读取队头

int myCircularQueueFront(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {
        return obj->a[obj->front];
    }
}
1
2
3
4
5
6
7
8
9
10
11

读取队尾

int myCircularQueueRear(MyCircularQueue* obj) 
{
    if(myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    else
    {   //避免back指针指向队头，向前一个位置访问读取数据时
        //导致数组越界
        return obj->a[(obj->back-1+obj->n)%(obj->n)];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

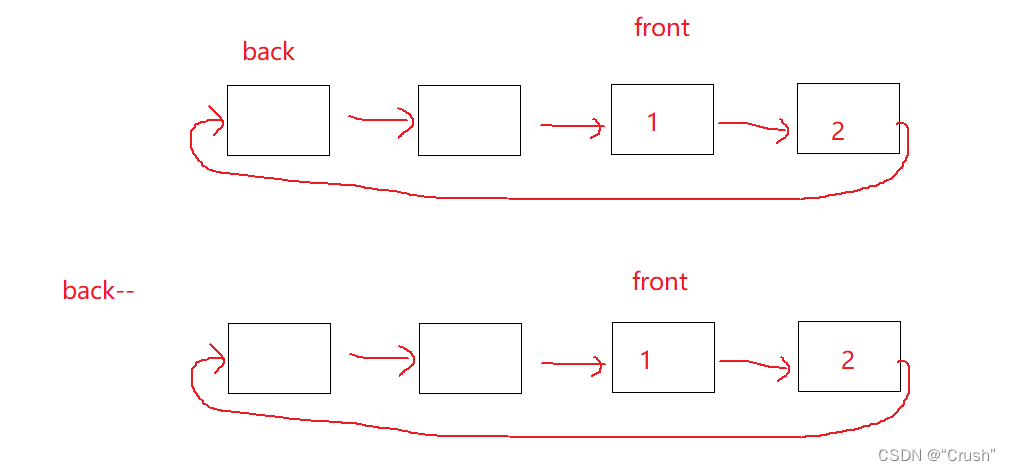
销毁环形队列

void myCircularQueueFree(MyCircularQueue* obj) 
{
    free(obj->a);
    free(obj);
}
1
2
3
4
5

3.队列实现栈

使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）

首先思考队列的栈对于数据进出所遵循的原则，队列是先进先出而栈是先进后出。
既然这两种线性表所遵循的原则不相同，又该用什么方式去实现呢？

两个队列是关键点，接下来就思考两个队列如何去实现队列。

假设只有一个队列中有数据，另一个队列为空。

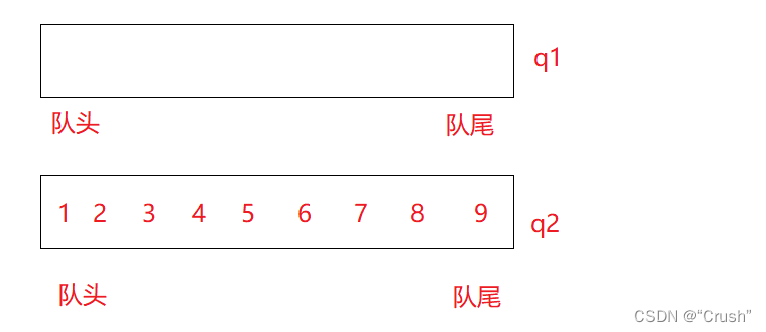
此时队列 q2 删除数据的话，只能从队头删除，这样就不符合栈先进后出的原则。

如果将队列 q2 只留下队尾的数据，其余的全部转移到队列 q1 中，这时删除 q2 中数据就符合后进先出的原则。

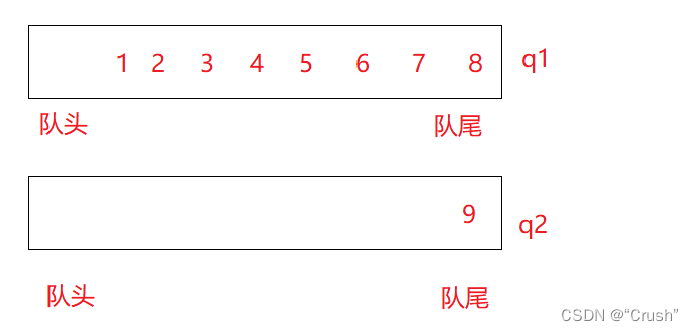
同样的道理如果再次删除数据，就将队列 q1 中除队尾以外的数据转移到队列 q2 中，再进行删除操作。

由此便得到思路：保持一个队列为空，删除数据时，将另一个不为空的队列的数据除队尾以外全部转移到空队列中。

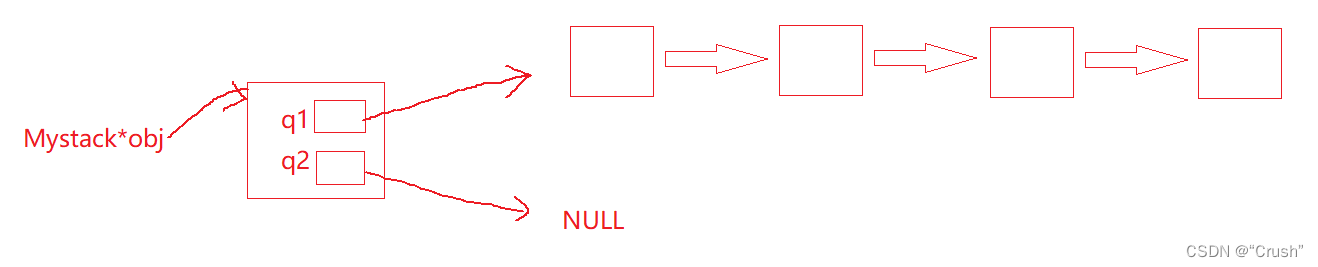
定义两个队列

typedef struct {
    QE q1;
    QE q2;
} MyStack;
1
2
3
4

两个队列实现栈，并进行初始化

MyStack* myStackCreate()
{
    MyStack*obj=(MyStack*)malloc(sizeof(MyStack));
    QEinit(&obj->q1);
    QEinit(&obj->q2);
    return obj;
}
1
2
3
4
5
6
7

数据入栈

void myStackPush(MyStack* obj, int x) 
{
    if(!(QEempty(&obj->q1)))
    {
        QEpush(&obj->q1,x);
    }
    else
    {
        QEpush(&obj->q2,x);
    }
}
1
2
3
4
5
6
7
8
9
10
11

这里假设队列 q2 不为空

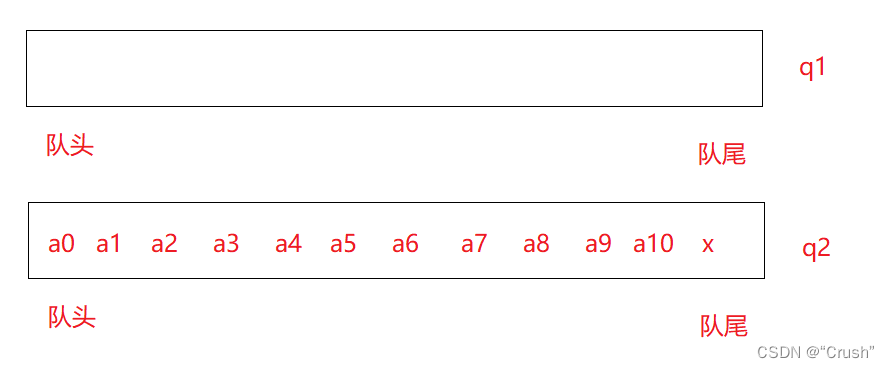
数据出栈

先判断队列 q1,q2 哪个为空，哪个不为空

假设队列 q2 不为空，将其 N-1 个数据转移到 队列 q1 中，接着将最后一个数据出栈

int myStackPop(MyStack* obj) 
{
    QE*empty=&obj->q1;
    QE*nonempty=&obj->q2;
    if(!QEempty(&obj->q1))
    {
        empty=&obj->q2;
        nonempty=&obj->q1;
    }
    //将队列中的N-1个数据，转移到空队列中
    while(QEsize(nonempty)>1)
    {
        QEpush(empty,QEfront(nonempty));
        QEpop(nonempty);
    }
    //取出栈顶数据（也就是不为空队列的最后一个数据）
    int top = QEfront(nonempty);
    //删除不为空队列最后一个数据
    QEpop(nonempty);
    //返回栈顶数据
    return top;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

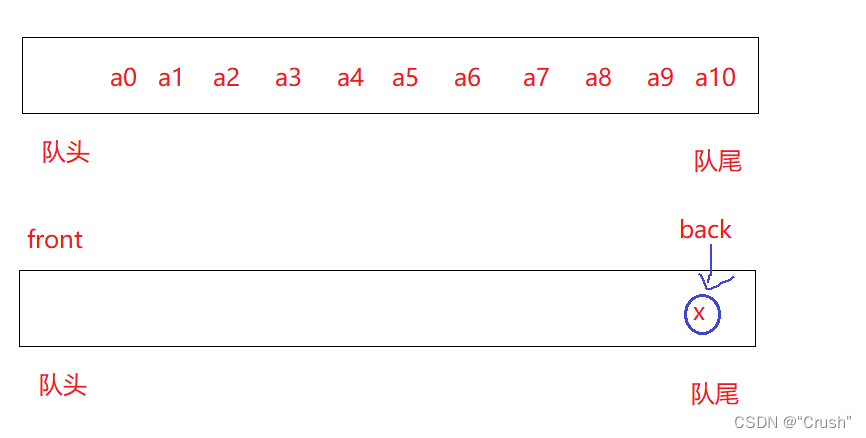
读取栈顶数据

先判断哪个队列不为空，读取不为空队列的队尾数据，即栈顶数据

int myStackTop(MyStack* obj) {
    if(!QEempty(&obj->q1))
    {
        return QEback(&obj->q1);
    }
    else
    {
        return QEback(&obj->q2);
    }
}
1
2
3
4
5
6
7
8
9
10

判断栈是否为空

必须队列 q1 ,q2 都为空，才能说明栈也为空

bool myStackEmpty(MyStack* obj) {
    assert(obj);
    return QEempty(&obj->q1)&&QEempty(&obj->q2);
}
1
2
3
4

销毁栈

销毁栈，不可以直接释放栈开辟的空间，会造成内存泄漏

因为队列q1 q2 中也有开辟的空间，直接释放栈开辟的空间，会导致再也找不到队列开辟的空间，从而造成内存泄漏

所有先将队列销毁，最后再释放栈开辟的空间

void myStackFree(MyStack* obj) {
    QEdestory(&obj->q1);
    QEdestory(&obj->q2);
    free(obj);
}
1
2
3
4
5

4.栈实现队列

既然队列可以实现栈，那么栈是否可以实现队列呢？

答案是：当然可以

与上面类似，都是需要两个，也就是通过两个队列去实现栈

由于栈所遵守的原则是先进后出，所以不需要将其中一个栈一直保存空的状态

接下来开始慢慢分析

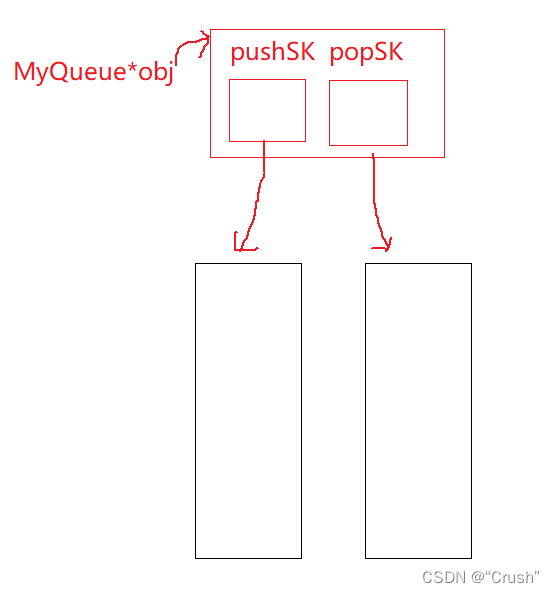
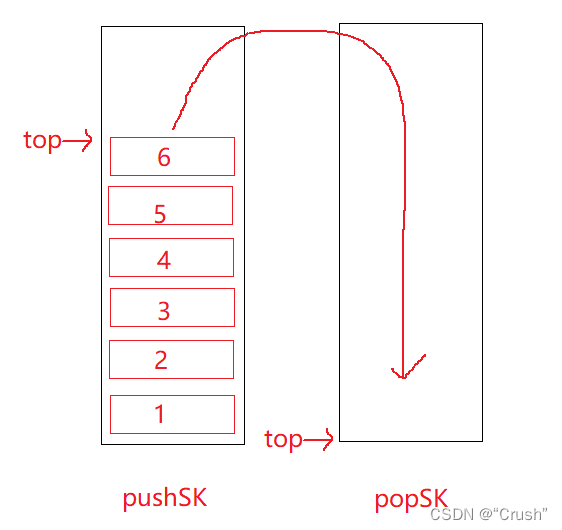
两个栈 其中 pushSK 是插入数据的栈，popSK 是删除数据的栈

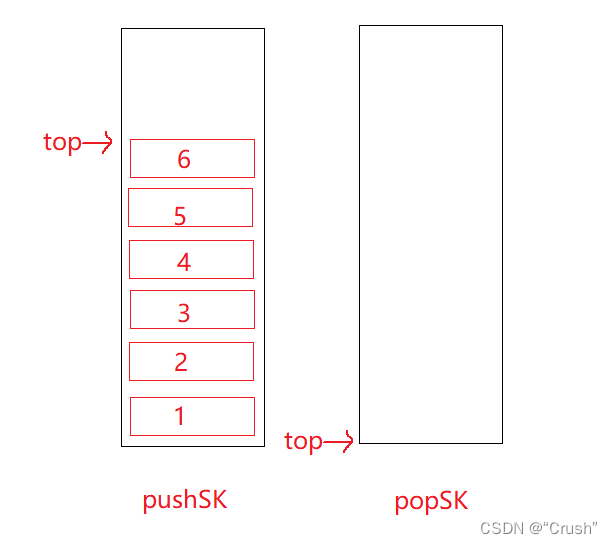
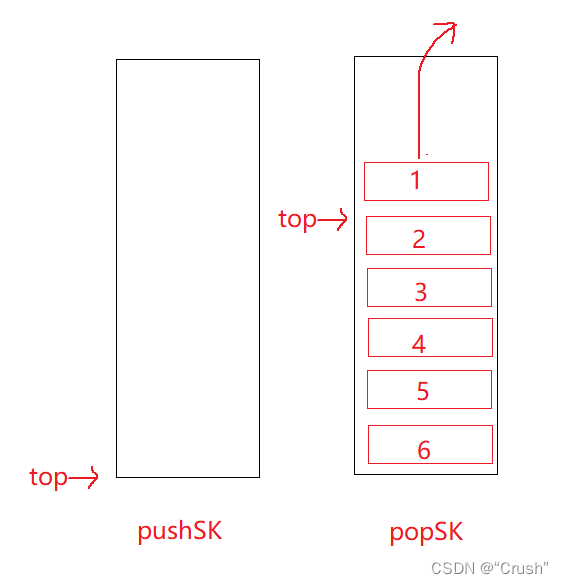
如果此时删除数据，按照队列的原则需要将第一个插入的数据进行删除操作，也就是删除位于栈底的 1 。很简单只需要将 pushSK 中的所有数据全部转移到 popSK 中即可。然后在 popSK 中删除栈顶数据 1，就完成队列的数据删除

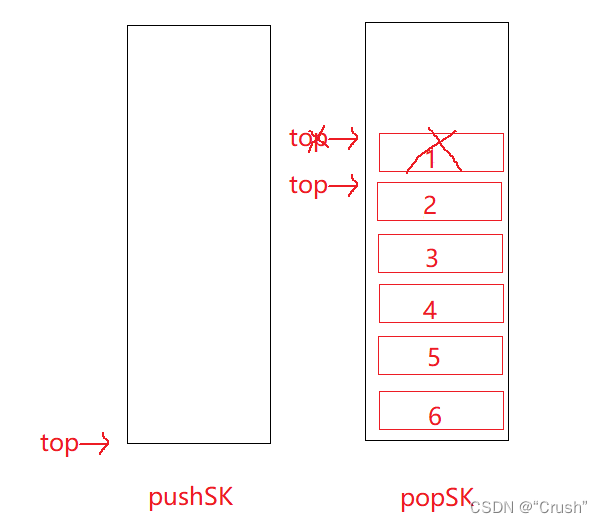
如果继续删除数据，便可直接在 popSK 中删除，直到栈 popSK 为空，再将栈 pushSK 中的数据全部转移到其中。

由此可得出思考：
插入数据到pushSK 中，然后将pushSK 中的数剧全部转移到 popSK 中，当 popSK为空，再重复此操作。
由于栈的特点，转移的数据再 popSK 中全部都是倒置的，因此符合队列的特点。

定义两个栈 pushSK,popSK

typedef struct 
{
    SK pushSK;//数据压入栈
    SK popSK;//数据压出栈
} MyQueue;
1
2
3
4
5

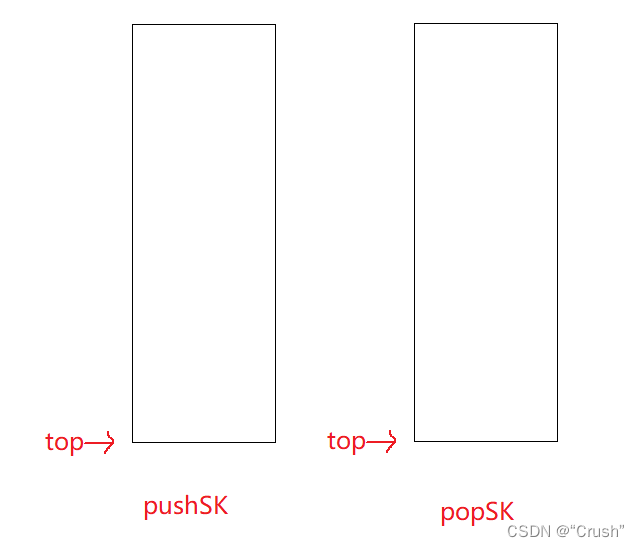
初始化两个栈

MyQueue* myQueueCreate() 
{
    MyQueue*obj=(MyQueue*)malloc(sizeof(MyQueue));
    SKinit(&obj->pushSK);
    SKinit(&obj->popSK);

    return obj;
}
1
2
3
4
5
6
7
8

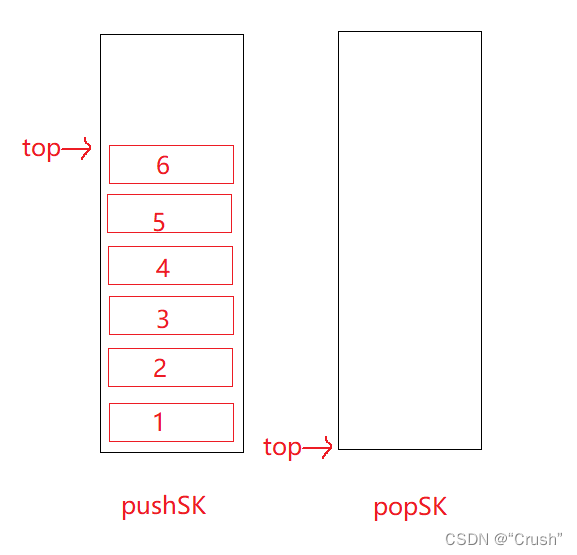
数据插入队列

void myQueuePush(MyQueue* obj, int x) 
{
    SKpush(&obj->pushSK,x);
}
1
2
3
4

数据出队列

在删除队头的数据时，需要判断 栈 popSK 是否为空。如果为空，则不能完成删除操作。

为了方便起见，将判断这一过程独立为函数，在之后还能用到

void pushSKtopopSK(MyQueue*obj)
{
    if(SKempty(&obj->popSK))
    {
        while(!SKempty(&obj->pushSK))
        {
            SKpush(&obj->popSK,SKtop(&obj->pushSK));
            SKpop(&obj->pushSK);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11

int myQueuePop(MyQueue* obj) 
{
    if(SKempty(&obj->popSK))
    {
        pushSKtopopSK(obj);
    }

    int top=SKtop(&obj->popSK);
    SKpop(&obj->popSK);

    return top;
}
1
2
3
4
5
6
7
8
9
10
11
12

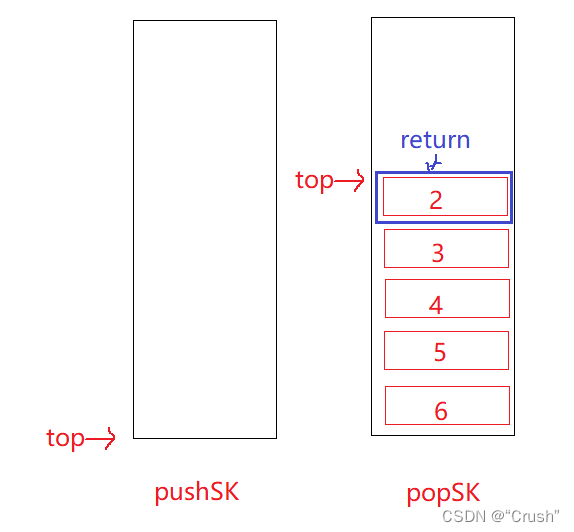
读取队头数据

int myQueuePeek(MyQueue* obj) 
{
    if(SKempty(&obj->popSK))
    {
        pushSKtopopSK(obj);
    }
    return SKtop(&obj->popSK);
}
1
2
3
4
5
6
7
8

判断队列是否为空

栈 pushSK和 栈 popSK 必须都为空，队列才表示为空

bool myQueueEmpty(MyQueue* obj) 
{
    return SKempty(&obj->pushSK)&&SKempty(&obj->popSK);
}
1
2
3
4

销毁队列

与上面类似，不能直接释放队列所开辟的空间，否则同样会造成内存泄漏

void myQueueFree(MyQueue* obj) 
{
    SKdestory(&obj->pushSK);
    SKdestory(&obj->popSK);
    free(obj);
}
1
2
3
4
5
6