长尾学习（一）：Long-Tail Learning via Logit Adjustment

一、背景

    这是一篇从损失函数入手解决长尾问题的一种新思路，借鉴基于标签频次的logit adjustment方法，鼓励模型在高频类别与低频类别之间的Margin较大，提出了两种校准方法：

• 事后校准（post-hoc adjustment）
• 事中校准（修改损失函数）

    理论证明该方法保证了Fisher consistent（损失函数降到最小时，识别错误率也会最小），同时实验证明该方法的效果也是非常不错的。这也是本人比较欣赏该方法的主要原因之一，其次是该方法简单易用，可以轻而易举的切入分类、检测等任务当中去。总感觉事后校准比较奇怪，具体所以然但是也说不出来，所以重点篇幅放在事中校准的介绍。

二、已有方法的局限

    作者通过分析已有的一些类似方法，指出了它们存在的局限：

1.  基于权重正则的方法严重依赖所使用的优化器
2.  基于修改损失的方法不满足Fisher consistent

三、The logit adjusted loss

    在事中模式下，基于贝叶斯最优的统计推理证明（这个参考原文第3节，比较晦涩），提出了一种交叉熵的变种，如下：

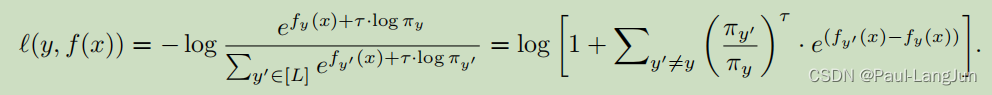
    简单来说，就是在每个logit上加入一个偏移量（ 可以用归一化到0-1之间的类别样本占比来表示，比如0.99,0.01等等），同时给出了该函数的一般形式，如下：

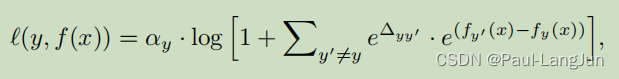
    这个形式涵盖了普通的交叉熵和变种交叉熵，而且是已有的一些其他类似方法的一般形式，具体可以参见原文。按照原文的解释，它可以灵活的控制不同类别对损失函数的贡献。