SPSS常用的几种统计分析_spss统计分析

数据已经放在评论区了

实验1：地理数据的统计处理

实验步骤与结果分析：

1.点击菜单栏【文件】下拉选项框，打开已经下载好的Excel表“"D:\桌面\计量地理学实习\表2-1某地区有关农业统计数据.xls"”，如下图所示：

2.点击菜单栏上面的【分析】—【描述统计】—【频率】工具，如下图所示：

​3.将需要进行统计分析的变量选中加载到右边，点击确定得到如下结果（每个变量因子的频数统计表）：

4.选中【分析】—【描述统计】—【描述】工具，将需要进行统计分析的变量选中加载到右边，如下图所示：

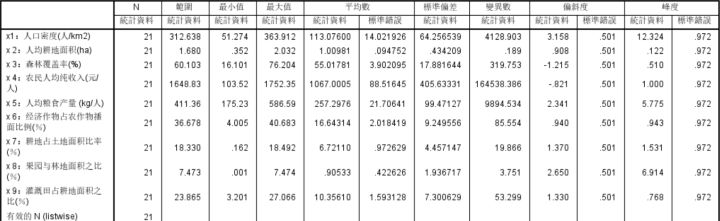
5.点击确定得到如下输出结果（每个变量的统计参数）：

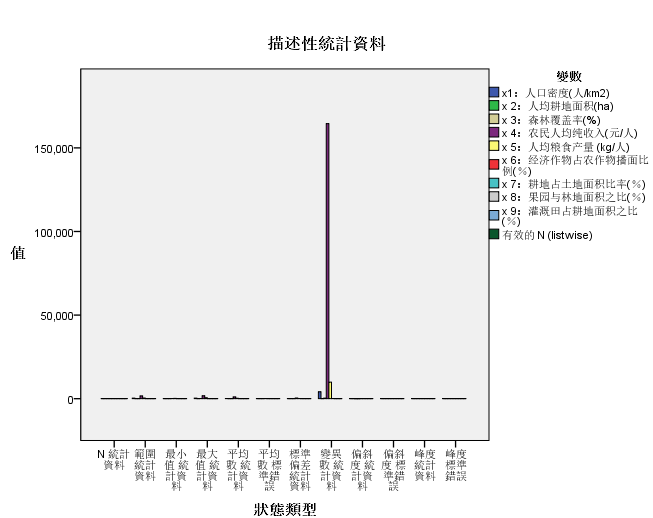
​6.最后将其导出为柱状图，更加直观的查看各个变量之间的统计参数差别，导出图表如下图所示：

​

实验2：相关分析

实验步骤与结果分析

1.实验数据整理准备后加载到SPSS，如下图所示：

1. 在进行双变量相关分析前，我们需要对数据进行相关性检验，选中菜单栏【图形】|【回归变量图】

1. 将两个变量分别加载进来，如下图所示：

可以看到两者之间是属于负相关。

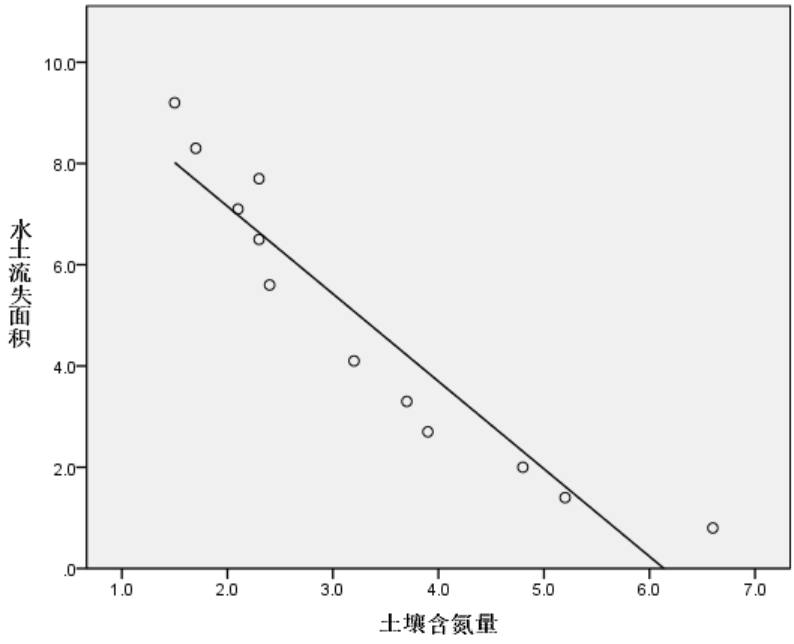
4.由于我们的相关分析是两个变量之间的分析，为此我们打开【分析】—【相关】—【双变量】工具，将两个变量【水土流失面积】和【土壤含氮量】加载进去，

5.从表中可以看到，水土流失面积和土壤含氮量存在相关关系，其相关系数为-0.946，呈现中度相关性，且在0.01的显著性水平上显著，即样本数据中的这个相关性在总体中一样有效。

实验3：主成分分析

实验步骤与结果分析：

1.数据准备，在SPSS载入“"D:\桌面\计量地理学实习\主成分分析.xlsx"”数据，如下图所示：

2.打开【分析】|【降维】|【因子分析】工具，将数据中除了【城市】这个变量，其余变量全部添加进去，

3.点击【描述】，勾选新打开界面的【系数】选项和【抽取】中的【碎石图】选项（使得分析结果更为直观），如下图所示：

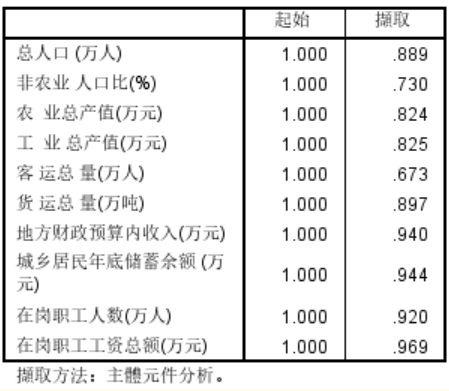
1. 点击确定得到主成分分析运算结果。在公因子方差（Communalities）表中，给出了因子载荷阵的初始公因子方差（Initial）和提取公因子方差（Extraction）。

​总方差解释：

​

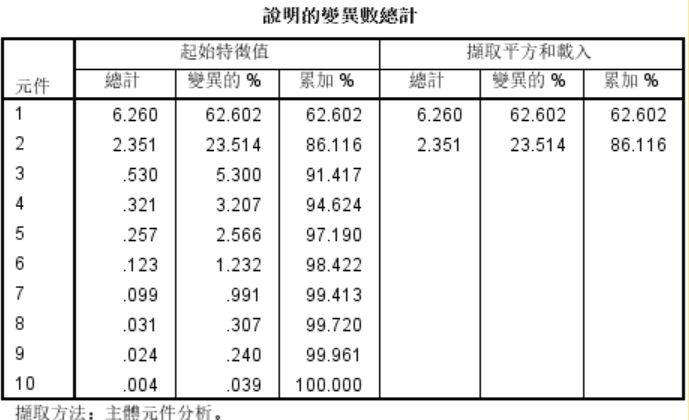
5.该表按顺序排列出主成分得分的方差（Total），在数值上=相关系数矩阵的各个特征根λ，因此可以直接根据特征根计算每一个主成分的方差百分比和方差累计值。由图可知，主成分是两个，都是方差（特征根）大于1的，第一主成分占比重62.602%，第二主成分占比重23.514%，这两个主成分达到85.116%，超过了85%，可以说用这两个指标评价各省份的经济可以近似代替原来的10个指标。主成分的数目可以根据相关系数矩阵的特征根来判定。相关系数矩阵的特征根刚好等于主成分的方差，而方差是变量数据蕴涵信息的重要判据之一。

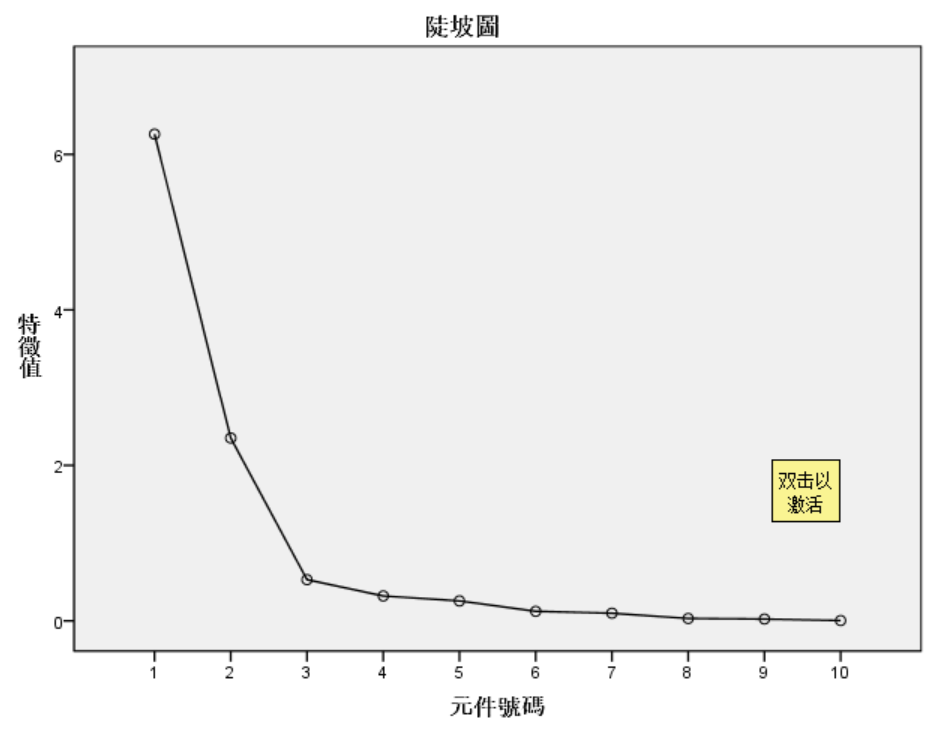
​6.从碎石图看的话也可以知道由图直观的看出，成分1、2包含了大部分信息，从3开始就基本趋向平稳状态了。

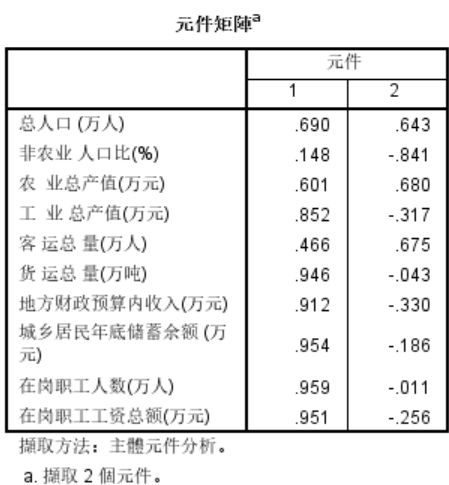
7.该表是主成分载荷矩阵，每一列载荷值都显示了各个变量与有关主成分的相关系数。以第一列为例，0.69实际上是总人口与第一个主成分的相关系数。

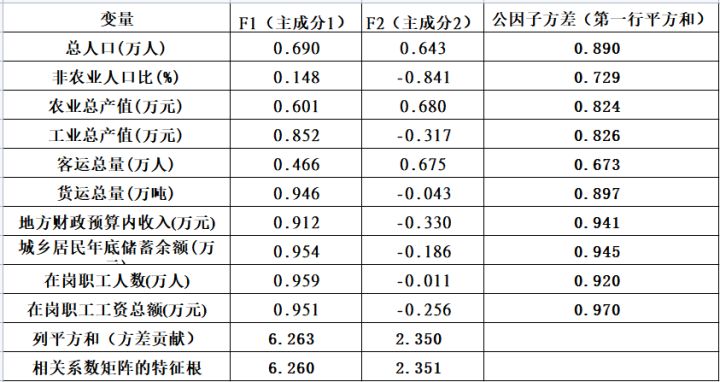
8.事实上，有如下关系成立：相关系数矩阵的特征根＝方差贡献＝主成分得分的方差。两个主成分可以解释各个变量达到了最小72.9%，最大97%，如果我们将8个主成分全部提取，则主成分载荷的行平方和都等1，就是第一张表上面的起始公因子方差。到此可以明白：在Communalities中，Initial对应的是初始公因子方差，实际上是全部主成分的公因子方差，Extraction对应的是提取的主成分的公因子方差，我们提取了两个主成分，故计算公因子方差时只考虑两个主成分。

提取主成分的原则上要求公因子方差的各个数值尽可能接近，亦即要求它们的方差小，当公因子方差完全相等时，它们的方差为0，这就达到理想状态。实际应用中，只要公因子方差数值彼此不相差太远就行了。从上面给出的结果可以看出：提取两个主成分的时候，变量客运总量（万人）的公因子方差偏小，这暗示提取2个主成分，客运总量（万人）方面的信息可能有较多的损失。至于方差贡献，反映对应主成分的重要程度。

总结，决定主成分数目的3个原则：1.只取λ>1的特征根对应的主成分；2.累计百分比达到80%~85%以上的λ值对应的主成分；3.根据特征根变化的突变点决定主成分的数量；

9.接下来根据得到的特征值和主成分载荷值（需要复制到excel表中整理在SPSS打开）计算每一个变量的特征向量，打开【转换】|【计算变量】工具，在目标变量中输入新的名字，输入公式：V1（第一主成分的载荷值）/SQRT（第一主成分的特征值6.26），对于第二主成分计算其特征向量也是一样的操作。

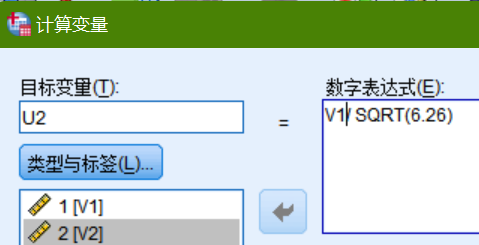
10.两个主成分的特征向量计算结果：

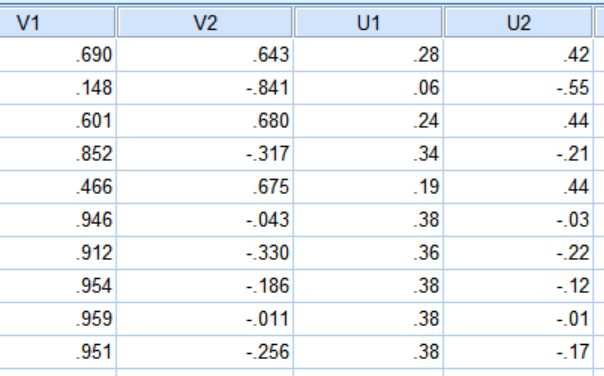
将Ui与10个变量的标准化值相乘即可得到两个主成分Y1、Y2的表达式:

Y1=0.28*X1+0.06X2+0.24X3+0.34X4+0.19X5+0.38X6+0.36X7+0.38X8+0.38X9+0.38X10

Y2=0.42*X1-0.55X2+0.44X3-0.21X4+0.44X5-0.03X6-0.22X7-0.12X8-0.01X9-0.17X10

实验4：因子分析

实验步骤与结果分析：

1.数据准备，在SPSS载入“"D:\桌面\计量地理学实习\因子分析.xlsx"”数据。

2.打开【分析】|【降维】|【因子分析】工具，将数据中除了【城市】这个变量，其余变量全部添加进去，

3.分别点击【描述】、【抽取】和【旋转】中的相关选项，如下图所示：

4.从运行结果上可以看到KMO值为0.762，接近于1，说明这些数据适合进行因子分析。同时Bartlett球形度检验中的Sig值为0.000，小于显著水平0.05，说明变量之间存在相关关系，可以做因子分析。

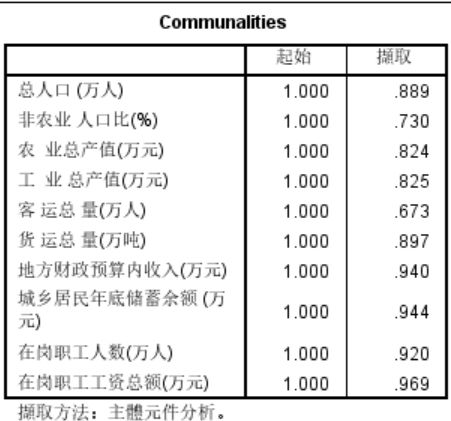
公因子方差最小值为0.73，所有的变量都可以使用公因子进行表达。

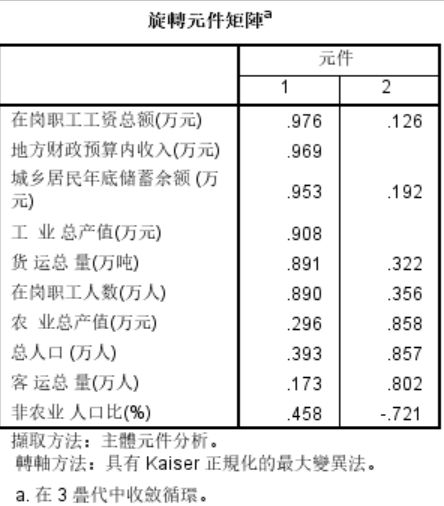
这是旋转成份矩阵。

实验5：聚类分析

实验步骤与结果分析：

1.数据准备，在SPSS载入“"D:\桌面\计量地理学实习\聚类分析.xlsx"”数据。

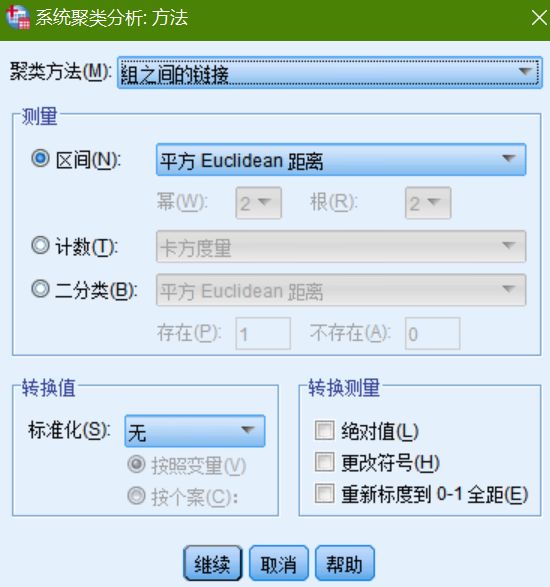
2.打开【分析】|【分类】|【系统聚类】工具，将数据中所有的变量全部添加进去，并且设置相关选项的设置，具体如下图所示：

2.首先给出的是样品处理摘要（CaseProcessingSummary）。摘要告诉我们如下内容：有效样品的数目和百分比，缺失样品的数目和百分比，全部样品的数目和百分比。由于没有数据缺失，故全部21个样本参与聚类，有效样品为100%。

3.从进度表可以看出，第1阶段（Stage1），首先将第12号样品和第13号样品聚为一类，这两个样品的夹角余弦值最大，为623.445。

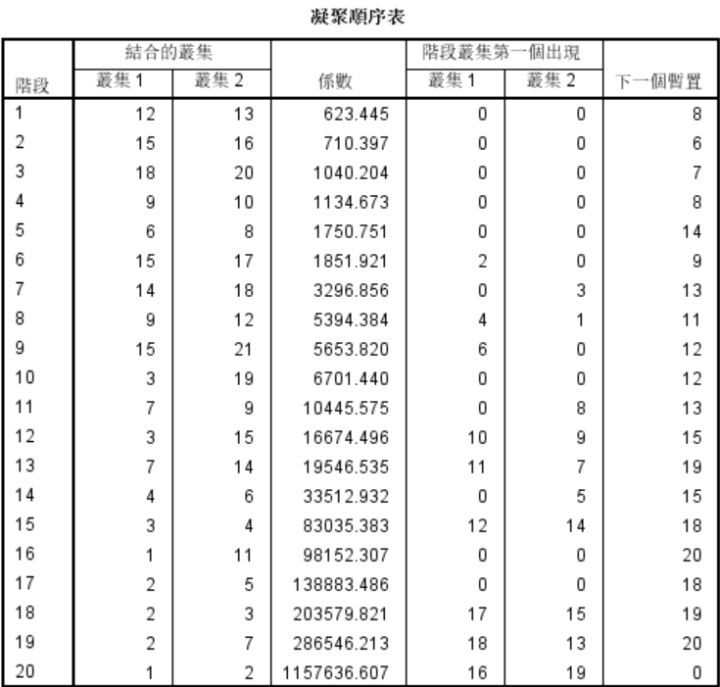
4.根据树形图，选择适当的尺度分为若干类。然后对分类结果进行分析，考察结果是否符合实际。

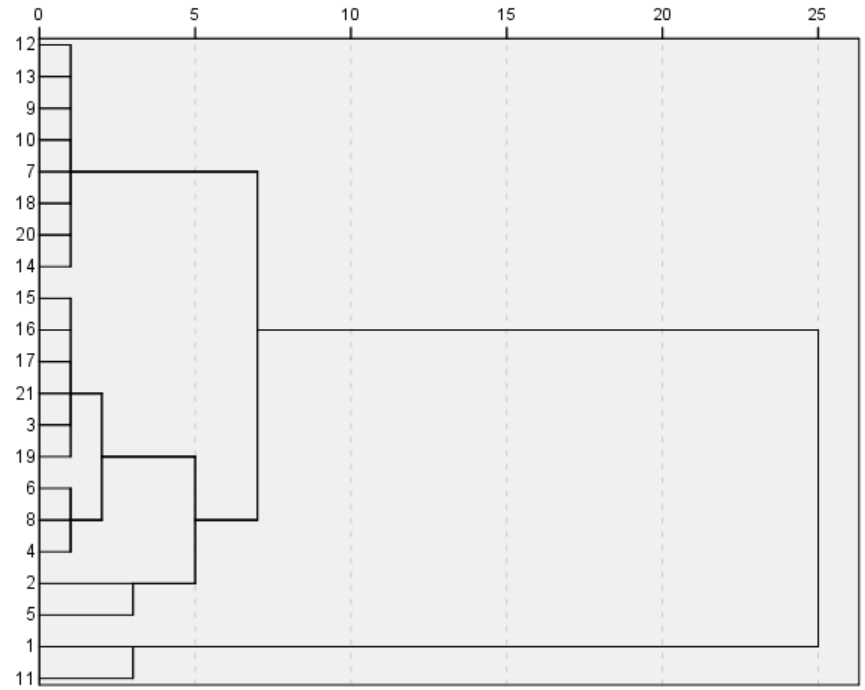
实验6：多元线性回归分析

实验步骤与结果分析：

1.数据准备，在SPSS载入“"D:\桌面\计量地理学实习\多元线性回归分析.xlsx"”数据。

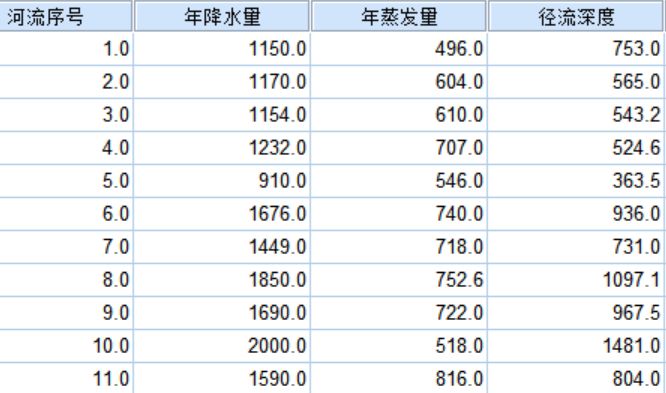
1. 打开【分析】|【回归】|【线性】工具，将数据中所有的变量全部添加进去，并且设置相关选项的设置，具体如下图所示：

3.相关选项设置如下图所示：

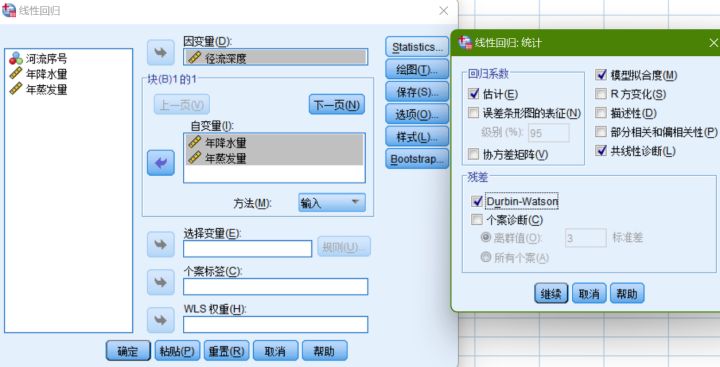
将标准化残差“*ZRESID”选入“Y”中，将标准化预测值“*ZPRED”选入“X”中，勾选直方图和正态概率图，点击继续。

4.结果解读

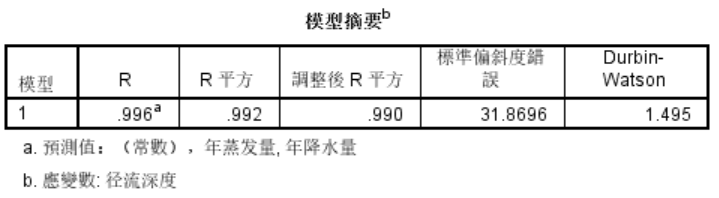
由表可知DW值接近于2，自变量的自相关性不明显，模型设计得好，调整后的R方为0.99，模型拟合度非常好。

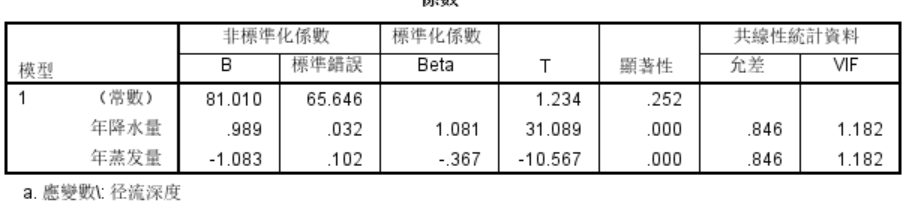
显著性表示自变量对因变量的影响程度，小于0.05表示于显著影响，越小影响越大，由表可以知道年降水量和年蒸发量对径流深度有显著影响。

VIF用于共线性诊断（变量之间的关联度），当0<VIF<10时，不存在多重共线性，由表可知年降水量和年蒸发量之间不存在多重共线性。

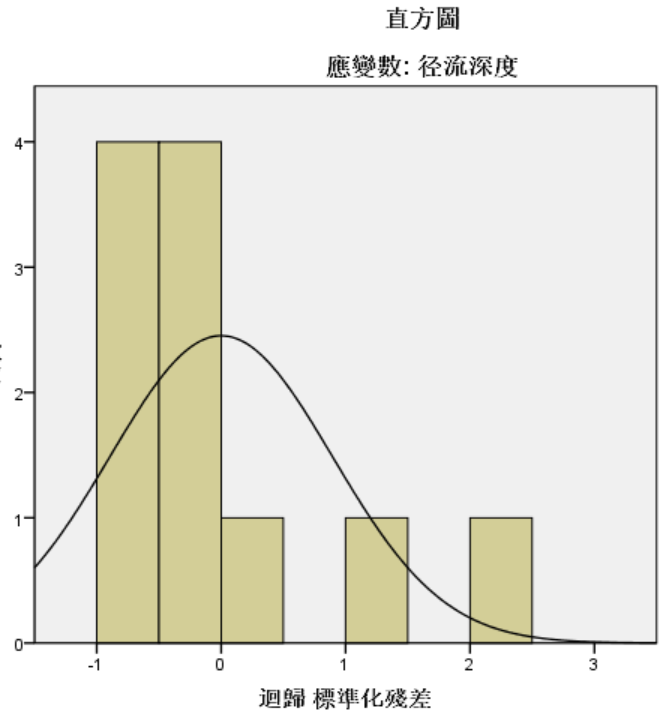
但是根据直方图可以知道直方图和正态曲线较为不吻合，说明残差不符合正态分布。

实验7：马尔可夫分析

实验步骤与结果分析：

1.时间序列数据整理后加载到Excel中，如下图所示：

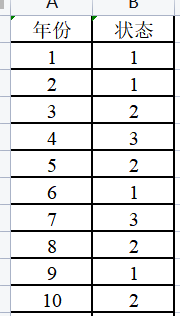
​其中E1、E2和E3分别使用1、2和3代替，年份统一使用1-40代替，

2.为了计算状态的转移矩阵，我使用二维折线图直观显示3个状态随着年份之间的相互转变：

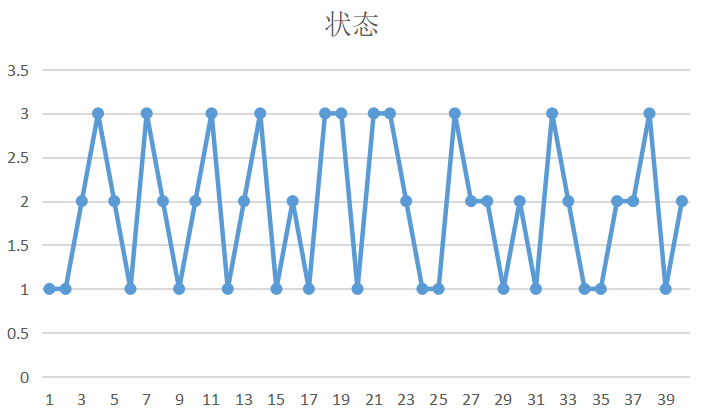
由图可知，

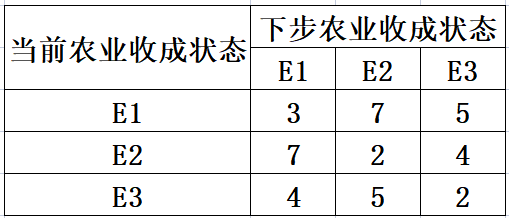
​从而得到初始转移矩阵

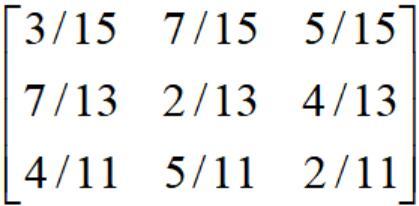
​3.2004年是E2状态，也就是2，预测2030年的农业收成，需要求出26步转移矩阵，为此我们需要计算初始转移矩阵的26次方，如下图所示：

​经过专业软件计算初始转移矩阵的26次方结果为：

4.由于2004年的状态向量为（7/13，2/13，4/13），也就是（0.538，0.154，0.308），求出26年后的状态向量：

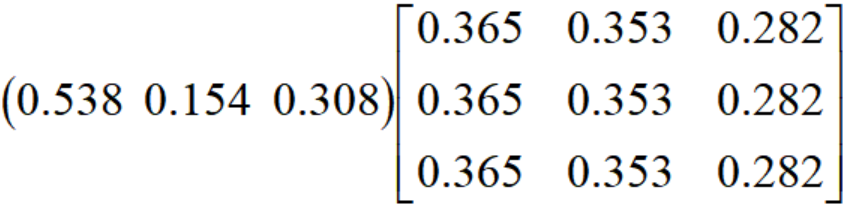
计算结果为（0.365，0.353，0.282），为此可以知道在2030年的农业收成状态大概率是E1（很好）。