- 1webgl开源框架_webgl组态开源
- 2Redis和Mysql如何保证数据一致性?
- 3CL210管理计算资源--红帽的超融合基础设施_red hat超融合
- 4小红书API接口|小红书笔记详情|小红书笔记评论|小红书商品搜索接口|支持高并发|API申请指南
- 5论文阅读 - Toward Mitigating Misinformation and Social Media Manipulation in LLM Era
- 6[转]使用Python scapy构造tcp三次握手,遭遇系统发送rst包解决方法_tcp第三次握手不发ack反而发rst
- 7android大作业快递代拿软件,安卓大作业——校内快递代取app的一些总结
- 8大数据分析:你和月薪50000的程序员差哪了?
- 9SQL中LIKE条件常用的四种模糊查询_sql多个like模糊查询
- 10海思SD3403,SS928/926,hi3519dv500,hi3516dv500移植yolov7,yolov8(4)_sd3403 yolov8
数据结构各内部排序算法总结对比及动图演示(插入排序、冒泡和快速排序、选择排序、堆排序、归并排序和基数排序等)_内部排序算法比较
赞
踩
一、插入排序
插入排序包括直接插入排序,折半插入排序、希尔排序。直接插入排序就是简单粗暴的插入,折半排序是利用了二分查找的插入排序,希尔排序是先局部后整体的插入排序。
其算法的主要思想就是每次将一个待排序的记录按其关键字大小插入到前面已经排好序的子序列,直到全部记录插入完成。
1.直接插入排序
①算法的执行过程:
- 对于待排序表
L[1...n],假设在某个状态下,待排序元素为L(i),则L[1...i-1]为已经排好序的序列,L[i+1...n]为无序序列。 - 将
L(i)依次与L(i-1)...L(1)相比较,找出L(i)在有序序列中要插入的位置k。 - 将
L[k...i-1]中的所有元素依次后移一个位置。 - 将
L(i)复制到L(k)。 i后移,重复2.直到有序序列长度为n
②算法执行过程可视化演示:

③算法代码:
void InsertSort(ElemType A[], int n){
for(int i = 2; i <= n; i++){ //默认首个元素为有序序列,将2~n位置的关键字依次插入
if(A[i] < A[i-1]){ //如果待插入元素小于有序序列最大元素,则需要插入
A[0] = A[i]; //A[0]为“哨兵”,用来存放待插入元素
for(int j = i-1; A[0] < A[j]; j--) //从后往前查找待插入的位置
A[j+1] = A[j]; //依次向后移动
A[j+1] = A[0]; //找到位置之后,将待排序元素插入有序序列
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
④性能分析:
- 空间效率:使用常数个辅助单元,空间复杂度为
O(1) - 时间效率:进行了
n-1趟插入操作,每趟操作都分为比较和移动元素,所以与表的初始状态有关
最好情况下:表已经有序,只需比较不需移动元素,此时时间复杂度为O(n);
最坏情况下:此时为逆序,比较次数为2+3+……+n,总的移动次数为(2+1)+(3+1)+……+(n+1)
平均情况下:出现概率随机,取最好和最坏的平均值,总的比较和移动次数约为(1/4)n2.所以插入排序算法的时间复杂度为O(n2) - 稳定性: 稳定
- 适用性:适用于线性表为顺序存储或链式存储的情况。
2.折半插入排序
①算法的执行过程: 总体过程与上一个类似,只是在寻找插入位置的时候使用的二分查找算法
②算法执行过程可视化演示: 与上一个相同。
③算法代码:
void BinaryInsertSort(ElemType A[], int n){ int low, high, mid; for(int i = 2; i <= n; i++){ //默认首个元素为有序序列,将2~n位置的关键字依次插入 A[0] = A[i]; //A[0]为“哨兵”,用来存放待插入元素 low = 1, high = i-1; while(low <= high){ //low=high时表明查找到要插入的位置 mid = (low+high)/2; //为了保证稳定,相等的情况需要查找右半子表 if(A[mid] > A[0]) high = mid-1; //查找左半子表 else low = mid+1; //查找右半子表 } for(int j = i-1; j >= high+1; j--) //从后往前查找待插入的位置 A[j+1] = A[j]; //依次向后移动 A[high+1] = A[0]; //将待排序元素插入有序序列 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
④性能分析:
- 空间效率:与直接插入排序相同空间复杂度为
O(1) - 时间效率:进行了
n-1趟插入操作,每趟操作都分为比较和移动元素,比较操作与表的初始状态无关,为O(n log2n),移动次数取决于初始状态,所以折半插入排序时间复杂度为O(n2) - 稳定性: 不稳定
- 适用性:仅适用于线性表为顺序存储的情况。
3.希尔排序
希尔排序的由来:当待排序序列为基本有序时,插入排序复杂度可以提高至O(n),所以我们可以让整体基本有序,也就是说部分有序,最后使用插入排序进行排序。由此得出希尔排序,也称缩小增量排序
①算法的执行过程:
- 希尔排序思想即先局部后整体,首先设置增量d,把待排序的表分为k个子表,对每个子表排序后,增量d变为原来的一半,直到减小为d=1.
- 此时的表已经基本有序,进行最后一趟排序之后得到有序序列,这里在每个子表中使用的排序算法仍是插入排序。
②算法执行过程演示:
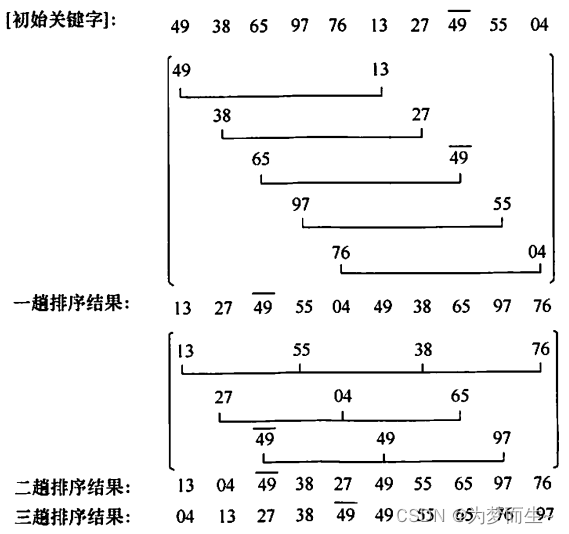
③算法代码:
void ShellSort(ElemType A[], int n){
//通过增量d把序列分为多个子表,外层for循环控制增量的变化
for(int dk = n/2; dk >= 1; dk /= 2){
//对于每一个增量得到的子表进行插入排序
for(int i = dk+1; i <= n; i++){
if(A[i] < A[i-dk]){ //如果待插入元素小于有序序列最大元素,则需要插入
A[0] = A[i]; //将元素暂存到A[0],但在这里并没有起到哨兵的作用
for(int j = i-dk; j > 0 && A[0] < A[j]; j -= dk)
A[j+dk] = A[j]; //依次向后移动
A[j+dk] = A[0]; //将待排序元素插入有序序列
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
④性能分析:
- 空间效率:使用常数个辅助单元,空间复杂度为
O(1) - 时间效率:由于希尔排序的复杂度依赖增量序列的函数,所以时间复杂度分析比较困难。当n在某个特定范围时,其时间复杂度为O(n1.3),最坏情况下为O(n2)。
- 稳定性:不稳定
- 适用性:仅适用于线性表为顺序存储的情况。
二、交换排序
此类排序是根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。
1.冒泡排序
①算法的执行过程:
- 冒泡排序是一种基于比较的简单交换排序,会进行多轮交换,在每趟排序中,从后往前两两比较相邻元素的值,若为逆序,则交换他们。
- 在每趟排序完成后,都会将当前待排序序列中最小的元素放到第一个位置(或最大的元素放到最后一个位置)。
- 最多进行
n-1趟处理后,所有元素就能排好。第i趟排序要进行n-i次比较。
②算法执行过程可视化演示:

③算法代码:
void BubbleSort(ElemType A[], int n){
for(int i = 0; i < n-1; i++){ //一共n-1趟
for(int j = 0; j < n-1-i; j++){ //对应每一趟的比较
if(A[j] > A[j+1]){ //若为逆序则交换
swap(A[j], A[j+1]);
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
④性能分析:
- 空间效率:使用常数个辅助单元,空间复杂度为
O(1) - 时间效率:最好情况下时间复杂度为O(n),最坏情况下初始为逆序,需要n-1趟排序,第i趟需要n-i次关键字的比较,每次比较都需要移动元素3次来交换元素位置,所以最坏情况和平均情况复杂度都为O(n2).
- 稳定性:稳定
- 适用性:适用于线性表为顺序存储和链式存储的情况。
拓展(链式存储的冒泡排序):
void sort_list(PNODE pHead){
int i,j,t;
PNODE p, q;
int len= length_list(pHead);
for (i=0,p=pHead->pNext;i<len-1;++i,p=p->pNext){
for (j=i+1,q=p->pNext;j<len;++j,q=q->pNext){
if (p->data > q->data){
t = p->data;
p->data = q->data;
q->data = t;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
2.快速排序
①算法的执行过程:
- 快速排序是一种基于分治思想的交换排序
- 在待排表
L[1...n]中任取一个元素pivot作为枢轴(或基准) - 通过一趟排序将待排序表划分为两个部分,
L[1...k-1]和L[k+1...n],使得L[1...k-1]中所有元素小于pivot,L[k+1...n]中所有元素大于pivot。 - 此时的枢轴元素privot已经放到了最终的位置上。
- 递归的对两个子表重复以上步骤,直到每个子表只有一个元素或为空。
②算法执行过程演示:

③算法代码:
//划分操作 int Partition(ElemType A[], int low, int high){ ElemType pivot = A[low]; //定义第一个元素为枢轴元素 while(low < high){ while(low < high && A[high] > pivot) high--; A[low] = A[high]; //从后往前找到第一个小于枢轴的元素放到左边 while(low < high && a[low] < pivot) low++; A[high] = A[low]; //从前往后找到第一个大于枢轴的元素放到右边 } A[low] = pivot; //将枢轴元素放到最终的位置 return low; //返回枢轴元素的位置 } //递归的进行快排 void QuickSort(ElemType A[], int low, int high){ if(low < high){ //如果两个指针的位置相反或者相等,表明递归结束 int pos = Partition(A, low, high); //找到枢轴元素的位置 QuickSort(A, low, pos-1); //递归排序左子表 QuickSort(A, pos+1, high); //递归排序右子表 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
④性能分析:
- 空间效率:由于快排是递归的,所以空间复杂度与递归深度有关。
二分递归空间复杂度最好情况下为O(log2n),最坏情况下进行n-1次调用,深度为O(n) - 时间效率:与划分的好坏有关
最坏情况下:每层递归都是最大限度的不对称(两个区域分别包含n-1和0个元素),复杂度为O(n2)也就是对应初始排序表基本有序或基本逆序。
最理想情况:每层递归能能完美的划分,复杂度为O(nlog2n)。得到的两个子问题规模都小于n/2。 - 稳定性:不稳定
- 适用性:适用于线性表为顺序存储的情况。
三、选择排序
每一趟在后面
n-i-1个元素中选取最小的元素,作为有序序列的第i个元素,直到第n-1趟排序完成。最重要的还是堆排序。
1.简单选择排序
①算法执行过程可视化演示:

②算法代码:
void SelectSort(ElemType A[], int n){
for(int i = 0; i < n-1; i++){ //一共进行n-1趟
int min = i; //记录最小元素的位置
for(j = i+1; j < n; j++) //在待排序表中找到最小的元素
if(A[j] < A[min]) min = j; //更新最小元素下标
if(min != i) swap(A[i], A[min]);//交换位置
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
③性能分析:
- 空间效率:使用常数个辅助单元,复杂度为O(1)。
- 时间效率:元素比较次数与初始状态无关,为n(n-1)/2次,移动次数最多为3(n-1)最少为0次,时间复杂度为O(n2)
- 稳定性:不稳定
2.堆排序
堆的定义: 满足n个关键字序列
L[1...n]称为堆,堆可分为大根堆和小根堆,其在逻辑结构上可视为一棵完全二叉树。
如果满足每个结点的值都大于其左孩子和右孩子结点的值,则是大根堆;
如果满足每个结点的值都小于其左孩子和右孩子结点的值,则是小根堆。
①算法的执行过程:
- 首先将存放在表中的元素建成初始堆
- 输出堆顶元素,末尾元素补位
- 调整堆使其保持特性
- 重复以上步骤至所有元素都已输出
堆排序核心问题:①如何建堆;②输出元素后如何调整。
②算法执行过程可视化演示:
- 大根堆建堆
①从最后一个分支结点开始,与其孩子结点的值比较。如果不符合特性,则交换;如果是大根堆,选择孩子结点中的较大值,否则选择最小值;
②交换之后如果孩子结点也是分支结点,继续向下比较;
③反复利用上述过程构造下一级的堆,直至根结点。
- 输出
①输出堆顶元素后,将最后一个元素与之交换;
②此时堆的结构特性被破坏,需要向下筛选;
③从上向下逐级比较,使每一级都符合特性。

除了以上的主要功能,堆还具有以下的作用:
- 插入

- 更新

③算法代码:
//大根堆的建立 void BuildMaxHeap(ElemType A[], int len){ //从最后一个分支结点开始,逐级向上建堆 for(int i = len/2; i > 0; i--) HeapAdjust(A, i, len); } void HeapAdjust(ElemType A[], int k, int len){ A[0] = A[k]; //暂存这个分支结点 for(int i = 2*k; i <= len; i *= 2){ //从这个分支结点开始向下调整 if(i < len && A[i] < A[i+1]) i++; //右孩子更大 if(A[0] >= A[i]) break; //分支结点已是子堆中的最大值,符合特性 else{ //不符合特性,需要调整 A[k] = A[i]; //换的时候只是覆盖 k = i; //下标要交换,下次还说与A[0]比较 } } A[k] = A[0]; //放到最终符合特性的位置上 } //堆排序 void HeapSort(ElemType A[], int len){ BuildMaxHeap(A, len); //建堆 for(int i = len; i > 1; i--){ //n-1趟交换和建堆过程 swap(A[i], A[1]); //堆顶元素和堆底元素互换 HeapAdjust(A, 1, i-1); //将剩余的元素调整 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
④性能分析:
- 空间效率:使用常数个辅助单元,空间复杂度为
O(1) - 时间效率:建堆时间为O(n),之后有n-1次向下调整,调整操作的时间复杂度为O(h)也就是O(log2n),所以堆排序的时间复杂度为O(nlog2n)。
- 稳定性:不稳定
- 适用性:适用于线性表为顺序存储的情况。
四、归并排序
归并排序与之前的算法思想不一样,它是将两个或以上的有序子表组合成一个新的有序表的过程。
我们称之为分治思想,在之前的快速排序中也有所体现。
①算法的执行过程:
- 对于n个元素的k路归并
- 首先可以开辟一块与表长度相同的辅助数组
- 分解: 将n个元素的待排序表分成各含n/2个元素的子表,每个表为长度为h的有序段。将每个子表进行递归的划分;
- 合并:每次归并时,将前后相邻且长度为h的有序段进行两两归并,得到前后相邻,长度为2h的有序段;
- 经过logkn次排序之后整个表变为有序表
②算法执行过程可视化演示:

③算法代码:
ElemType *B = (ElemType*)malloc((n+1)*sizeof(ElemType)); //辅助数组B void Merge(ElemType A[], int low, int mid, int high){ // for(int k = low; k <= high; k++) B[k] = A[k]; //将A的所有元素复制到B for(int i = low, j = mid+1, k = i; i <= mid && j <= high; k++){ //将两个子表归并成一个有序表 if(B[i] <= B[j]) A[k] = B[i++]; //小元素放到前面,指针后移 else A[k] = B[j++]; } while(i <= mid) A[k++] = B[i++]; //将A中剩余的元素复制到B while(i <= high) A[k++] = B[j++]; } void MergeSort(ElemType A[], int low, int high){ if(low < high){ int mid = (low+high)/2; //从中间划分两个子序列 MergeSort(A, low, mid); //对左子表进行递归的排序 MergeSort(A, mid+1, high); //对右子表进行递归的排序 Merge(A, low, mid, high); //最后将两个序列归并到一起 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
④性能分析:
对于2路归并排序算法的性能分析如下:
- 空间效率:使用n个辅助单元,空间复杂度为
O(n) - 时间效率:每趟递归的时间复杂度为O(n),一共需要log2n次归并,所以总的时间复杂度为O(nlog2n)
- 稳定性:稳定
- 适用性:适用于线性表为顺序存储的情况。
五、基数排序
基数排序是一种很特别的排序,它不基于比较和移动,而是基于各个位上关键字的大小进行排序。
假设长度为n的线性表由d元组(kjd-1, kjd-2, …, kj1, kj0)组成,其中kjd-1为最主位关键字,kj0为最次位关键字。
关键字排序有两种方法:
①最高位优先法:按关键字权重递减依次逐层划分成子序列,然后依次连接成有序序列。
②最低位优先法:按关键字权重递增依次逐层划分成子序列,然后依次连接成有序序列。
①算法的执行过程:
- 确定执行的轮数:确定数组中的最大元素有几位
- 创建编号为0-9的9个队列,因为所有的数字元素都是由0~9的十个数字组成
- 依次判断每个元素的个位,十位直至d位,根据相应数字存入对应的队列中
- 当表中的元素都放完后,依次出队,存入原数组,直至MAX轮结束输出数组。
②算法执行过程可视化演示:

由于基数排序较为复杂且变化形式多样,这里的总结文章将不会给出代码
③性能分析:
- 空间效率:排序过程中使用
r个队列,所以基数排序的空间复杂度为O(r) - 时间效率:根据位数的多少,基数排序会进行d趟分配和收集。分配的时间与长度
n呈线性关系,收集与队列的多少r有关,分别为O(n)和O(r)。所以基数排序的时间复杂度为O(d(n+r)),且与线性表的初始状态无关。 - 稳定性:稳定
- 适用性:适用于线性表为顺序存储和链式存储的情况。
六、对比总结
1.从时间复杂度看
- 平均情况下的时间复杂度为O(n2)的算法有:简单选择排序、直接插入排序和冒泡排序。(但直接插入排序和冒泡排序最好情况下的时间复杂度可以达到O(n),而简单选择排序则与序列的初始状态无关)
- 平均情况下的时间复杂度为O(nlog2n)的算法有:快速排序、堆排序、归并排序。(快速排序基于分治的思想,虽然最坏情况下快速排序时间会达到O(n2),但快速排序平均性能可以达到(nlog2n),在实际应用中常常优于其他排序算法。归并排序同样基于分治的思想,但由于其分割子序列与初始序列的排列无关,因此它的最好、最坏和平均时间复杂度均为O(nlog2n)。堆排序利用了一种称为堆的数据结构,可在线性时间内完成建堆)
- 希尔排序作为插入排序的拓展,对较大规模的排序都可以达到很高的效率,但目前未得出其精确的渐近时间。
- 基数排序与其他的都不同,它的最好、最坏和平均时间复杂度均为O(d(n+r))。
2.从空间复杂度看
- 简单选择排序、插入排序、冒泡排序、希尔排序和堆排序都仅需要借助常数个辅助空间。
- 快速排序在空间上只使用一个小的辅助栈,用于实现递归,平均情况下大小为O(log2n),当然在最坏情况下可能会增长到O(n)。
- 2路归并排序在合并操作中需要借助较多的辅助空间用于元素复制,大小为O(n)(虽然有方法能克服这个缺点,但其代价是算法会很复杂而且时间复杂度会增加)
3.从稳定性看
- 插入排序、冒泡排序、归并排序和基数排序是稳定的排序方法
- 简单选择排序、快速排序、希尔排序和堆排序都是不稳定的排序方法
4.从过程特征看
- 采用不同的排序算法,在一次循环或几次循环后的排序结果可能是不同的
- 冒泡排序和堆排序在每趟处理后都能产生当前的最大值或最小值
- 快速排序一趟处理就能确定一个元素的最终位置
5.性质对比
| 算法种类 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| \ | 最好情况 —平均情况—最坏情况 | \ | \ |
| 直接插入排序 | O(n)------O(n2)------O(n2) | O(1) | 是 |
| 冒泡排序 | O(n)------O(n2)------O(n2) | O(1) | 是 |
| 简单选择排序 | O(n2)------O(n2)------O(n2) | O(1) | 否 |
| 快速排序 | O(log2n)—O(log2n)—O(n2) | O(log2n) | 否 |
| 堆排序 | O(log2n)—O(log2n)—O(log2n) | O(1) | 否 |
| 二路归并排序 | O(log2n)—O(log2n)—O(log2n) | O(n) | 是 |
| 基数排序 | O(d(n+r))—O(d(n+r))—O(d(n+r)) | O( r ) | 是 |



