『初阶数据结构 • C语言』⑥ - 插入排序&希尔排序_乐观排序算法

学习目标

写在前面

1.插入排序

2.插入排序实战 

3.插入排序的实现 

4.插入排序的效率

5.平均情况

6.希尔排序

7.希尔排序的实现

8.希尔排序的效率

9.总结 

---

写在前面

之前我们衡量一个算法的效率时，都是着眼于它在最坏情况下需要多少步。原因很简单，连最坏的情况都做足准备了，其他情况自然不在话下。

但是，在我们实际生活中并不总是面临最坏情况，更多的是平均情况。本章我们会见证一种自适应性极强的排序算法---希尔排序，还有它的组成它的关键---插入排序。

---

1.插入排序

我们已经学过两种排序算法：冒泡排序和选择排序。虽然它们的效率都是 O(N^2 )，但其实选择排序比冒泡排序快一倍。

现在来学第三种排序算法——插入排序（直接插入排序）。你会发现，顾及最坏情况以外的场景将是多么有用。插入排序包括以下步骤。

插入排序包括以下步骤。

(1) 在第一轮里，暂时将索引 1（第 2格）的值移走，并用一个临时变量来保存它。这使得该索引处留下一个空隙，因为它不包含值。

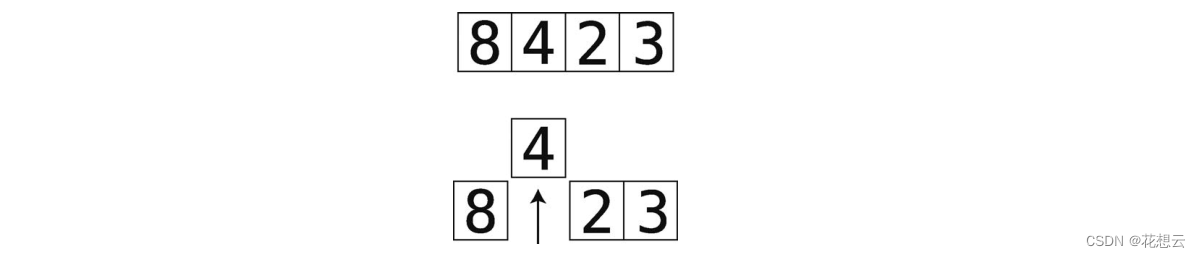
 在之后的轮回，我们会移走后面索引的值。

(2) 接着便是平移阶段，我们会拿空隙左侧的每一个值与临时变量的值进行比较。

如果空隙左侧的值大于临时变量的值，则将该值右移一格。 

随着值右移，空隙会左移。如果遇到比临时变量小的值，或者空隙已经到了数组的最左端，就结束平移阶段。 

(3) 将临时移走的值插入当前空隙。

(4) 重复第(1)至(3)步，直至数组完全有序。

---

2.插入排序实战 

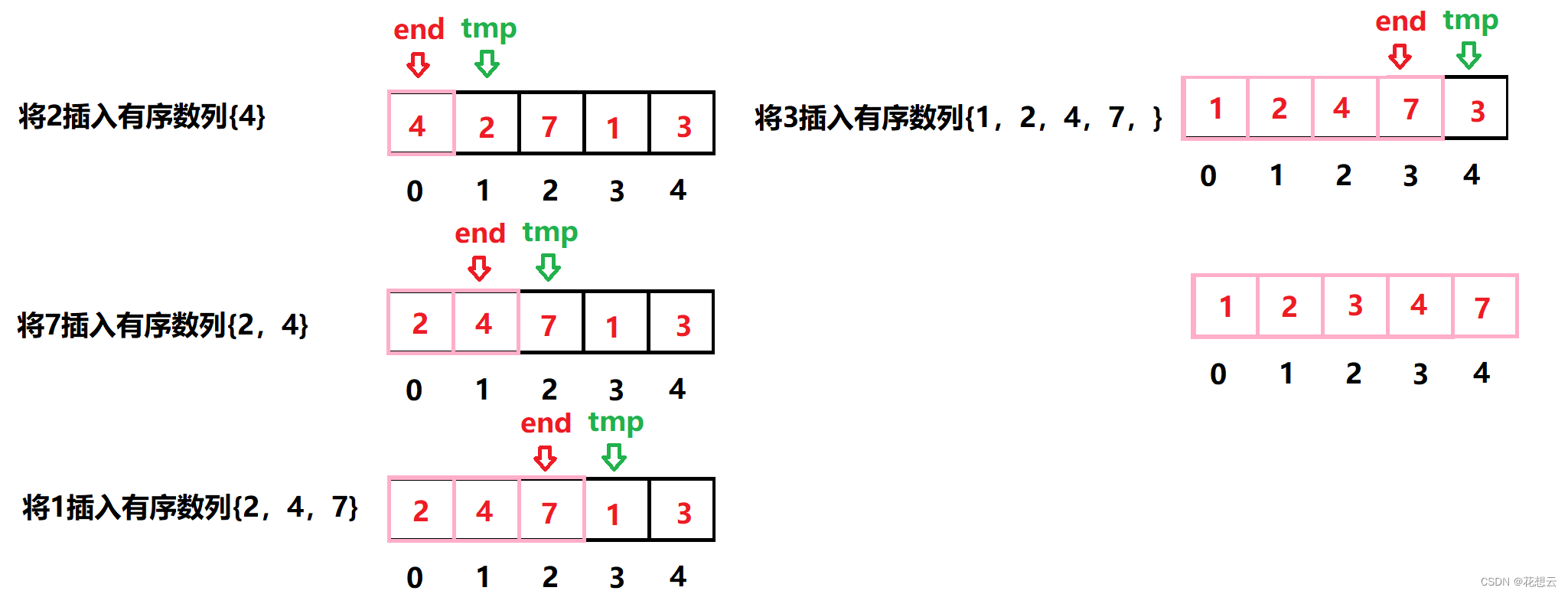
下面尝试对 [4, 2, 7, 1, 3] 数组运用插入排序。

第 1轮先从索引 1开始，其值为 2。

准备工作：暂时移走 2，并将其保存在变量 tmp 中。图中被移到数组上方的就是
tmp。 

 第 1步：比较 4与 tmp中的 2。

第 2步：因为 4大于 2，所以把 4右移。

 于是空隙移到了数组最左端，没有其他值可以比较了。

 第 3步：将 tmp插回数组，完成第一轮。

开始第 2轮。

准备工作：暂时移走索引 2的值，并保存到 tmp中。于是 tmp等于 7。

第 4步：比较 4与 tmp。

4小于 7，所以无须平移。因为遇到了小于 tmp的值，所以平移阶段结束。

第 5步：将 tmp插回到空隙中，结束第 2轮。

开始第 3轮。

准备工作：暂时移走 1，并将其保存到 tmp中。

 第 6步：比较 7与 tmp。

 第 7步：7大于 1，于是将 7右移。

 第 8步：比较 4与 tmp。

第 9步：4大于 1，于是也要将 4右移。 

第 10步：比较 2与 tmp。

第 11步：2比较大，所以将 2右移。

第 12步：空隙到了数组最左端，因此我们将 tmp插进去，结束这一轮。 

开始第 4轮。

准备工作：暂时移走索引 4的值 3，保存到 tmp中。

第 13步：比较 7和 tmp。

 第 14步：7更大，于是将 7右移。

第 15步：比较 4与 tmp。

第 16步：4大于 3，所以将 4右移。

第 17步：比较 2与 tmp。2 小于 3，于是平移阶段完成。

 第 18步：把 tmp插回到空隙。

 至此整个数组都排好序了。

---

3.插入排序的实现 

以下使用C语言实现的直接插入排序：

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (a[end] > tmp)         //大于tmp，往后挪一个
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;          //把tmp插入空隙
	}
}

 让我们一步步来讲解：

for (int i = 0; i < n - 1; i++)

 最外层的这个循环用来控制end的位置，也就是一个轮回。

		int end = i;
		int tmp = a[end + 1];

我们通过控制end的位置，使end与end之前的数列都是有序的，而把end+1索引处的值（也就是tmp）插入到end之前的数列中。所以，end的值是从0开始的。这样能保证end与end之前的数列是有序的（因为只有一个数），那么将tmp插入后，前end+1个数都是有序的，再依次执行下去。

while (end >= 0)

end索引处的值会发生移动，最坏的情况是tmp的值比之前的有序数列中每一个值都要小，那么空隙的位置就在end=0处。例如：

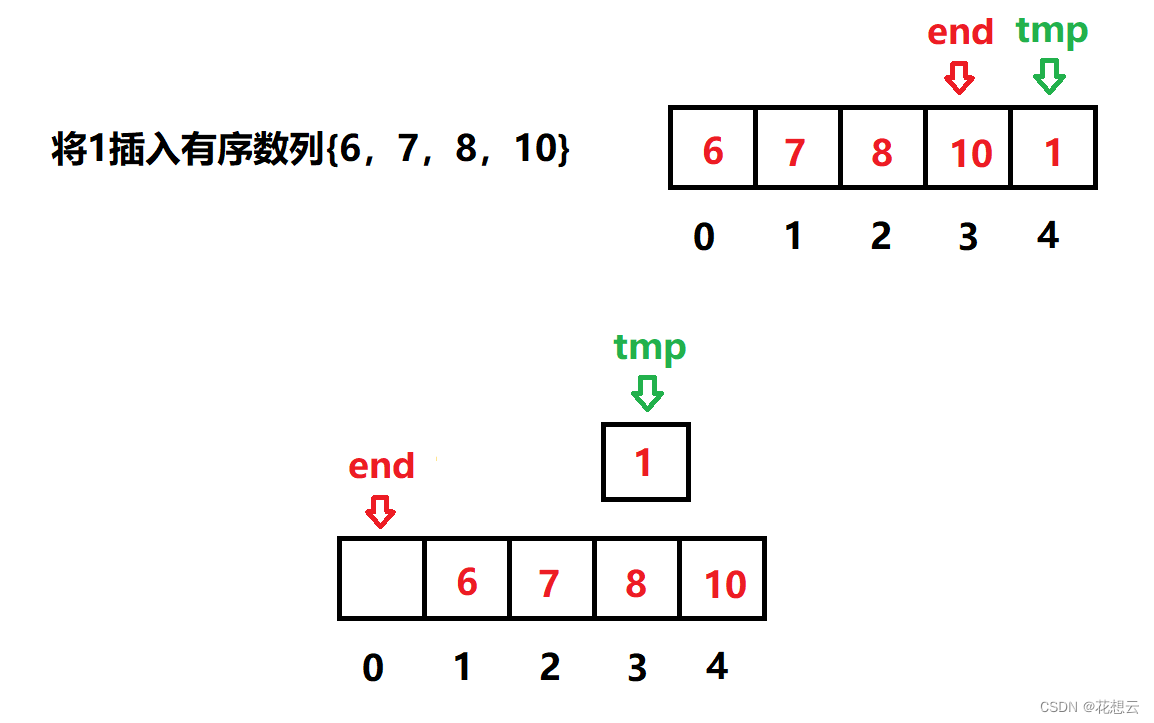
            if (a[end] > tmp)         //大于tmp，往后挪一个
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}

找到空隙，将比tmp大的数字不断往后挪，直到找到小于等于tmp的数字。

a[end + 1] = tmp;          //把tmp插入空隙

将tmp插入空隙。

---

4.插入排序的效率

插入排序包含 4种步骤：移除、比较、平移和插入。要分析插入算法的效率，就得把每种步骤都统计一遍。

首先看看比较。每次拿 tmp跟空隙左侧的值比大小就是比较。

在数组完全逆序的最坏情况下，我们每一轮都要将 tmp左侧的所有值与tmp比较。因为那些值全都大于 tmp，所以每一轮都要等到空隙移到最左端才能结束。

对于含有N个元素的数组，可以得出比较的总次数为：

1 + 2 + 3 + … + N - 1 次。

接下来看看其他几种步骤。

我们每次将值右移一格，就是平移操作。当数组完全逆序时，有多少次比较就要多少次平移，因为每次比较的结果都会使你将值右移。

因而可以得出平移的总次数为：

1 + 2 + 3 + … + N - 1 次。

tmp的移除跟插入在每一轮里都会各发生一次。因为总是有 N - 1轮，所以可以得出结论：有 N - 1次移除和 N - 1次插入。

把它们都相加。

N^2 比较和平移的合计
+ N - 1 次移除
+ N - 1 次插入
=
N^2 + 2N - 2步

我们已经知道大 O有一条重要规则——忽略常数，于是你可能会将其简化成 O(N^2 + N)。不过，现在来学习一下大 O的另一条重要规则：

大 O 只保留最高阶的 N。

换句话说，如果有个算法需要 N^4 + N^3 + N^2 + N步，我们就只会关注其中的 N^4 ，即以 O(N^4 )
来表示。为什么呢？

请看下表。

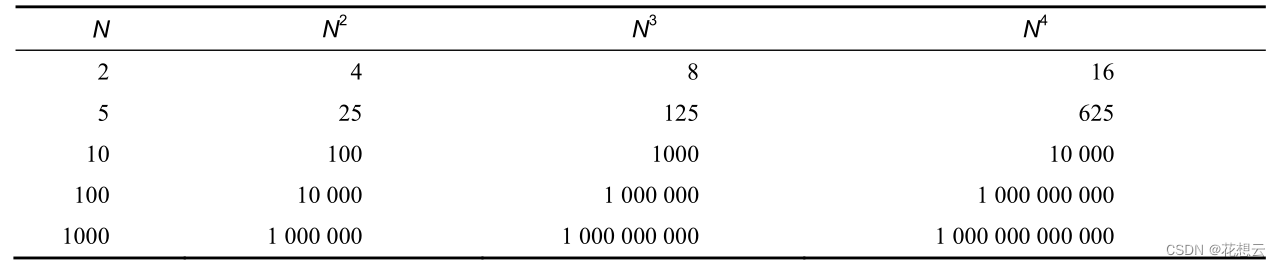
随着 N的变大，N^4 的增长越来越抛离其他阶。当 N为 1000时，N^4 就比 N^3 大了 1000倍。因
此，我们只关心最高阶的 N。
所以在插入排序的例子中，O(N^2 + N)还得进一步简化成 O(N^2 )。

不过上一章曾指出，虽然冒泡排序和选择排序都是 O(N^2 )，但选择排序实际上是 N^2 / 2步，
比 N 2 步的冒泡排序更快。乍一看，你可能会觉得插入排序跟冒泡排序一样，因为它们都是 O(N^2 )，其实插入排序是 N^2 + 2N - 2步。你或许会认为比冒泡排序和插入排序快一倍的选择排序是三者中最优的，但事情并没有这么简单。

---

5.平均情况

确实，在最坏情况里，选择排序比插入排序快。但是我们还应该考虑平均情况。

最好情况和最坏情况很少发生。现实世界里，最常出现的是平均情况。

这是很有道理的。你设想一个随便洗乱的数组，出现完全升序或完全降序的可能性有多大？最可能出现的情况应该是随机分布。

下面试试在各种场景中测试插入排序。

完全降序的最坏情况之前已经见过，它每一轮都要比较和平移所遇到的值（这两种操作合计N^2 步）。

对于完全升序的最好情况，因为所有值都已在其正确的位置上，所以每一轮只需要一次比较，完全不用平移。

最坏情况是所有数据都要比较和平移；最好情况是每轮一次比较、零次平移；对于平均情况，总的来看，是比较和平移一半的数据。

如果说插入排序的最坏情况需要 N 2 步，那么平均情况就是 N 2 / 2步。尽管最终大 O都会写成 O(N^2 )。

可以看到插入排序的性能在不同场景中差异很大。最坏、平均、最好情况，分别需要 N^2 、
N^2 / 2、N步。

那么哪种算法更好？选择排序还是插入排序？答案是：看情况。对于平均情况（数组里的值随机分布），它们性能相近。如果你确信数组是大致有序的，那么插入排序比较好。如果是大致逆序，则选择排序更快。

---

6.希尔排序

希尔排序是对插入排序做了简单的优化，却产生了质的飞跃。直接让不太起眼的插入排序比肩闻名算法界的快速排序。我们知道对于插入排序，数据的元素越是接近有序，那么它的效率就越高；对于完全有序的数组，它甚至可以快到O(N)。

那么希尔排序的主要思想是，我们不断地对数组进行预排序，使数组里大的元素尽量到数组的后面，小的元素尽量到数组的前面。

完成对数组的预排序看，我们采取的方法是对数组进行分组，把数组里间隔相同长度的元素划分为一组。例如：

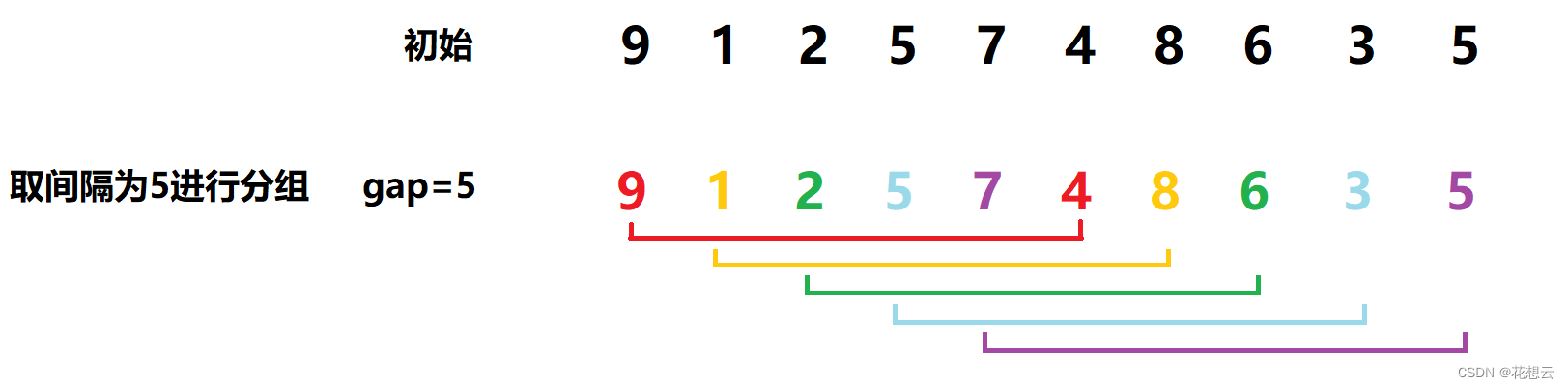
 接下来我们对每一组的元素进行排序。

如图所示，第一趟排序，较大的元素已经到了数组的后面了。接下来再次重新分组，再次预排序：

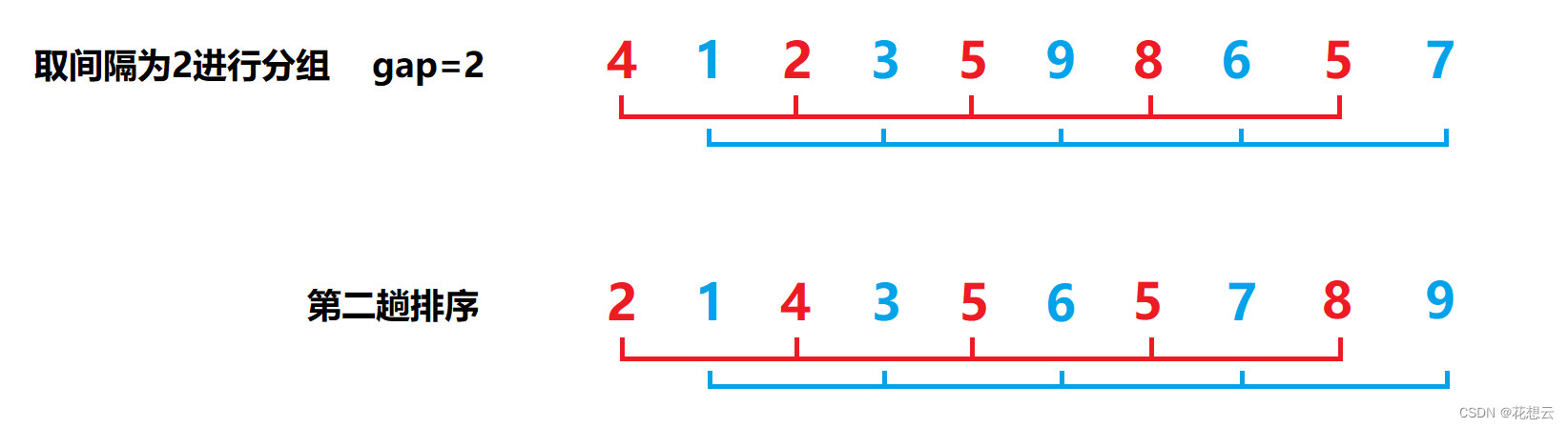
经过第二趟预排序，我们发现数组已经大致接近有序了，那么最后一次，我们取间隔为1分组，其实就是一次普通的插入排序：

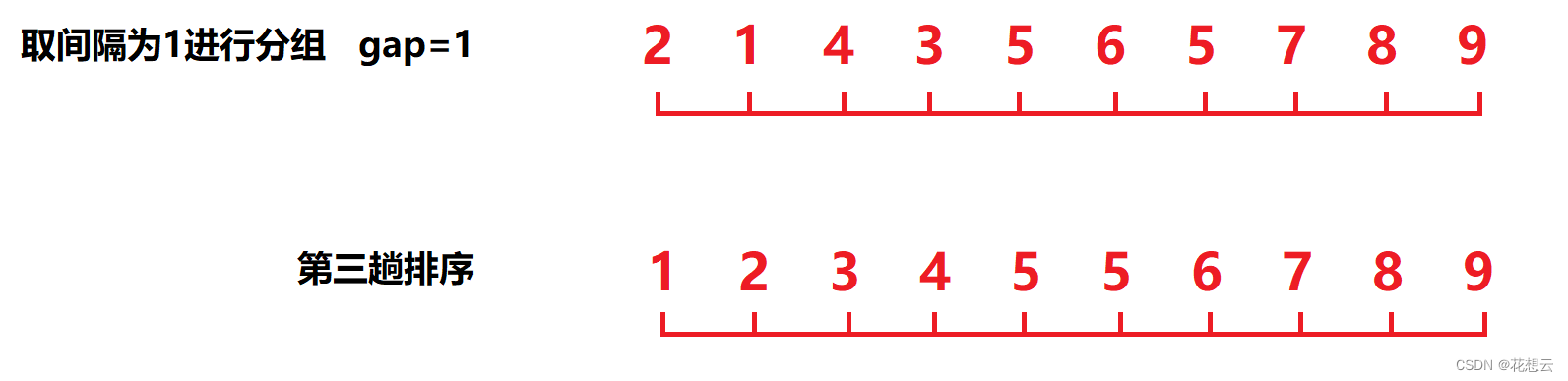
至此，数组已经完全有序了。

通过上面的例子不难看出，希尔排序就是对插入排序的简单优化，引入了预排序的概念。

当gap>1时，进行的是预排序（也就是对每一组进行插入排序）；

当gap=1时，进行对整个数组的插入排序。

---

7.希尔排序的实现

下面使用C语言实现的希尔排序：

void ShellSort(int* a, int n)
{
	int gap = n;             //间隔
	while (gap > 1)
	{
		gap = gap / 3 + 1;   //+1是为了使gap最后等于1
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

代码相较于插入排序并没有改变多少，在插入排序的基础上多了一层循环用来控制gap。

此处可以看出，预排序并不是固定的3次或者4次。而是取决于数组元素个数，这么做一是为了方便控制gap，二是预排序越多次，对整体排序而言更有利，所以我们不用吝啬预排序，并不是预排序越多，花费的步数就越多，时间复杂度就越高。

gap = gap / 3 + 1; 

除了这样控制gap外，还有一种常用的方法：

gap = gap / 2; 

但是根据有人实验得出，第一种方式比第二种方式快一点点，但是差距很细微，所以两者皆可。

---

8.希尔排序的效率

希尔排序的时间复杂度并不好算，因为每次取gap的值都不同，而且gap取不同值的情况下，每次预排序所面临的数据也不同。希尔排序的时间复杂度计算需要运用到数学知识，而且目前为止我们也没有得到严格的标准答案。有人在大量实验的基础上得出希尔排序的时间复杂度接近O(N^1.3)。

《数据结构(C语言版)》--- 严蔚敏

 《数据结构-用面相对象方法与C++描述》--- 殷人昆

因为我们的gap取值的方式是按照Knuth的方式取的，所以以我们这种方式实现的希尔排序时间复杂度暂定为O(N^1.25)。

目前仅仅靠时间复杂度的对比，我们也许感受不到什么叫做质的飞跃，那我们就通过一组数据来对比一下二者的差距。

这是一个测试排序算法所用时间的函数：

void TestOP()
{
	srand(time(0));
	const int N = 1000000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
 
	int j = 0;
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	printf("%d\n", j);
 
	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();
 
	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();
 
	int begin3 = clock();
	//SelectSort(a3, N);
	int end3 = clock();
 
	int begin4 = clock();
	//HeapSort(a4, N);
	int end4 = clock();
 
	int begin7 = clock();
	//BubbleSort(a7, N);
	int end7 = clock();
 
	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();
 
	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();
 
	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("BubbleSort:%d\n", end7 - begin7);
 
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
 
	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
}

我们以排序1百万个元素为例，得到以下结果：

 很显然两种排序算法已经不在一个数量级了。

---

9.总结

懂得区分最好、平均、最坏情况，是为当前场景选择最优算法以及给现有算法调优以适应环境变化的关键。记住，虽然为最坏情况做好准备十分重要，但大部分时间我们面对的是平均情况。