力扣300题

现在开始刷力扣题。这里记录不会的题
https://leetcode.cn

665.非递减数列(第三遍没写出来)

总结思想：利用贪心算法，当i>i+1时，要不缩小i的值到i+1，要不放大i+1的值到i，并且保证尽量不放大i+1的值。

总结：这种数组考虑顺序（递增）的题，在纸上画向上的箭头理解。

724.寻找数组的中心下标(第三遍写出来了)

思路：前缀和：当遍历到i时，左侧sum_l = 右侧total-sum_l-nums[i]，若相等就返回

747.至少是其他数字两倍的最大数(第三遍写出来了)
能否一次遍历完成？

LCP 66.最小展台数量(第三遍写出来了)
不算难

1. 贪心算法

顾名思义，贪心算法或贪心思想采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

举一个最简单的例子：小明和小王喜欢吃苹果，小明可以吃五个，小王可以吃三个。已知苹 果园里有吃不完的苹果，求小明和小王一共最多吃多少个苹果。在这个例子中，我们可以选用的 贪心策略为，每个人吃自己能吃的最多数量的苹果，这在每个人身上都是局部最优的。又因为全 局结果是局部结果的简单求和，且局部结果互不相干，因此局部最优的策略也同样是全局最优的 策略。

怎么知道能不能用贪心？
  最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。

个人总结：在使用贪心算法的时候，需要想好贪心算法的策略：保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

分配问题：

455 Assign Cookies (Easy)

135 分发糖果（第二遍没做出来）
大体思路没错，小问题不断。

435 无重叠区间(第二遍难，看答案才做出来)

452 用最少数量的箭引爆气球（第二遍没做）

406 根据身高重建队列（第二遍没做）
一般这种数对，还涉及排序的，根据第一个元素正向排序，根据第二个元素反向排序，或者根据第一个元素反向排序，根据第二个元素正向排序，往往能够简化解题过程。

---

代码随想录：
376.摆动序列
53.最大子数组和（第二遍没做出来，看答案才会做）

• 分析：关键在于：不能让“连续和”为负数的时候加上下一个元素，而不是 不让“连续和”加上一个负数。这块真的需要仔细体会！

45.跳跃游戏 II

2. 玩转双指针

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多

个数组的多个指针。 若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的 区域即为当前的窗口），经常用于区间搜索。

若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是 排好序的。

对于 C++ 语言，指针还可以玩出很多新的花样。

此类题型主要有

• 双指针（遍历方向相反）
• 快慢指针
• 滑动窗口

滑动窗口

76.最小覆盖子串（第二遍没做出来）

• 思想：我们在 s上滑动窗口，通过移动 r指针不断扩张窗口。当窗口包含 t所需的全部所需的字符后，如果能收缩且保证还继续满足条件，我们就收缩窗口直到得到最小窗口。直到不满足条件，就r继续向右移动。

680. 验证回文串 II(第二次写出来了)

3. 二分查找

682.搜索旋转排序数组

4. 排序

桶排序:
451. 根据字符出现频率排序

452. 颜色分类

5. 二叉树

前中后序非递归
102.二叉树的层序遍历
101. 对称二叉树
111. 二叉树的最小深度

5. dfs 和 bfs

695.岛屿的最大面积 :最基础的遍历题。（第二遍一次过）
547. 省份数量(第二遍，看答案过)
548. 太平洋大西洋水流问题

5.1 回溯

看代码随想录的回溯知识点。

回溯法模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

注意：做回溯的题，要画树，需要确定两个值（通过画树来判断）：

• 确定好for遍历的范围
• 遍历的深度，也就是确定终止条件
• 其他注意的点：
  • 一般组合、求子集、分割问题，for循环i从startIndex开始，递归的时候传入的是i+1
  • 排列问题，for循环i从0开始，不需要startIndex（排列可以重复）。但是需要一个used数组记录使用过的数

纵向递归，横向遍历：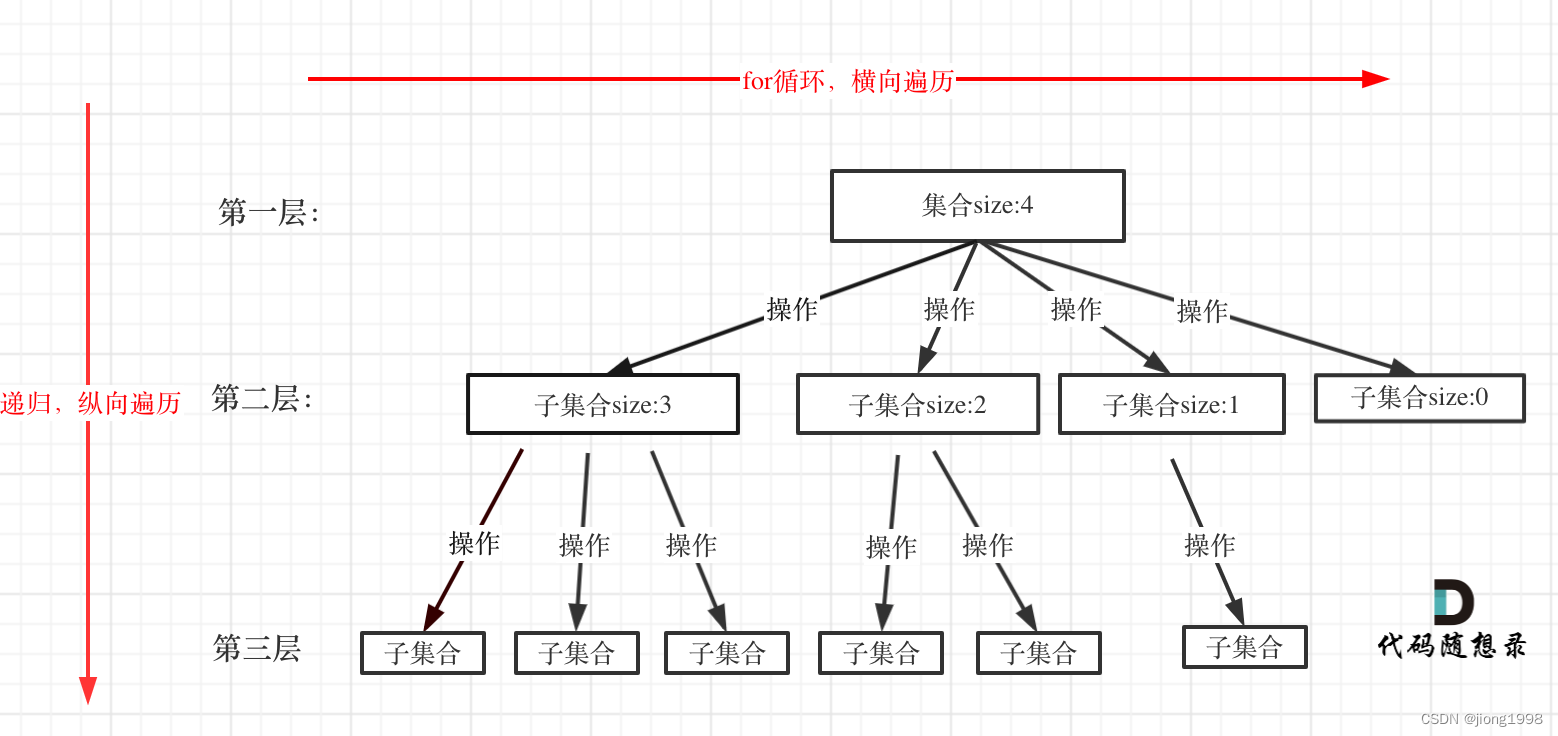

77.组合
216.组合总和III
40.组合总数II（先做39.组合总数，在做40）

• 难点：数字有重复，但是结果又要求不重复。（要理解：“树层去重”和“树枝去重”非常重要。）这种题一般要求的是树层去重
• 解决办法：要解决数字有重复，结果不重复，首先要求数组是排序的，在排序的基础上在for循环里，要首先判断if(nums[i]和nums[i-1])的关系。
• 注意：思考是否可以通过set来解决去重问题。（可以，利用set去重复，）
• 那如果是树枝去重呢？
• 解决办法：通过for循环的是i+1

131.分割回文串

• 大体上有思路，小细节问题（慢慢熟悉回溯了）

78.子集

• 难点：树不会画，参考了代码随想录才知道树要这么画。
• 解析：求子集和求组合的方式有点不一样，不一样的点在于：result.push_back(path)的位置。重复问题和组合问题一样，但是还可以通过set来解决（是否其他的重复问题都可以通过set解决？二刷的时候注意）。

491.递增子序列

• 难点：重复问题，该重复问题没办法用上面讲过的重复来解决。不能在同一个父节点下同时使用同一个数字，否则就会有重复问题
• 解决办法：利用set，每次在path.push_back()前，先看看之前是否用过

求子集2、递增子序列和、组合的去重 都是 同一父节点下本层的去重。

46.全排列
47.全排列2

• 排列的重复问题怎么解决
• 其实和组合的重复问题一样。具体自己的分析看最新的提交记录

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

51.N 皇后

• 难点：用回溯解决多了组合、切割、子集、排列问题之后，遇到这种二维矩阵还会有点不知所措，不知道怎么遍历
• 解决办法：维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。（棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度）

37.解数独

• 难点：二维矩阵，遍历的方式和N皇后又不太一样，N皇后一行只需要放一个值
• 解决办法：for循环用于找一个空位，不找第二个空位，找到一个空位后递归的往下试每个数字。例如：先for循环找到第三个元素为空，测试1-9，发现’3’和’5’都符合题目要求，就先递归当前位置是3，然后在下一层继续查找一个空位，在找合适的值插入。

6. 动态规划

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌 握了！

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

总结：一般的动态规划题（除去背包问题），dp[i]或者dp[i][j]表达都是在i点或者i、j点的状态，他们都是由上一个状态(可能由a状态，或者b状态转移到dp[i][j])转变而来的，只要搞清楚：1、dp[i]状态如何定义，2、状态是如何转变的，就能用动态规划解决了。

62.不同路径(第二轮过)

• 难点：二维db数组

343.整数拆分（第二轮，不会）

• 难点：递归公式不好推

96.不同的二叉搜索树

• 难点：递归公式不好推
• 得到经验：画图看规律，脑子是想不出来的！

213.打家劫舍 II

• 如何处理回环问题？

300.最长递增子序列

516.最长回文子序列

718.最长重复子数组

1143.最长公共子序列

392.判断子序列

115.不同的子序列

583.两个字符串的删除操作

背包问题

难点来了！

主要是01背包、完全背包。

• 01背包：商品只能用一次。
• 完全背包：商品可以多次使用

01背包问题

1. 二维dp数组数组解决01背包问题

五部曲来分析：
1 dp数组下标定义

• i代表从0-i的物品取
• j代表背包重量
• dp[i][j]代表当i、j时，价值最大总和。
  如下图所示：
  

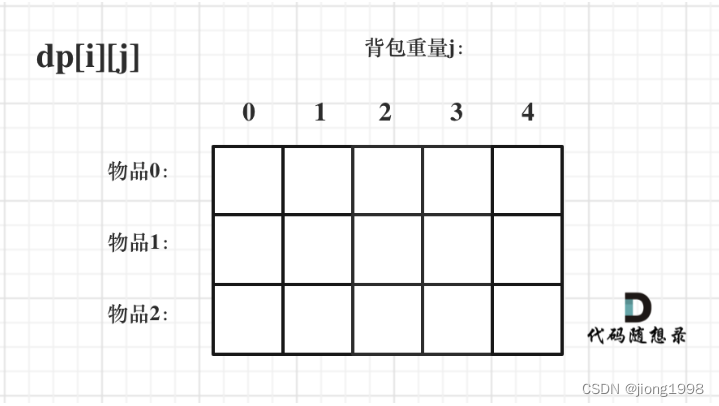
2 递推公式

dp[i][j] = max( dp[i-1][j], dp[i-1][ j-weight[j] ]+value[j] )
1

3 初始化

• 当重量为0时，即j=0，那么为0。dp[i][0] = 0
• 同时需要初始化i=0的情况（因为i由i-1推出来的），当i=0时，如果背包容量<weight[0]，则dp[0][j]=0。如果背包容量>=weight[0],则dp[0][j] = 第0个物品的价值

for(int i=0; i<weight.size(); ++i)
{
	dp[i][0] = 0;
}
for(int j=0; j<=bagweight; ++j)
{
	if(j<weight[0])
		dp[0][j] = 0;
	else
		dp[0][j] = value[0];
}
1
2
3
4
5
6
7
8
9
10
11

初始化完的dp数组如下所示：

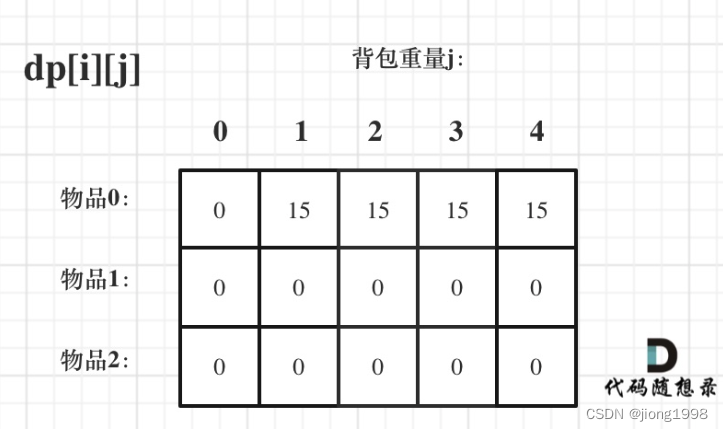
完整代码

int 01_bag(int bagweight, vector<int>weight, vector<int> value)
{
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight+1, 0));
    //初始化
    for(int j=weight[0]; j<=bagweight; ++j)
    {
        dp[0][j] = value[0];
    }
    //两个for循环，先遍历物品，在遍历包的重量
    for(int i=1; i<weight.size(); ++i)
    {
        for(int j=0; j<=bagweight; ++j)
        {
            if(j<weight[i])//如果当前包的大小不足以装下第i个商品
                dp[i][j] = dp[i-1][j];
            else
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
        }
    }
    return dp[weight.size()-1][bagweight];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

2. 一维数组解决01背包问题

将二维降为一维时：dp数组的构建只和背包重量有关。但是这不是说物品顺序i就没有关系，将会体现在for循环上。

1 dp数组下标定义

• j代表背包重量
• dp[j]代表当背包容量为j时，价值最大总和。

2 递推公式

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
1

3 初始化
和二维数组的方法一样，初始化为0就行

4 遍历顺序
这个是重点！！物品的遍历和二维数组一样，而重量的遍历要从大到小遍历！！原因看代码随想录知识点

for(int i = 0; i < weight.size(); i++) 
	{ 
	 // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--)
    	// j >= weight[i]是因为j是背包大小，当j小于当前物品的重量时，就没必要继续遍历了
    	{
    	 // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); 
    	}
	}
1
2
3
4
5
6
7
8
9
10

题目

416.分割等和子集

• 解析看我的提交答案的备注

1049.最后一块石头的重量 II

• 解析看我的提交答案的备注

总结：上面这两题其实是通过动态规划找到最大重量的题，需要把题目转换为找到最大数/最d大重量。

完全背包问题：

• 01背包：商品只能用一次。
• 完全背包：商品可以多次使用

7. 单调栈

什么时候考虑单调栈：
通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是只需要遍历一次。

739.每日温度
503.下一个更大元素 II
42.接雨水-（不用单调栈）

• 用双指针

---

系列2 剑指offer

1. 链表

JZ35 复杂链表的复制（第二遍做出来了）

• 暴力写出来了。有没有O(n)的方法？
• 提示：构建映射关系

2. 动态规划

JZ85 连续子数组的最大和(二)(第二遍没做出来)

3. 栈

JZ30 包含min函数的栈(第二遍没做出来)

• 难点：怎么使得求min也是o(1)

JZ59 滑动窗口的最大值（第二遍做出来了,但是时间复杂度是o(nlogn)）

• 提示：单调。

JZ71 跳台阶扩展问题

• 提示：推状态转移函数！

4. 算法

JZ53 数字在升序数组中出现的次数(第二遍没做出来)

• 难点：时间复杂度不满足要求

JZ11 旋转数组的最小数字

• 提示：就是找自旋点

JZ38 字符串的排列

• 回溯问题，如何去重复？

5. 回溯

JZ12 矩阵中的路径

• 不像回溯，像dfs
• 提示：把是否越界放在在dfs函数中判断会比较容易

6. 其他算法

JZ66 构建乘积数组(第二遍做出来了)

JZ39 数组中出现次数超过一半的数字(第二遍没做出来)

• 其实是会做的，不会空间O(1)，时间O(n)的算法，比较新颖。
• 候选人思想

JZ45 把数组排成最小的数

• 考虑使用lamuda表达式，不然太复杂

JZ49 丑数(第二遍没做出来)

• 提示：
• 怎么找到丑数？ 思考一下
• 小根堆+哈希存储去重复

JZ74 和为S的连续正数序列(第二遍看提示做出来了)

• 提示：
• 滑动窗口

JZ57 和为S的两个数字(第二遍做出来了)

• 提示：这题其实很简单
• 双指针

JZ75 字符流中第一个不重复的字符

• 傻了，很简单的

JZ14 剪绳子(第二遍看提示做出来了)

• 纯数学，想到就简单

双指针练习

977.有序数组的平方（使用On时间复杂度）(第二遍做出来了)
15. 三数之和(第二遍做出来了)

思路：先对数组按升序排序，排序的好处： 记第一个元素为nums[first], 当nums[first]>0时，则说明后面的元素都大于0，不可能形成a+b+c=0的情况，此时结束循环；相等的元素一定连续在一起，这样利于去重。 具体思路：先固定第一个元素的下标first, first的范围为[0,n-2], 然后需要寻找的目标就是-nums[first], 照nums[second]+nums[third]=target时，可以采用双指针法，left从前往后遍历，right从后往前遍历, 二者之和分为以下3种情况：
num[left]+nums[right]=target 找到 添加一个三元组到答案中 left++ right-- 同时进行去重操作
num[left]+nums[right]>target 此时right应该左移 使得整体变小
num[left]+nums[right]<target 此时left应该右移 使得整体变大

18.四数之和(第二遍没做出来了,建议在做一遍)

11.盛最多水的容器

986.区间列表的交集

• 对于两个区间，先获得两个区间左边界中的较大值，右边界中的较小值，如果这个较大值<=较小值，说明有交集

---

word 第二遍不熟悉的题

454.四数相加 II（第二遍想不到思路）
239. 滑动窗口最大值

• 提示：堆

240.简化路径
-提示：栈

代码随想录—额外题目

1365.有多少小于当前数字的数字(第三次只会暴力)
189. 轮转数组（第三遍没写出来）
143.重排链表（第三遍没写出来）
190. 岛屿的周长（第三遍写出来）
191. 机器人能否返回原点（第三遍写出来）

股票问题

121.买卖股票的最佳时机（第三遍没写出来）
122.最佳买卖股票时机含冷冻期（第三遍没写出来）

leetcode150热点题目

跳跃游戏 II（第三遍写出来）

O(1) 时间插入、删除和获取随机元素（第三遍没写出来）
加油站(写出来了，但是时间复杂度超了)
整数转罗马数字(不难，但是要想到那种方法)（第三遍没写出来）
字母异位词分组(思路没想到 )（第三遍没写出来）
最长连续序列（第三遍没写出来）
单词拆分（第三遍没写出来）
零钱兑换
寻找峰值
搜索旋转排序数组
寻找旋转排序数组中的最小值
旋转图像
数组中的第K个最大元素

• 堆的方法做一遍
• 快速排序的方法做一遍

三角形最小路径和
最长回文子串
最大正方形(找到dp的意义就会了)
交错字符串
距离相等的条形码

树

对称二叉树
二叉树的最小深度
完全二叉树的节点个数
平衡二叉树
二叉树的所有路径

• 请考虑回溯

左叶子之和