2024年最新密码学基础三-RSA非对称密码实验(1)，看懂这些帮你轻松解决就业问题年薪50万不是梦_在线非对称加密实验

本人从事网路安全工作12年，曾在2个大厂工作过，安全服务、售后服务、售前、攻防比赛、安全讲师、销售经理等职位都做过，对这个行业了解比较全面。

最近遍览了各种网络安全类的文章，内容参差不齐，其中不伐有大佬倾力教学，也有各种不良机构浑水摸鱼，在收到几条私信，发现大家对一套完整的系统的网络安全从学习路线到学习资料，甚至是工具有着不小的需求。

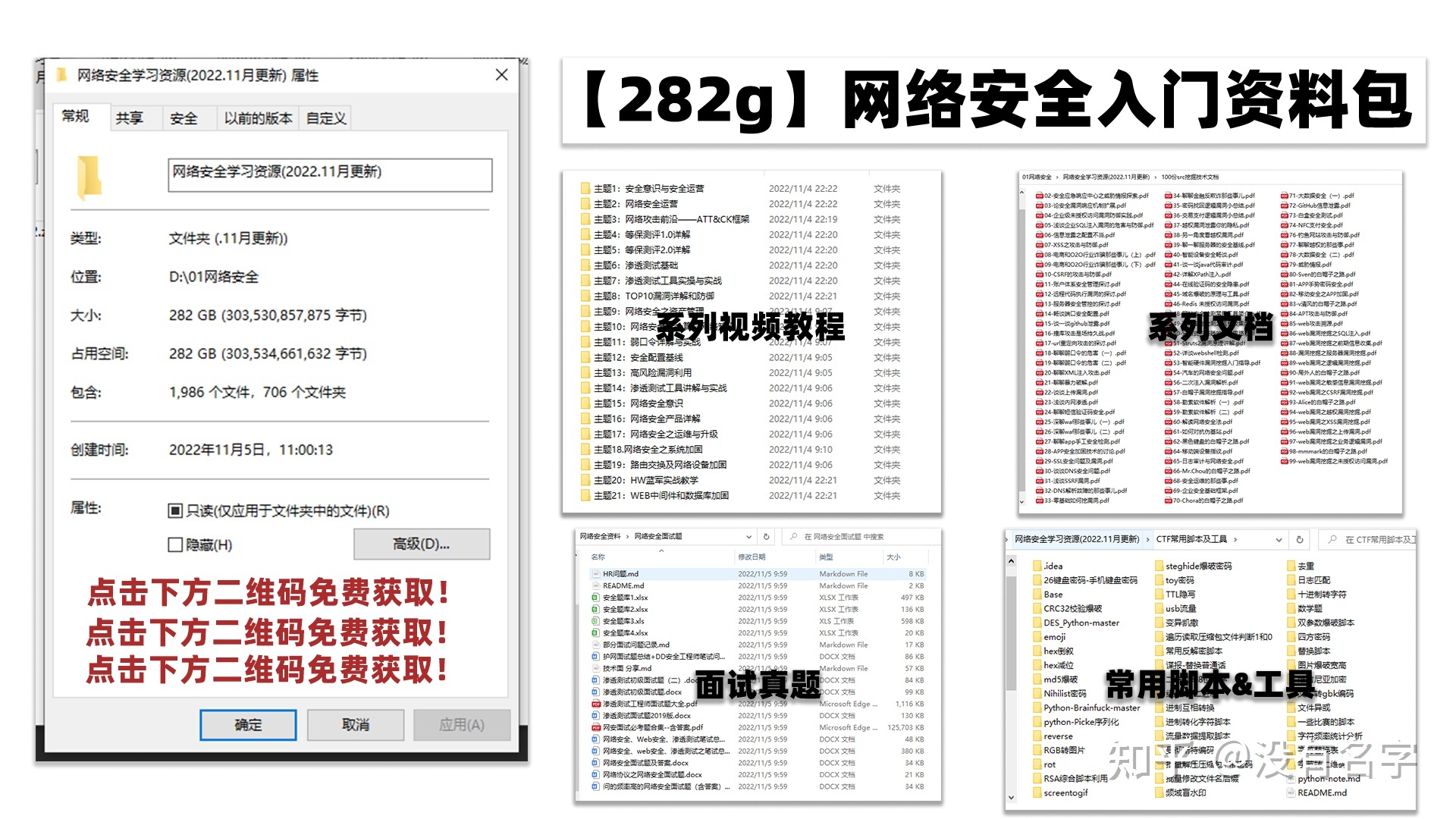
最后，我将这部分内容融会贯通成了一套282G的网络安全资料包，所有类目条理清晰，知识点层层递进，需要的小伙伴可以点击下方小卡片领取哦！下面就开始进入正题，如何从一个萌新一步一步进入网络安全行业。

学习路线图

其中最为瞩目也是最为基础的就是网络安全学习路线图，这里我给大家分享一份打磨了3个月，已经更新到4.0版本的网络安全学习路线图。

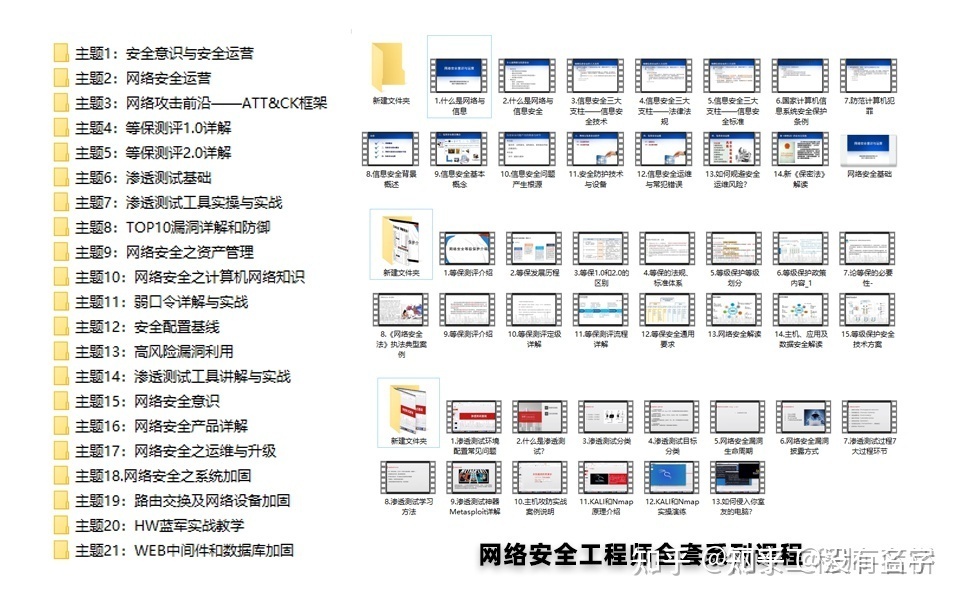
相比起繁琐的文字，还是生动的视频教程更加适合零基础的同学们学习，这里也是整理了一份与上述学习路线一一对应的网络安全视频教程。

网络安全工具箱

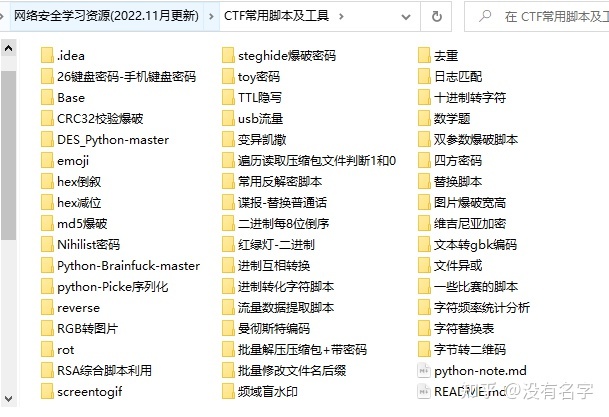
当然，当你入门之后，仅仅是视频教程已经不能满足你的需求了，你肯定需要学习各种工具的使用以及大量的实战项目，这里也分享一份我自己整理的网络安全入门工具以及使用教程和实战。

项目实战

最后就是项目实战，这里带来的是SRC资料&HW资料，毕竟实战是检验真理的唯一标准嘛~

面试题

归根结底，我们的最终目的都是为了就业，所以这份结合了多位朋友的亲身经验打磨的面试题合集你绝对不能错过！

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以点击这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

而非对称加密算法需要两个密钥来进行加密和解密，

这两个秘钥是公开密钥（public key，简称公钥）和私有密钥（private key，简称私钥）。

非对称加密与对称加密相比，其安全性更好：对称加密的通信双方使用相同的秘钥，如果一方的秘钥遭泄露，那么整个通信就会被破解。而非对称加密使用一对秘钥，一个用来加密，一个用来解密，而且公钥是公开的，秘钥是自己保存的，不需要像对称加密那样在通信之前要先同步秘钥。

非对称加密的缺点是加密和解密花费时间长、速度慢，只适合对少量数据进行加密。

【非对称加密算法】：

公开密钥与私有密钥是一对。

如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；

如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥。

II、了解RSA的概念。

【RSA加密算法】：

是一种非对称加密算法。

对极大整数做因数分解的难度决定了RSA算法的可靠性。

换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。

III、了解RSA算法。

非对称算法的在应用的过程如下，假设发送方向接收方发送消息（明文）：

1、接收方生成公钥和私钥，公钥公开，私钥保留；

2、发送方将要发送的消息采用公钥加密，得到密文，然后将密文发送给接收方；

3、接收方收到密文后，用自己的私钥进行解密，获得明文。

可以看出，非对称加密解决了对称加密密钥传输的问题。

-数学基础

–互质关系

1、素数

素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。

2、互质数

公因数只有1的两个数，叫做互质数；又称互素，若N个整数的最大公因子是1，则称这N个整数互质。

判断互质的简单法则：

a.任意两个质数是互质的；

b.一个数是质数，另一个数不是它的倍数，两者互质（比如正整数P是质数，则小于P的正整数和P都是互质的）；

c.两个不相等的数，较大的那个数是质数，两者互质；

d.1和任意自然数互质；

e.2和任何奇数是互质；

f.如果P是大于1的整数，则P和P-1互质；

g.如果P是大于1的奇数，则P和P-2互质。

–欧拉函数

欧拉函数的意义在于计算在小于等于任意正整数n的正整数中，有多少个与n互质的正整数。
是小于n并与n互质的正整数的个数。是质数。

–欧拉定理

如果两个正整数a和n互质，则n的欧拉函数

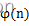
可使下面等式成立：

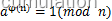
上式表示，a的次方被n除的余数为1，或者叙述为，a的 次方减去1后可以被n整除。

注意，是n的欧拉函数。

欧拉定理的特殊情况：如果正整数a与质数p互质，因为质数p的等于p-1，则欧拉定理可以写成就是我们所说的费马小定理。

–模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1。这时b被称为a的模反元素。公式如下：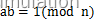

–扩展欧几里得算法

欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：

gcd函数就是用来求(a,b)的最大公约数的。

gcd函数的基本性质：

gcd(a,b)=gcd(b,a)=gcd(-a,b)=gcd(|a|,|b|)

对于不完全为 0 的非负整数 a，b，gcd(a,b)表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd(a,b)=ax+by。

先自我介绍一下，小编浙江大学毕业，去过华为、字节跳动等大厂，目前阿里P7

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年最新网络安全全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上网络安全知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化资料的朋友，可以点击这里获取

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上网络安全知识点，真正体系化！*

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化资料的朋友，可以点击这里获取