【机器学习 复习】第7章 集成学习（小重点，混之前章节出题但小题）

一、概念

1.集成学习，顾名思义，不是一个玩意，而是一堆玩意混合到一块。

（1）基本思想是先 生成一定数量基学习器，再采用集成策略 将这堆基学习器的预测结果组合起来，从而形成最终结论。

（2）一般而言，基学习器可以是同质的“弱学习器”，也可以是异质的“弱学习器”。 （3）目前，同质基学习器应用最广泛，其使用最多的模型是CART决策树和神经网络。

2.生成基学习器

同质个体学习器按照个体学习器之间是否存在依赖关系又可以分为两类：

（1）存在着强依赖关系，串行生成个体学习器。

原理是利用依赖关系，对之前训练中错误标记的样本赋以较高的权重值，以提高整体的预测效果。

代表算法是Boosting算法。

（2）不存在强依赖关系，并行生成这些个体学习器。

并行的原理是利用基学习器之间的独立性，通过平均可以显著降低错误率。

代表算法是Bagging和随机森林（Random Forest）算法。

3.集成策略

根据集成学习的用途不同，结论合成的方法也各不相同。

（1）通常是由各个体学习器的输出投票产生。

通常采用绝对多数投票法或相对多数投票法。

（2）当用于回归估计时，一般由各学习器的输出通过 简单平均或加权平均产生。

4.Bagging

（1）思路是从原始样本集合中采样，得到若干个大小相同的样本集，然后在每个样本集合上分别训练一个模型，最后用投票法进行预测。

（2）采样方式：用于训练的每个模型的样本集合Dt是从D中有放回采样得到的

（3）训练得到的模型可用于分类也可用于回归:

    分类：投票法

    回归：加权平均法

5.随机森林

说白了就是建了一堆简单版的决策树，然后放一块变成森林模拟器，这个健壮性一下就上来了。

（1）抽样产生每棵决策树的训练数据集。

随机森林从原始训练数据集中产生n个训练子集（假设要随机生成n棵决策树）。

训练子集中的样本存在一定的重复，主要是为了在训练模型时，每一棵树的输入样本都不是全部的样本，使森林中的决策树不至于产生局部最优解。

（2）构建n棵决策树（基学习器）。

每棵决策树不需要剪枝处理。由于随机森林在进行结点分裂时，随机地选择m个特征参与比较，而不是像决策树将所有特征都参与特征指标的计算。这样减少了决策树之间的相关性，提升了决策树的分类精度，从而达到结点的随机性。

（3）生成随机森林。使用第（2）步n棵决策树对测试样本进行分类，随机森林将每棵子树的结果汇总，以少数服从多数的原则决定该样本的类别。

    

6. Boosting

（1）是一种可将弱学习器提升为强学习器的算法。

这种算法先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器。

（2）如此重复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权结合。

（3）分好几种，如AdaBoost，GradientBoosting，LogitBoost等，其中最著名的代表是AdaBoost算法。Boosting中的个体分类器可以是不同类的分类器。

7.偏差与方差（重点）

（1）偏差bias

偏差是指预测结果与真实值之间的差异，排除噪声的影响，偏差更多的是针对某个模型输出的样本误差。

偏差是模型无法准确表达数据关系导致，比如模型过于简单，非线性的数据关系采用线性模型建模，偏差较大的模型是错的模型。

（2）方差variance

模型方差不是针对某一个模型输出样本进行判定，而是指多个(次)模型输出的结果之间的离散差异（注意这里写的是多个(次)模型，即 不同模型 或 同一模型不同时间 的输出结果方差较大）。

方差是由训练集的数据不够导致。

一方面量 (数据量) 不够，有限的数据集过度训练导致模型复杂，另一方面质(样本质量)不行，测试集中的数据分布未在训练集中，导致每次抽样训练模型时，每次模型参数不同，导致无法准确的预测出正确结果。

（3）偏差决定中心点（期望输出与真实标记的差别），方差决定分布（使用样本数相同的不同训练集产生的方差）：

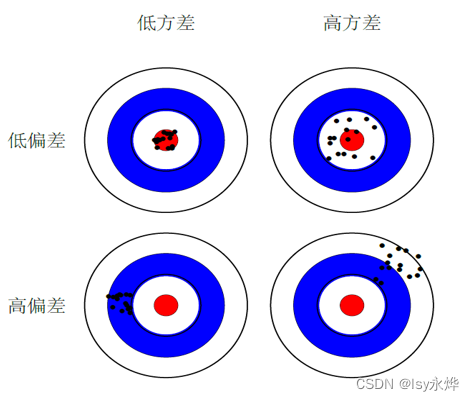
（4）泛化误差可以分解为偏差（Biase）、方差（Variance）和噪声（Noise）

8.如何解决偏差、方差问题

首先，要知道偏差和方差是无法完全避免的，只能尽量减少其影响。

（1）偏差：实际上也可以称为避免欠拟合。

             1.寻找更好的特征 -- 具有代表性。

             2.更多的特征 -- 增大输入向量的维度，增加模型复杂度。

（2）方差：实际上也可以称为避免过拟合 。

             1.增大数据集合 -- 使用更多的数据，减少数据扰动所造成的影响

             2.减少数据特征 -- 减少数据维度，减少模型复杂度

             3.正则化方法

             4.交叉验证法

二、习题

单选题

11. 集成学习的主要思想是（B）。

A、将多源数据进行融合学习  

B、将多个机器学习模型组合起来解决问题  

C、将多个数据集合集成在一起进行训练  

D、通过聚类算法使数据集分为多个簇  

12. 下列不是Bagging算法特点的是（D）。

A、各基分类器不存在强依赖关系，并行生成基分类器  

B、各基分类器权重相同，训练出来的每个模型独立同分布  

C、通过有放回采样获取每个模型的样本集合  

D、只需要较少的基分类器  

Bagging算法通常会生成多个基分类器，而不是较少的。增加基分类器的数量可以提高整体模型的泛化能力和稳定性。

13. 下列关于随机森林的说法错误的是（B）。

A、易于实现、易于并行。  

B、基本单元是决策树，将所有特征都参与特征指标的计算。  

C、通过集成学习的思想将多棵树集成的一种算法。  

D、在引入样本扰动的基础上，又引入了属性扰动。  

在随机森林中，并不是所有特征都会参与到每棵树的建立中。随机森林在每棵树的建立过程中会随机选择一部分特征进行训练，这个过程被称为特征子集采样。

14. 下列哪个集成学习器的个体学习器存在强依赖关系（A）

A、Boosting  

B、Bagging  

C、EM  

D、Random Forest  

15. 下列哪个不是Boosting 的特点（D）

A、基分类器彼此关联  

B、串行训练算法  

C、通过不断减小分类器的训练偏差将弱学习器提升为强学习器  

D、Boosting中的基分类器只能是不同类的分类器  

16. 模型的方差（B），说明模型在不同采样分布下，泛化能力大致相当；

模型的偏差（），说明模型对样本的预测越准，模型的拟合性越好。

A、越小    越大  

B、越小    越小  

C、越大    越小  

D、越大    越大  

17. 在集成学习两大类策略中，boosting和bagging如何影响模型的偏差（bias）和方差（variance）（ C  ）。

A、boosting和bagging均使得方差减小  

B、boosting和bagging均使得偏差减小  

C、boosting使得偏差减小，bagging使得方差减小  

D、boosting使得方差减小，bagging使得偏差减小  

boosting是打一个样本集不断优化的战斗对应偏差是样本偏差，bagging是玩一堆方法去养蛊对应方差针对“多”这个特点。

判断题

14. 低方差的优化结果比高方差的优化结果更集中（ P）

15. 模型的方差和偏差之和越大，模型性能的误差越小，泛化能力越强（Í ）

不论是偏差还是方差都是越小越好