- 1Tkinter10_布局管理器_tkinter三个坐标管理器
- 2Python3 * 和 ** 运算符
- 3用Python实现语音播报_语音播报python
- 4微信小程序radio不能改变大小?那我自己写一个吧_小程序 radiogroup 圆圈大小
- 5怎么解决网站“不安全”提醒?_网站提示没有证书不安全
- 6前端三大主流框架中文文档_web前端三大主流框架
- 7nacos配置使用教程
- 8Oracle数据库存储过程---在存储过程中返回结果集
- 9【计算机毕业设计】264民族婚纱预定系统_婚纱系统摘要
- 10【python】电影评分数据集的分析(python实现)(源码+报告)【独一无二】_要求用python完成,针对电影数据集给出推荐列表实验报告
机器学习-鸢尾花(Iris Flower)分类_鸢尾花 机器学习
赞
踩

鸢尾花分类是机器学习的经典案例了,在这里我们将使用鸢尾花数据集——一个非常容易理解的数据集(花瓣和花萼的长度与宽度),对鸢尾花的3个亚属:山鸢尾(Iris-setosa)、变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)进行分类。
接下来我们将通过如下步骤实现这个项目,以展示一个机器学习项目的所有步骤。
- 导入数据
- 概述数据
- 数据可视化
- 评估算法
- 实施预测
1、导入数据
导入项目中所需要的类库和方法,代码如下:
"""导入类库和方法""" from pandas import read_csv from pandas.plotting import scatter_matrix from matplotlib import pyplot from sklearn.model_selection import train_test_split from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score from sklearn.linear_model import LogisticRegression from sklearn.tree import DecisionTreeClassifier from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.neighbors import KNeighborsClassifier from sklearn.naive_bayes import GaussianNB from sklearn.svm import SVC
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
导入数据集:
在UCI机器学习仓库下载鸢尾花数据集,完成后保存在项目地址下。我们将使用Pandas来导入数据并且对数据集进行描述性统计与分析。
导入数据的同时设定数据的名称
| separ-length | separ-width | petal-length | petal-width | class |
|---|---|---|---|---|
| 萼片长度 | 萼片宽度 | 花瓣长度 | 花瓣宽度 | 类别 |
代码如下:
"""导入数据"""
filename = 'iris.data.csv'
names = ['separ-length', 'separ-width', 'petal-length', 'petal-width', 'class']
dataset = read_csv(filename, names=names)
- 1
- 2
- 3
- 4
2、概述数据
得到数据后,我们查看需要具体查看数据的维度、内容、特征、分布情况等等。代码如下:
"""提要输出"""
# 显示数据的维度:
print("行:%s , 列:%s" % dataset.shape)
# 查看数据前10行:
print(dataset.head(10))
# 数据的统计信息:
print(dataset.describe())
#数据的分布情况:
print(dataset.groupby("class").size())
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
每个亚属的数据各有50条,分布均衡。如果数据分布不均衡,我们通常会尝试扩大数据样本、重新抽样、人工生成样本、数据异常排除等方案来解决这样的问题。
3、数据可视化
通过数据的审查后,对其基本情况以有了解,接下来将使用图表来进一步分析数据。
首先对单变量进行分析,采取箱线图和直方图来进行分析,
箱线图:描述属性与中位值的离散速度。
直方图:显示每个特征的分布状态。
代码如下:
"""单变量图表"""
#箱线图
dataset.plot(kind="box", subplots=True, layout=(2, 2), sharex=False, sharey=False)
#直方图
dataset.hist()
"""显示图片"""
pyplot.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
我们将得到如下两张图表:
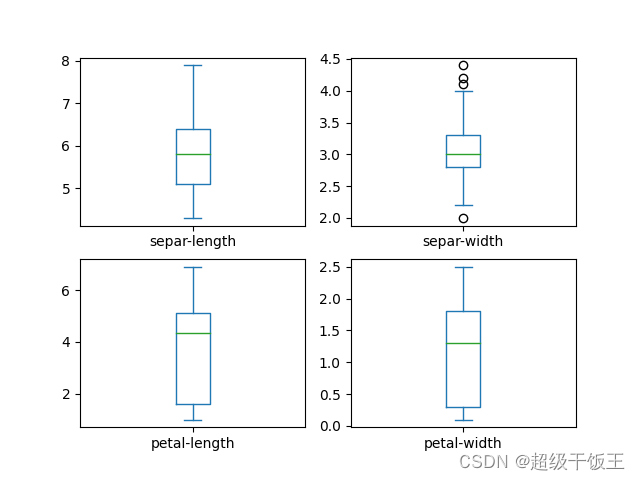 | 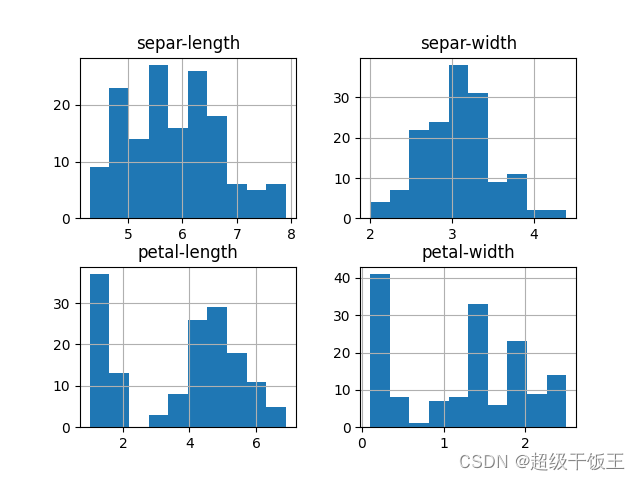 |
|---|
接下来,我们通过散点矩阵图来查看不同属性之间的关系:
"""多变量图表"""
#散点矩阵图
scatter_matrix(dataset)
"""显示图片"""
pyplot.show()
- 1
- 2
- 3
- 4
- 5
得到如下图表:
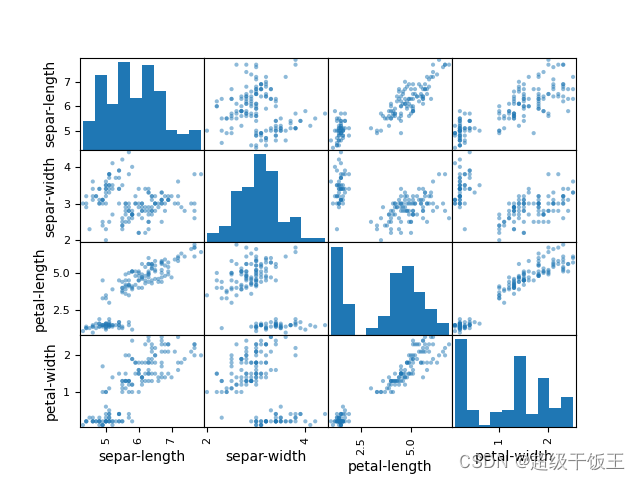
4、评估算法
根据不同的算法来创建模型,并且评估他们的准确度,以便找到最合适的算法。
分离出评估的数据集。
要验证通过算法创建的模型是否合格,比较出更加优秀的模型,我们得从数据集中分离出一部分,用于评估模型的准确度。
以下,我们按照2 8分分离训练数据集与测试数据集,及:80%的数据用于训练,20%的数据用于评估测试:
"""分离数据 分离评估数据集"""
array = dataset.values
X = array[:, 0:4]
Y = array[:, 4]
validation_size = 0.2
seed = 7
X_train, X_validation, Y_train, Y_validation = \
train_test_split(X, Y, train_size=validation_size, random_state=seed)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
如上,我们分离出了X_train和Y_train用来训练算法创建模型,X_validation与Y_validation用于验证评估模型。
创建模型
我们不能仅仅通过对数据的审查来判断那种算法最有效。我们将尝试评估以下六种算法:
- 线性回归(Linear Regression,LR)
- 线性判别分析 (linear Discriminant Analysis,LDA)
- K最近邻 (k-Nearest Neighbor,KNN)
- 分类与回归树 (Classification And Regression Tree)
- 朴素贝叶斯(Naïve Bayes,NB)
- 支持向量机(Support Vector Machine, SVM)
为保证算法评估的准确性,我们在每次算法评估之前重新设置随机种子数,使得每次算法评估的过程中都使用的是相同的数据集。
"""算法审查"""
models = {}
models["LR"] = LogisticRegression(max_iter=1000)
models["LDA"] = LinearDiscriminantAnalysis()
models["KNN"] = KNeighborsClassifier()
models["CART"] = DecisionTreeClassifier()
models["NB"] = GaussianNB()
models["SVM"] = SVC()
"""评估算法"""
results = []
for key in models:
kfold = KFold(n_splits=10, random_state=seed, shuffle=True)
cv_results = cross_val_score(models[key], X_train, Y_train, cv=kfold, scoring="accuracy")
results.append(cv_results)
print("%s:%f(%f)" %(key, cv_results.mean(), cv_results.std()))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
选择最优模型
执行上述代码,我们得到对于各种算法的准确度得分:
LR:0.866667(0.163299)
LDA:0.933333(0.133333)
KNN:0.900000(0.213437)
CART:0.933333(0.133333)
NB:0.900000(0.152753)
SVM:0.900000(0.152753)
在以上的评分中,LDA与CART获得较高的评分。同样,我们也将评分结果用箱线图显示出来:
"""箱线图比较算法"""
fig = pyplot.figure()
fig.suptitle("Algorithm Comparison")
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(models.keys())
pyplot.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
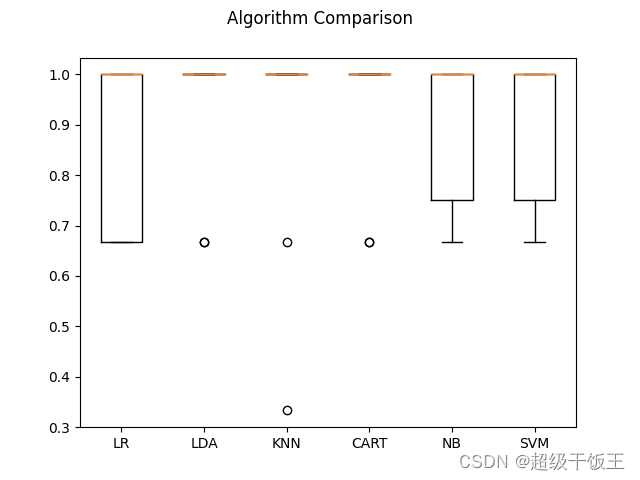
5、实施预测
现在我们选取线性判别分析 (LDA)算法,使用预留的评估数据集来验证这个算法模型,这将能更加准确的了解模型的准确度情况。
以下,使用全部训练数据集的数据来生成LDA算法的模型,并且用预留的评估数据集进行测试,再生成算法模型报告:
"""使用评估数据集评估算法模型"""
svm = LinearDiscriminantAnalysis()
svm.fit(X=X_train,y=Y_train)
predictions = svm.predict(X_validation)
print(accuracy_score(Y_validation, predictions))
print(confusion_matrix(Y_validation,predictions))
print(classification_report(Y_validation,predictions))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
执行以上程序,得到报告如下:
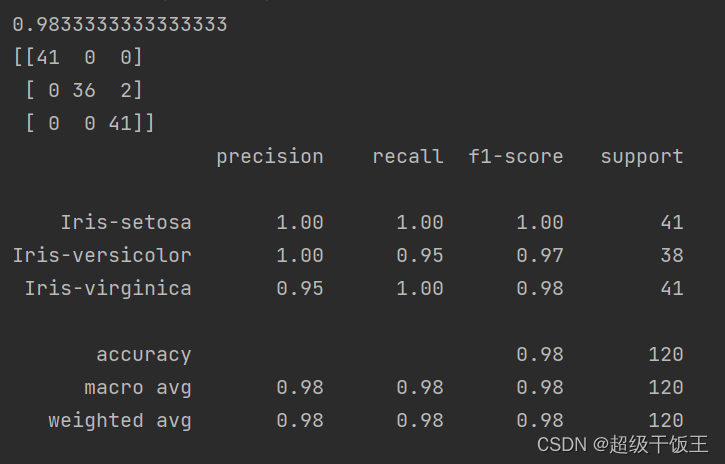
可以看到该算法模型的准确度达到0.98,我们还得到了冲突矩阵、精确度(precision) 、召回率(recall)、F1值(f1-score)等数据。
总结
至此,我们已经完成了一个非常简单的机器学习项目。该项目包括:导入数据,概述数据,数据可视化,评估算法,实施预测的全部过程。我们也将继续探索机器学习领域,尝试实践对数据进行处理和分析的算法与技巧以及算法的改进。



