信号链噪声分析14_量化噪声为啥分布在奈奎斯特频率内

概要

提示：这里可以添加技术概要

    虽然噪声的均方根值可通过 q/√12 计算精确近似值，但在某些条件下，频域成分可能 与交流输入信号高度相关。例如，低幅度周期性信号的相关度大于高幅度随机信号的 相关度。通常假设理论量化噪声表现为白噪声，均匀地分布在 DC 至 fs/2 的奈奎斯特 带宽范围。但是，事实并非全然如此。在强相关的情况下，量化噪声集中在输入信号 的各次谐波上，这正是我们不希望看到的。

整体架构流程

提示：这里可以添加技术整体架构

     在多数实际应用中，ADC 的输入是一段频率（总是会与一些不可避免的系统噪声相加）， 因此量化噪声往往是随机的。然而，在频谱分析应用中（或者使用频谱纯净的正弦波 作为输入对 ADC 执行 FFT），量化噪声与信号的相关度取决于采样频率与输入信号的 比值

技术名词解释

提示：这里可以添加技术名词解释

ADC:
      模拟数字转换器即A/D转换器，或简称ADC，通常是指一个将模拟信号转变为数字信号的电子元件。通常的模数转换器是将一个输入电压信号转换为一个输出的数字信号。由于数字信号本身不具有实际意义，仅仅表示一个相对大小。故任何一个模数转换器都需要一个参考模拟量作为转换的标准，比较常见的参考标准为最大的可转换信号大小。而输出的数字量则表示输入信号相对于参考信号的大小

技术细节

提示：这里可以添加技术细节

      注意，从 ADC 看到的谐波失真的这种变化是采样过程的伪像，由量化误差与输入频率 的相关性引起。在实际 ADC 应用中，量化误差一般表现为随机噪声，原因是宽带输入 信号具有随机性，而且通常会有少量的系统噪声充当“扰动”信号，使量化误差频谱 进一步随机化。 理解上述原理非常重要，因为 ADC 的单音正弦波 FFT 测试是公认的性能评估方法之 一。为了精确测量 ADC 的谐波失真，必须采取措施确保测试设置能够真正测量 ADC 失真，而不是量化噪声相关性引起的伪像。因此，必须正确选择频率比，有时还要将 少量噪声（扰动）与输入信号相加。利用模拟频谱分析仪测量 DAC 失真时，也应采取 同样的防范措施。 

        显示了一个理想 12 位 ADC 的 FFT 输出。注意，FFT 噪底的平均值约为满量程以 下 107dB，但 12 位 ADC 的理论 SNR 为 74dB。FFT 噪底并非 ADC 的 SNR，因为 FFT 像是一个带宽为 fs/M 的模拟频谱分析仪，其中 M 为 FFT 中的点数。由于 FFT 的处理 增益，理论 FFT 噪底因而比量化噪底低 10log10(M/2)dB

      对于 SNR 为 74dB 的理想 12 位 ADC，4096 点 FFT 将产生 10log10(4096/2)=33dB 的处 理增益，因此总 FFT 噪底为 74+33=107dBc。事实上，FFT 噪底可以通过提高 FFT 点 数来进一步降低，就像模拟频谱分析仪的噪底可以通过缩小带宽来降低一样。因此， 利用 FFT 测试 ADC 时，必须确保 FFT 足够大，使得失真能够与 FFT 噪底本身区别开。 多次 FFT 的平均值无法进一步降低噪底，只能减小各个噪声谱成分幅度之间的差异。

小结

提示：这里可以添加总结

例如：

本文描述了推导过程的三个不同阶段： 

1. 理想的模数转换器(ADC)传递函数公式和操作。

2. 基于积分法的均方根(rms)推导。‘

3. SNR 公式推导，以获得 SNR=6.02N+1.76dB 值。’

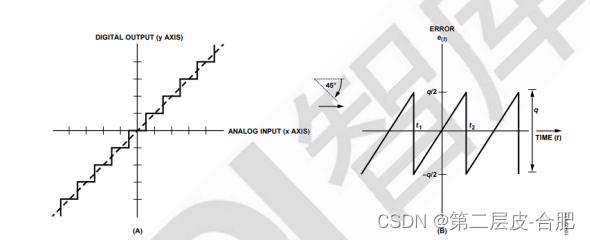
理想的 ADC 传递函数。数字（二进制）输出值表示为 y 轴，模拟输入则 表示为 x 轴。对角线阶梯表示模拟输入信号的量化值。穿过阶梯的虚线表示其中点。 表示采用斜坡输入信号时理想 N 位 ADC 的量化噪声。1LSB 峰峰值量化误差可 以通过一个最大峰峰值摆幅为 q（范围为 q/2 至–q/2）的非相关锯齿波形来近似计算。 请注意，t1 和 t2 为时间点，将用在稍后的推导阶段。该信号为量化输出信号（实线） 与模拟输入信号（虚线）之差。