【Python数据插值】_插值python

1. 数据插值

---

插值是一种从离散数据点构建函数的数学方法。插值函数或者插值方法应该与给定的数据点完全一致。插值可能的应用场景：

1. 根据给定的数据集绘制平滑的曲线
2. 对计算量很大的复杂函数进行近似求值

插值和前面介绍过的最小二乘拟合有些类似。在最小二乘拟合中，我们感兴趣的是使用数据点和超定方程组，将函数拟合到数组点，使得误差平方和最小。在插值中，我们需要一个方程能够与已有的数据点完全重合，仅使用与插值函数自由参数个数相同的数据点。因此，最小二乘法适合将大量数据点拟合到模型函数，插值是根据少量数据点创建函数。

外插（extrapolation）是与插值（interpolation）相关的一个概念。外插是在采样范围之外计算函数的估计值。我们这里只介绍插值。

2. 导入模块

---

本部分我们将使用NumPy中的polynomial模块和SciPy的interpolation模块。

import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt

from numpy import polynomial as P
from scipy import interpolate
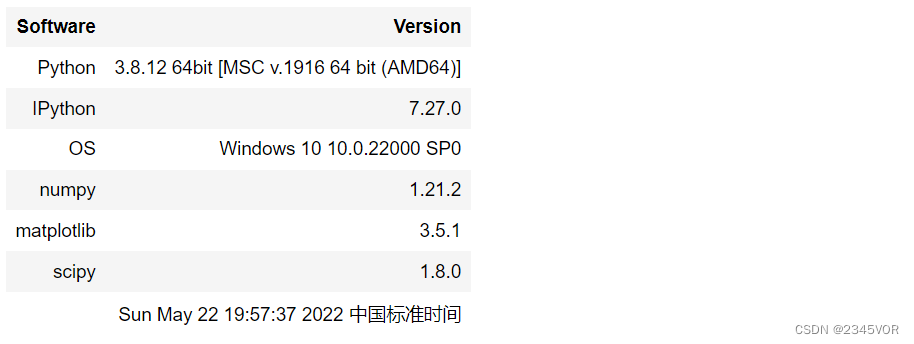
%reload_ext version_information
%version_information numpy, matplotlib, scipy
1
2
3
4
5
6
7
8

3. 插值函数

---

为了简洁起见，我们这里只考虑一维插值问题。对于给定的数据点的集合 { ( x i , y i ) } i = 1 n \left\{ (x_i, y_i) \right \}_{i=1}^n {(xi​,yi​)}i=1n​，找到插值函数$f(x_i)=y_i$。插值函数的选择并不是唯一的，事实上有无数函数满足插值标准。通常可以把插值函数写为一组基函数$\varphi (x)$的线性组合，即$f(x)=\sum _{j=1}^n{c}_j{\varphi }_j(x)$，其中$c_j$是未知系数。将给定的数据点代入线性组合，可以得到未知系数的线性方程组：

[ ϕ 1 ( x 1 ) ϕ 2 ( x 1 ) ⋯ ϕ n ( x 1 ) ϕ 1 ( x 2 ) ϕ 2 ( x 2 ) ⋯ ϕ n ( x 2 ) ⋮ ⋮ ⋱ ⋮ ϕ 1 ( x n ) ϕ 2 ( x n ) ⋯ ϕ n ( x n ) ] [ c 1 c 2 ⋮ c n ] [ y 1 y 2 ⋮ y n ]

$$\begin{bmatrix} \phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_n(x_1) \\ \phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_n(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1(x_n) & \phi_2(x_n) & \cdots & \phi_n(x_n) \end{bmatrix}$$ $$\begin{bmatrix}c_1 \\ c_2 \\ \vdots \\ c_n\end{bmatrix}$$ $$\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}$$ ⎣⎢⎢⎢⎡​ϕ1​(x1​)ϕ1​(x2​)⋮ϕ1​(xn​)​ϕ2​(x1​)ϕ2​(x2​)⋮ϕ2​(xn​)​⋯⋯⋱⋯​ϕn​(x1​)ϕn​(x2​)⋮ϕn​(xn​)​⎦⎥⎥⎥⎤​⎣⎢⎢⎢⎡​c1​c2​⋮cn​​⎦⎥⎥⎥⎤​⎣⎢⎢⎢⎡​y1​y2​⋮yn​​⎦⎥⎥⎥⎤​

这里基函数的数量与数据点的数量想用，可以使用求解方程组的标准方法得到系数向$c$的唯一解。如果基函数的数量小于数据点的数量，该方程组是超定的，可能需要使用最小二乘拟合进行近似插值。

3.1 多项式

---

NumPy库包含的polynominal模块提供了处理多项式的函数和类。要创建Polynominal类的实例，可以将系数数组传给该类的构造函数。

p1 = P.Polynomial([1,2,3])
p1
1
2

也可以使用Polynomial.fromroots方法，通过指定多项式的根来初始化多项式。

p2 = P.Polynomial.fromroots([-1, 1])
p2
1
2

我们可以通过实例的方法访问其特性：

p1.roots() # 根
1

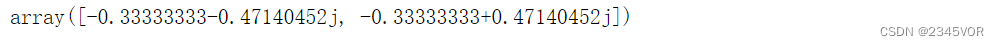
p1.coef # 系数

Polynomial实例包括domain和windows两个参数，可以用于把多项式的输入域映射到另外一个区间。

p1.domain
1

p1.window
1

多项式在用Polynomial实例表示后可以很容易计算任何$x$的多项式值。

p1(np.array([1.5, 2.5, 3.5]))
1

Polynomial实例支持标准的算术运算符。

p1 + p2
1

分解因式

p3 = P.Polynomial([1,1])  # 等价于 P.Polynomial.fromroots(-1)
p2 // p3
1
2

P.Polynomial.fromroots(-1)
1

除了标准幂基多项式的Polynomial类，polynomial模块还提供了切比雪夫多项式、勒让德多项式、拉盖尔多项式、埃尔米特多项式的类。

l1 = P.Legendre([1,2,3])  # 勒让德多项式
l1
1
2

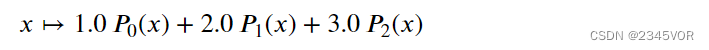
l1.roots()
1

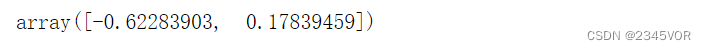
3.2 多项式插值

---

求解多项式插值问题，首先需要根据提供的基函数计算矩阵$\varphi (x)$，然后求解得到的线性方程组。polynomial模块中的每个多项式类都提供了方便的函数来计算相应基的范德蒙矩阵。

例如，假设存在数据点(1, 1)、(2, 3)、(3, 5)、(4, 4)。

x = np.array([1, 2, 3, 4])
y = np.array([1, 3, 5, 4])
deg = len(x) - 1
A = P.polynomial.polyvander(x, deg)  # 范德蒙矩阵
A
1
2
3
4
5

c = linalg.solve(A, y)
c
1
2

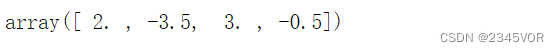
找到的插值多项式是$f(x)=2-3.5x+3x^2-0.5x^3$。

f1 = P.Polynomial(c)
f1(2.5)
1
2

下面，我们使用切比雪夫多项式重新对数据进行插值。

A = P.chebyshev.chebvander(x, deg)
A
1
2

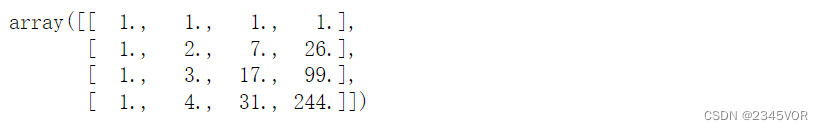
c = linalg.solve(A, y)
c
1
2

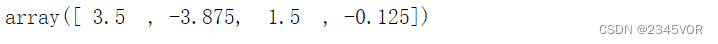
f2 = P.Chebyshev(c)
f2(2.5)
1
2

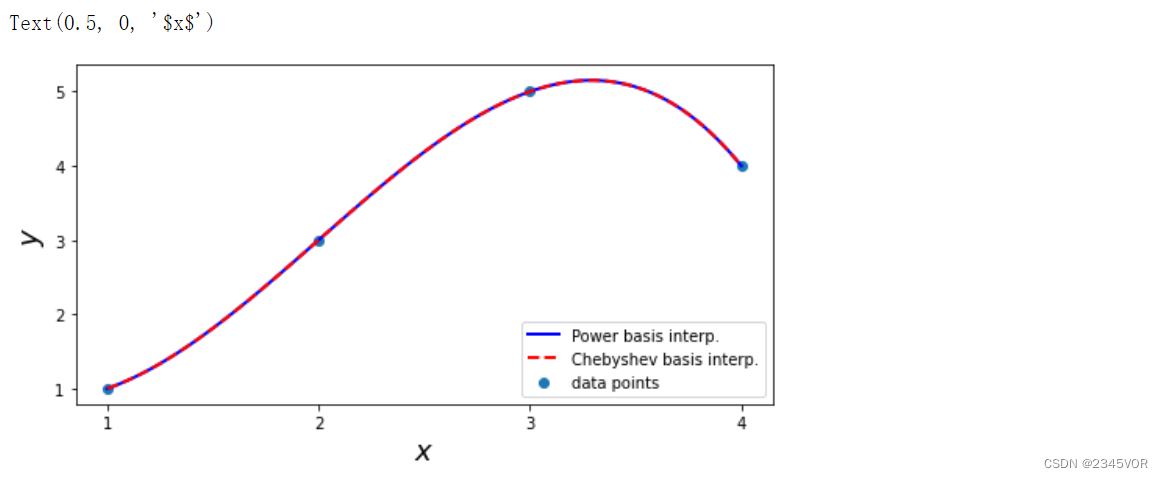
将函数$f1$和$f2$进行对比，验证不同基函数进行插值，得到了一致的插值函数。

xx = np.linspace(x.min(), x.max(), 100)

fig, ax = plt.subplots(1, 1, figsize=(8, 4))

ax.plot(xx, f1(xx), 'b', lw=2, label='Power basis interp.')
ax.plot(xx, f2(xx), 'r--', lw=2, label='Chebyshev basis interp.')
ax.scatter(x, y, label='data points')

ax.legend(loc=4)
ax.set_xticks(x)
ax.set_ylabel(r"$y$", fontsize=18)
ax.set_xlabel(r"$x$", fontsize=18)
1
2
3
4
5
6
7
8
9
10
11
12

polynomial模块还提供了更快捷的方法计算插值多项式。每个多项式类都有fit方法用于计算插值，deg参数用于控制多项式的次数。如果多项式的次数少于数据点的数目减1，fit方法会使用最小二乘拟合而不是精确插值。

f1b = P.Polynomial.fit(x, y, deg)
f1b
1
2

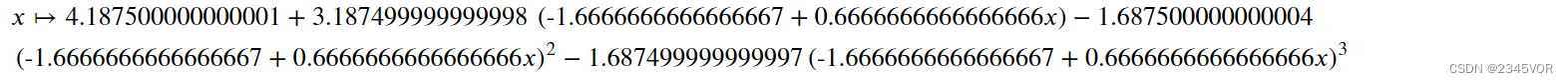
f2b = P.Chebyshev.fit(x, y, deg)
f2b
1
2

注意在使用fit方法时，实例中的domain属性会自动设置为数据点中相应的x值，上述示例中为[1, 4]，并相应调整系数。将插值数据映射到某个基函数最合适的范围，可以明显提高插值的数值稳定性，减小范德蒙矩阵的条件数。

np.linalg.cond(P.chebyshev.chebvander(x, deg))
1

np.linalg.cond(P.chebyshev.chebvander((2*x-5)/3.0, deg))
1

当数据点的数量增加时，需要使用次数更多的多项式才能得到精确的插值。这会带来多方面问题：

1. 次数更多的多项式插值计算和插值函数的确定，计算量很大。
2. 高次多项式插值可能会在插值点之间带来不可预料的行为，插值函数在数据点之间可能变化很大。
   下面我们将使用龙格函数演示这种行为：

def runge(x):
    return 1/(1 + 25 * x**2)

def runge_interpolate(n):
    x = np.linspace(-1, 1, n+1)
    p = P.Polynomial.fit(x, runge(x), deg=n)
    return x, p

xx = np.linspace(-1, 1, 250)

fig, ax = plt.subplots(1, 1, figsize=(8, 4))

ax.plot(xx, runge(xx), 'k', lw=2, label="Runge's function")

n = 13
x, p = runge_interpolate(n)
ax.plot(x, runge(x), 'ro')
ax.plot(xx, p(xx), 'r', label='interp. order %d' % n)

n = 14
x, p = runge_interpolate(n)
ax.plot(x, runge(x), 'go')
ax.plot(xx, p(xx), 'g', label='interp. order %d' % n)

ax.legend(loc=8)
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(-1, 2)
ax.set_xticks([-1, -0.5, 0, 0.5, 1])
ax.set_ylabel(r"$y$", fontsize=18)
ax.set_xlabel(r"$x$", fontsize=18)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

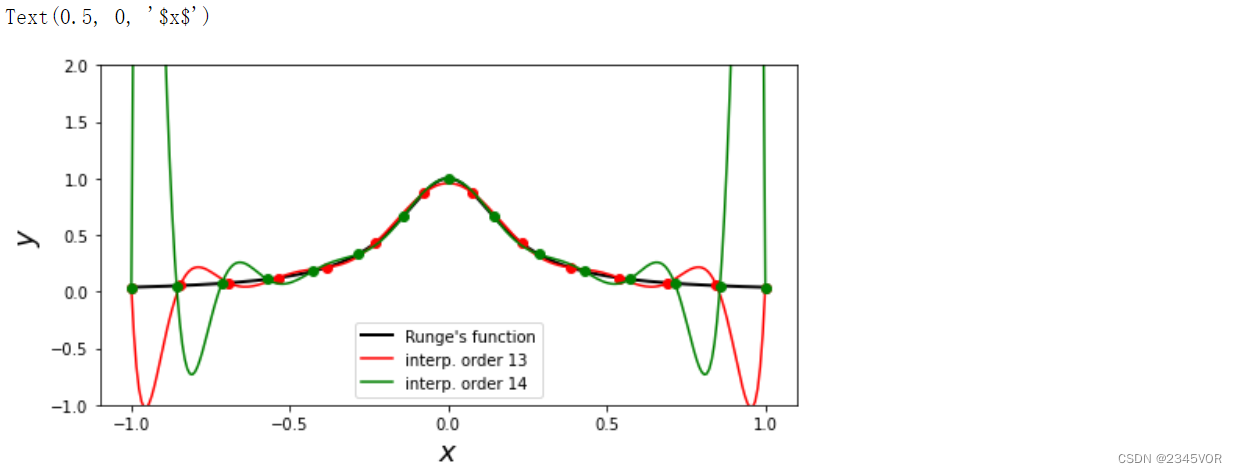
可以看到，高阶插值函数在远端采样点之间急剧震荡。这种不良特性违背了插值的初衷。一个可行的解决方法是，当面对大量数据点时，使用分段低次多项式进行插值。

3.3 样条插值

---

对于包含$n$个数据点的集合，在整个数据区间上有$n-1$个子区间。连接两个子区间的数据点在分段多项式插值中被称为节点。在每个子区间上使用$k$次多项式对$n$个数据点进行插值，需要确定$(k+1)(n-1)$个参数。所有节点的值可以给出$2(n-1)$个方程。为了保证分段多项式的平滑，节点处导数和高阶导数的连续性也会给出相应方程。

样条是一种特殊类型的分段式插值函数。最常用的是三次样条，$k=3$，需要$4(n-1)$个参数。在$n-2$个节点处，一阶和二阶导数的连续性可以给出$2(n-1)$个方程，总方程的数目为$4(n-1)-2$。此时还剩下两个未确定的参数。一种常见的方法是要求端点处的二阶导数为0，这被称为自然样条。

SciPy的interpolate模块提供了用于样条插值的多个函数和类。下面我们将再次使用龙格函数，演示使用interpolate.interp1d函数。这里设置kind=3来计算三次样条。

x = np.linspace(-1, 1, 11)
y = runge(x)
f = interpolate.interp1d(x, y, kind=3)
f(0.05)
1
2
3
4

xx = np.linspace(-1, 1, 100)
fig, ax = plt.subplots(figsize=(8, 4))

ax.plot(xx, runge(xx), 'k', lw=1, label="Runge's function")
ax.plot(x, y, 'ro', label='sample points')
ax.plot(xx, f(xx), 'r--', lw=2, label='spline order 3')

ax.legend()
ax.set_ylim(0, 1.1)
ax.set_xticks([-1, -0.5, 0, 0.5, 1])
ax.set_ylabel(r"$y$", fontsize=18)
ax.set_xlabel(r"$x$", fontsize=18)
1
2
3
4
5
6
7
8
9
10
11
12

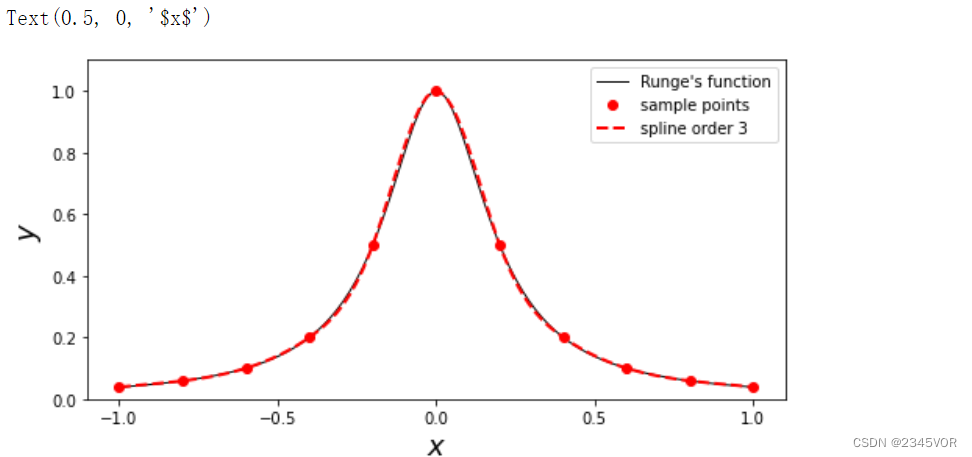
这里使用了11个数据点和三次样条，可以看到插值很好地与原始函数吻合。
为了说明阶数对样条插值的影响，我们下面准备了8个数据点使用不同阶数的样条进行插值。

x = np.array([0, 1, 2, 3, 4, 5, 6, 7])
y = np.array([3, 4, 3.5, 2, 1, 1.5, 1.25, 0.9])

xx = np.linspace(x.min(), x.max(), 100)

fig, ax = plt.subplots(figsize=(8, 4))

ax.scatter(x, y)

for n in [1, 2, 3, 5]:
    f = interpolate.interp1d(x, y, kind=n)
    ax.plot(xx, f(xx), label='order %d' % n)

ax.legend()
ax.set_ylabel(r"$y$", fontsize=18)
ax.set_xlabel(r"$x$", fontsize=18)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

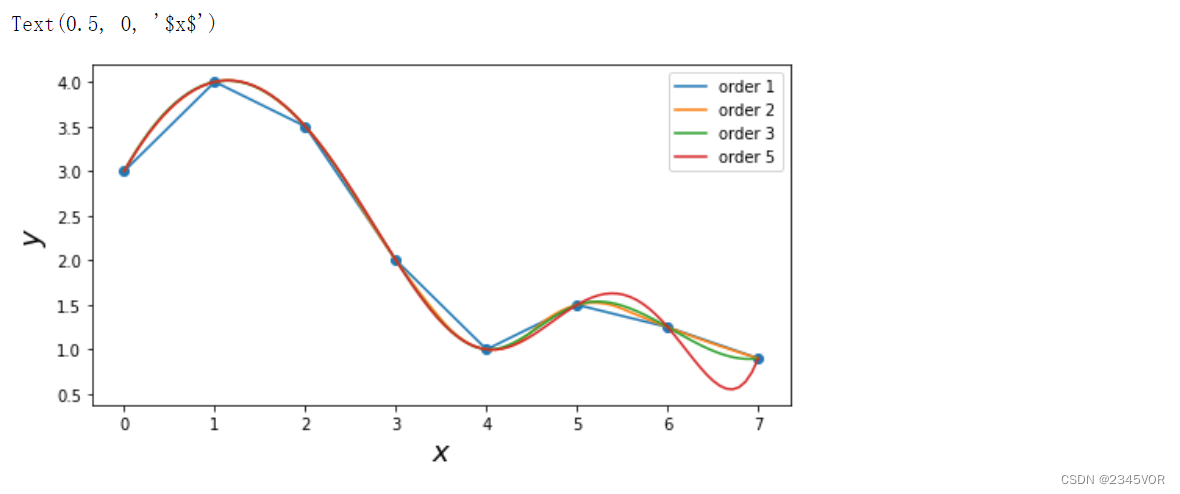
可以看到，二阶或三阶样条已经能够提供较好的插值。高阶样条会出现高阶多项式插值中类似的数值震荡问题。

3.4 多变量插值

---

多项式插值和样条插值都可以直接推广到多变量情况。SciPy为多变量插值提供了多个函数和类。我们将介绍两个最常用的双变量插值函数：interpolate.interp2d和interpolate.griddata。

3.4.1 均匀网格

interpolate.interp2d函数是interpolate.interp1d函数的推广，要求数据点位于x和y坐标组成的规则且均匀的网格中。

为了演示函数用法，我们在已知函数
$$f(x,y)=\exp (-(x+1/2{)}^2-2(y+1/2{)}^2)-\exp (-(x-1/2{)}^2-2(y-1/2{)}^2)$$
中添加随机噪声来模拟测量噪声。为了构造插值问题，我们在x和y坐标的[-2, 2]区间上采样10个点。

def f(x, y):
    return np.exp(-(x + .5)**2 - 2*(y + .5)**2) - np.exp(-(x - .5)**2 - 2*(y - .5)**2)

x = y = np.linspace(-2, 2, 10)
X, Y = np.meshgrid(x, y)
# simulate noisy data at fixed grid points X, Y
Z = f(X, Y) + 0.05  * np.random.randn(*X.shape)
f_interp = interpolate.interp2d(x, y, Z, kind='cubic')  # 三次样条插值
xx = yy = np.linspace(x.min(), x.max(), 100)
ZZ_interp = f_interp(xx, yy)
XX, YY = np.meshgrid(xx, yy)

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

c = axes[0].contourf(XX, YY, f(XX, YY), 15, cmap=plt.cm.RdBu)
axes[0].set_xlabel(r"$x$", fontsize=20)
axes[0].set_ylabel(r"$y$", fontsize=20)
axes[0].set_title("exact / high sampling")
cb = fig.colorbar(c, ax=axes[0])
cb.set_label(r"$z$", fontsize=20)

c = axes[1].contourf(XX, YY, ZZ_interp, 15, cmap=plt.cm.RdBu)
axes[1].set_ylim(-2.1, 2.1)
axes[1].set_xlim(-2.1, 2.1)
axes[1].set_xlabel(r"$x$", fontsize=20)
axes[1].set_ylabel(r"$y$", fontsize=20)
axes[1].scatter(X, Y, marker='x', color='k')
axes[1].set_title("interpolation of noisy data / low sampling")
cb = fig.colorbar(c, ax=axes[1])
cb.set_label(r"$z$", fontsize=20)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

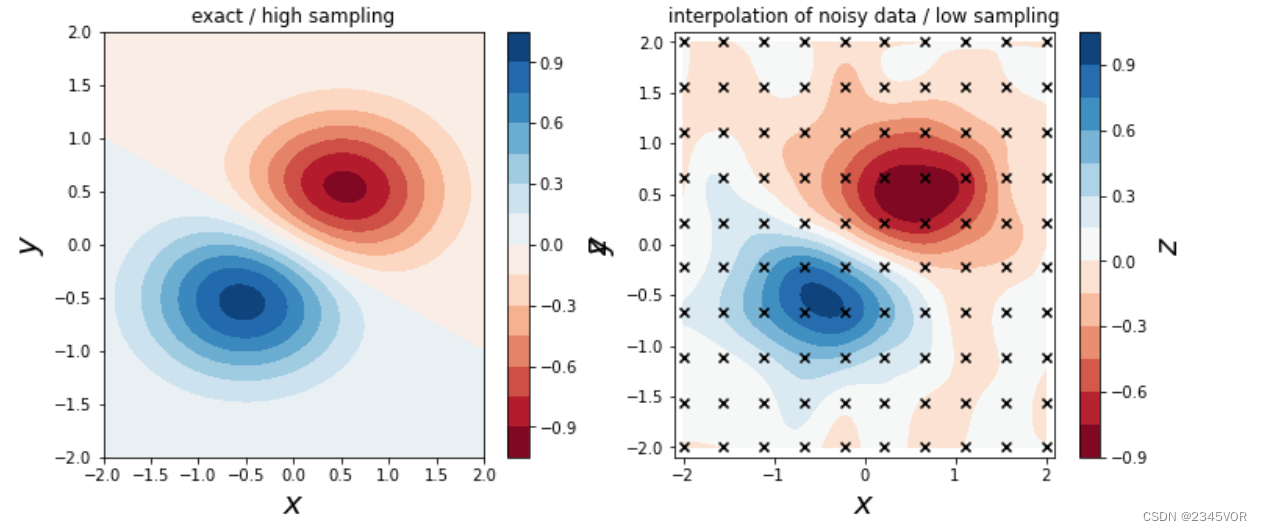
对于更高维的问题，可以使用interpolate.interpnd函数，它是对N维问题的推广。

3.4.2 不均匀网格

另一种多变量插值的常见场景是从不规则的坐标网络中采样数据，例如实验室数据等。为了能够使用现有的工具对数据进行可视化分析，可能需要将它们插值到规则的坐标网格中。

在SciPy中，可以使用interpolate.griddata函数来完成这项工作。该函数的第一个参数是坐标向量构成的元组，第二个参数是对应的数据点的值，第三个参数是待插值的新数据点的坐标数组或坐标矩阵。
我们考虑函数$f(x,y)=\exp (-x^2-y^2)\cos 4x\sin 6y$在x和y坐标区间[-1, 1]上随机选择的采样点，并对采样数据进行插值。

def f(x, y):
    return np.exp(-x**2 - y**2) * np.cos(4*x) * np.sin(6*y)

x = y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
np.random.seed(0)
N = 500
xdata = np.random.uniform(-1, 1, N)
ydata = np.random.uniform(-1, 1, N)
zdata = f(xdata, ydata)
1
2
3
4
5
6
7
8
9
10
11

我们画出函数 声明：本文内容由网友自发贡献，转载请注明出处：【wpsshop】