动态规划也是一种分治思想，但与分治算法不同的是，分治算法是把原问题分解成若干子问题，自顶向下求解各子问题，合并子问题的解，从而得到原问题的解。动态规划也是把原问题分解为若干子问题然后自底向上，先求解最小的子问题，把结果存储在表格中，再求解大的子问题时，直接从表格中查询小的子问题的解，避免重复计数，从而提高算法效率。

二、解题步骤

（1）分析最优解的结构特征

（2）建立最优值的递归式

（3）自底向上计算最优值，并记录

（4）构造最优解

三、神奇的兔子序列

（一）问题

前两个月都是1对兔子，从第3个月开始，当月的兔子数等于前两个月的兔子数，求解第n个月的兔子数量？

（二）递归公式

$F(n)=\begin{cases}1 & n = 1,n=2\\F(n-1)+F(n-2) & n > 2\end{cases}$

（三）以求解F(6)为例

利用动态规划求解的时候，记录结果，重复问题只需要求解依次即可

（四）代码


int Fib(int n)
{
	if (n < 1)
		return -1;
	else
	{
		vector<int>F(n+1);
		F[0]=0;
		F[1]=1;
		F[2]=1;
		for (int i = 3; i <= n; i++)
		{
			F[i] = F[i - 1] + F[i - 2];
		}
		return F[n];
	}
}

四、01背包问题

（一）算法思想

用数组 $dp[i][j]$ 表示从下标为0到 $i-1$ 的物品里任意选取，然后放进容量为 $j$ 的背包中，背包所能装入的最大价值。

对于一个物品i，要么能放入背包，要么不能放入背包：

第一种情况：物品 $i$ 的重量 $w[i]$ 大于背包容量 $j$ 的时候，此时物品 $i$ 不能放入背包中，那么需要从剩下0到 $i-1$ 个物品中任意选取放入背包中，此时背包所能装入最大价值为 $dp[i][j]=dp[i-1][j]$ 。
第二种情况：物品 $i$ 的重量 $w[i]$ 小于背包容量的时候，此时物品 $i$ 能放入背包中，但是可以选择将物品 $i$ 不放入背包或者放入背包。第二种情况又分以下两种：
1.选择不将物品 $i$ 放入背包的时候，那么从剩下的0到 $i-1$ 个物品中任意选取价值大的物品放入背包中，此时背包所能装入最大价值为 $dp[i][j]=dp[i-1][j]$ 。
2.选择将物品 $i$ 放入背包的时候，需要先将物品 $i$ 放入背包，那么背包剩余容量为 $j-w[i]$ ，
此时从剩下的0到 $i-1$ 个物品中任意选取价值大的物品放入背包中，背包所能装入最大价值为 $dp[i][j]=dp[i-1][j-w[i]]+v[i]$
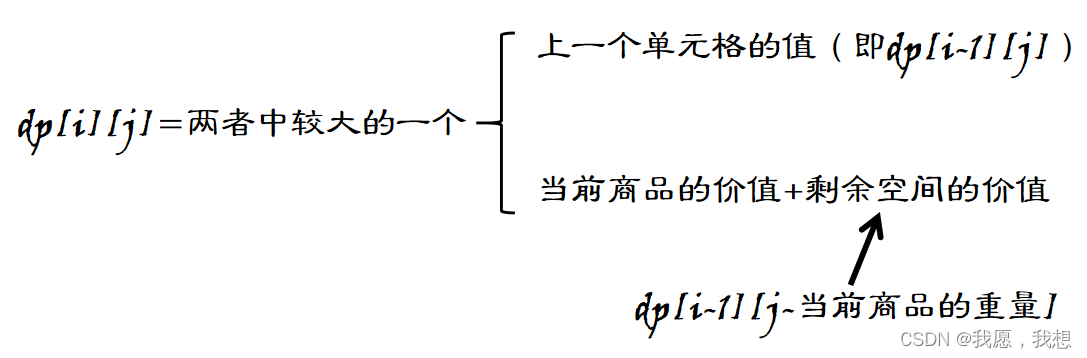
那么物品最大价值为： $dp[i][j]=max\left \{ dp[i-1][j],dp[i-1][j-w[i]]+v[i] \right \}$

所以背包所能装入最大价值为：

$dp[i][j]=\begin{cases}dp[i-1][j] &,0<= j<w[i]\\max \left \{ dp[i-1][j] ,dp[i-1][j-w[i]]+v[i]\right \}&, j>=w[i]\end{cases}$

（二）举例

1. 有3种物品

物品	价值	重量
吉他	1500美元	1磅
音箱	3000美元	4磅
笔记本电脑	2000美元	3磅

2. 背包问题网格

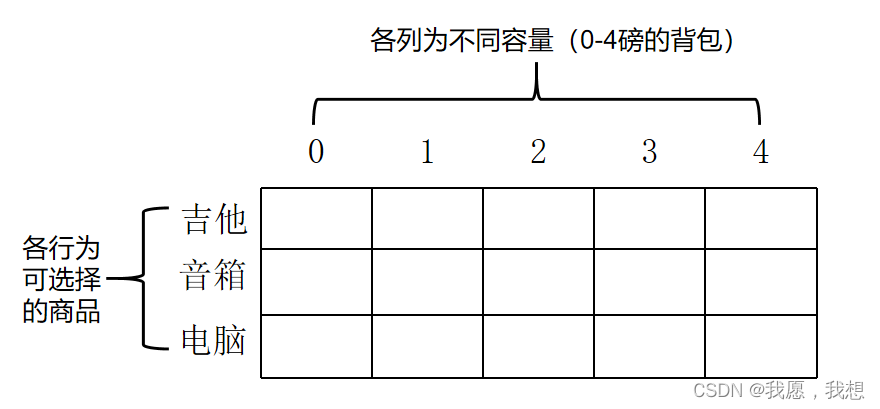
3. 初始化第一列

背包容量为0，意味着吉他，音箱，电脑都不能装入背包，所有此时背包最大价值均为0

4. 吉他行

1. 第2个单元格表示背包的容量为1磅。吉他的重量也是1磅，这意味着它能装入背包！

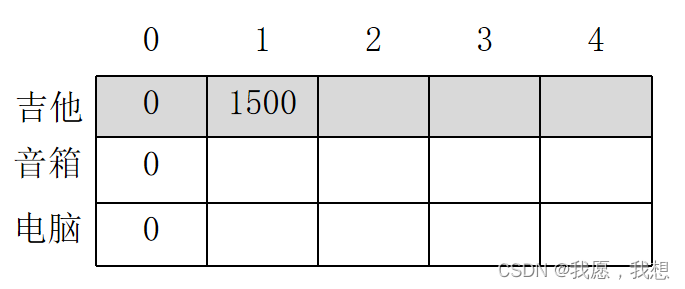
2. 之后背包容量为2磅，3磅，4磅也能装下

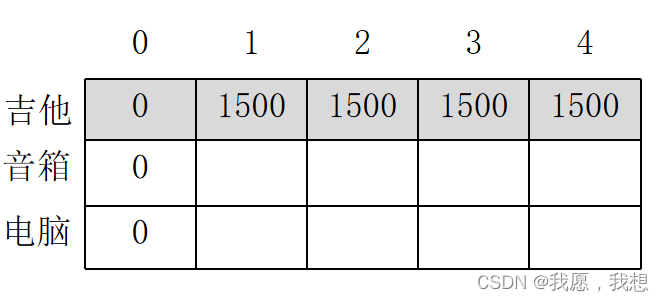
3. 表明若一个背包容量为4磅，可在其中装入的商品的最大价值为1500美元

5. 音箱行

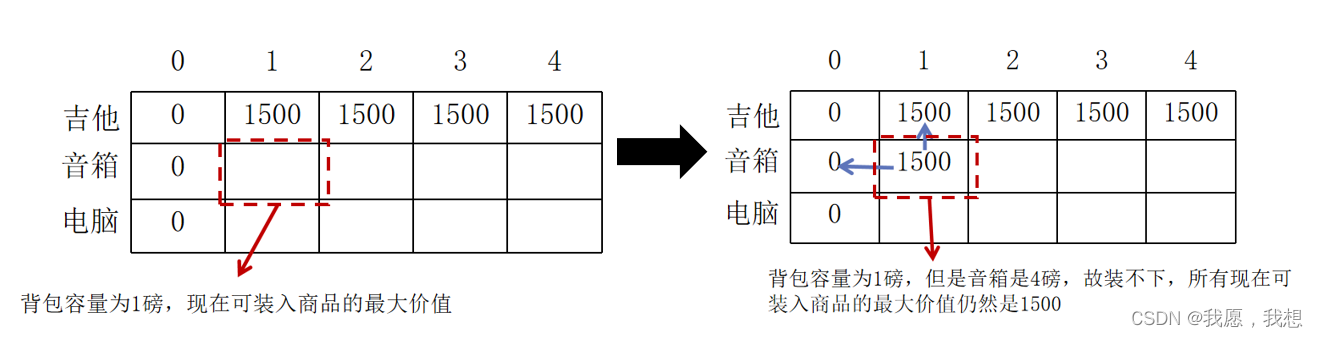
更新最大值：表明若一个背包容量为4磅，可在其中装入的商品的最大价值为3000美元

6. 电脑行

7. 总结

（三）核心代码


template<typename T1,typename T2>
void Knapsack(int bagW,int n)
{
	vector<T1>value(n);//存放物品价值
	vector<T2>weight(n);//物品数量
	Init(n,value,weight);//初始化物品信息
	vector<vector<T1>>dp(n,vector<T1>(bagW+1,0));//背包最大价值
 
	for (int i = 0; i < n; i++)//初始化第一列
	{
		dp[i][0] = 0;
	}
	for (int j = 1; j <= bagW; j++)//初始化第一行
	{
		if (j < weight[0])//背包容量小于物品重量
			dp[0][j] = 0;
		else
			dp[0][j] = value[0];
	}
 
	for (int i = 1; i < n; i++)//i是物品序号
	{
		for (int j = 1; j <=bagW; j++)//j表示背包容量
		{
			if (j < weight[i])//容量为j的背包装不了物品i
				dp[i][j] = dp[i - 1][j];//此时背包最大价值为前i-1个物品的最大价值
			else
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
		}
	}
	cout << "背包最大价值："<<dp[n - 1][bagW];
}

（四）完整代码


#include<iostream>
#include<vector>
using namespace std;
template<typename T1, typename T2>
void Init(int n,vector<T1>&v,vector<T2>&w)//物品初始化
{
	cout << "依次输入物品的价值和重量："<<endl;
	for (int i = 0; i < n; i++)
	{
		cin >> v[i] >> w[i];
	}
	//直接初始化物品
	//vector<T1>value{ 1501.6,3000,2000.8 };
	//v = value;
	//vector<T2>weight{ 1,4,3 };
	//w = weight;
}
template<typename T1,typename T2>
void Knapsack(int bagW,int n)
{
	vector<T1>value(n);//存放物品价值
	vector<T2>weight(n);//物品数量
	Init(n,value,weight);//初始化物品信息
	vector<vector<T1>>dp(n,vector<T1>(bagW+1,0));//背包最大价值
 
	for (int i = 0; i < n; i++)//初始化第一列
	{
		dp[i][0] = 0;
	}
	for (int j = 1; j <= bagW; j++)//初始化第一行
	{
		if (j < weight[0])//背包容量小于物品重量
			dp[0][j] = 0;
		else
			dp[0][j] = value[0];
	}
 
	for (int i = 1; i < n; i++)//i是物品序号
	{
		for (int j = 1; j <=bagW; j++)//j表示背包容量
		{
			if (j < weight[i])//容量为j的背包装不了物品i
				dp[i][j] = dp[i - 1][j];//此时背包最大价值为前i-1个物品的最大价值
			else
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
		}
	}
	cout << "背包最大价值："<<dp[n - 1][bagW];
}
 
int main()
{
	Knapsack<float,int>(4,3);//背包最大容量为4，物品个数为3
	return 0;
}

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/144257