一文带你读懂深度学习中的张量（tensor）是什么，它的运算是怎样的，如何理解张量，张量的维度，浅显易懂_深度学习张量

深度学习的数学基础（不要被吓到，很浅显）

数据表示与张量运算

张量

在多维 Numpy 数组中，也叫张量（tensor）。一般来说，当前所有机器学习系统都使用张量作为基本数据结构。

张量这一概念的核心在于，它是一个数据容器。它包含的数据几乎总是数值数据，因此它是数字的容器。你可能对矩阵很熟悉，它是二维张量。张量是矩阵向任意维度的推广［注意，张量的维度（dimension）通常叫作轴（axis）］

0. scalar 标量 0D张量

仅包含一个数字的张量叫作标量（scalar，也叫标量张量、零维张量、0D 张量）。在 Numpy中，一个 float32 或 float64 的数字就是一个标量张量（或标量数组）。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴（ndim == 0）。张量轴的个数也叫作阶（rank）。下面是一个 Numpy 标量。

1. vector 向量 1D张量

数字组成的数组叫作向量（vector）或一维张量（1D 张量）。一维张量只有一个轴。下面是一个 Numpy 向量。

\>>> x = np.array([12, 3, 6, 14, 7])

\>>> x

array([12, 3, 6, 14, 7])

\>>> x.ndim

1
1
2
3
4
5
6
7
8
9

这个向量有 5 个元素，所以被称为 5D 向量。不要把 5D 向量和 5D 张量弄混！ 5D 向量只有一个轴，沿着轴有 5 个维度，而 5D 张量有 5 个轴（沿着每个轴可能有任意个维度）。维度（dimensionality）可以表示沿着某个轴上的元素个数（比如 5D 向量），也可以表示张量中轴的个数（比如 5D 张量），这有时会令人感到混乱。对于后一种情况，技术上更准确的说法是 5 阶张量（张量的阶数即轴的个数），但 5D 张量这种模糊的写法更常见。

补充：来自吴恩达《机器学习》
Vector ： An n x 1 matrix
向量是一个只有一列的矩阵

2. matrix 矩阵 2D张量

\>>> x = np.array([[5, 78, 2, 34, 0],

 [6, 79, 3, 35, 1],

 [7, 80, 4, 36, 2]])

\>>> x.ndim

2
1
2
3
4
5
6
7
8
9

第一个轴上的元素叫作行（row），第二个轴上的元素叫作列（column）。在上面的例子中，[5, 78, 2, 34, 0] 是 x 的第一行，[5, 6, 7] 是第一列。

关键属性

• 轴的个数（阶）。例如，3D 张量有 3 个轴，矩阵有 2 个轴。这在 Numpy 等 Python 库中也叫张量的 ndim。
• 形状。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。例如，前面矩阵示例的形状为 (3, 5)，3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个元素，比如 (5,)，而标量的形状为空，即 ()。
• 数据类型（在 Python 库中通常叫作 dtype）。这是张量中所包含数据的类型，例如，张量的类型可以是 float32、uint8、float64 等。在极少数情况下，你可能会遇到字符（char）张量。注意，Numpy（以及大多数其他库）中不存在字符串张量，因为张量存储在预先分配的连续内存段中，而字符串的长度是可变的，无法用这种方式存储。

矩阵加法

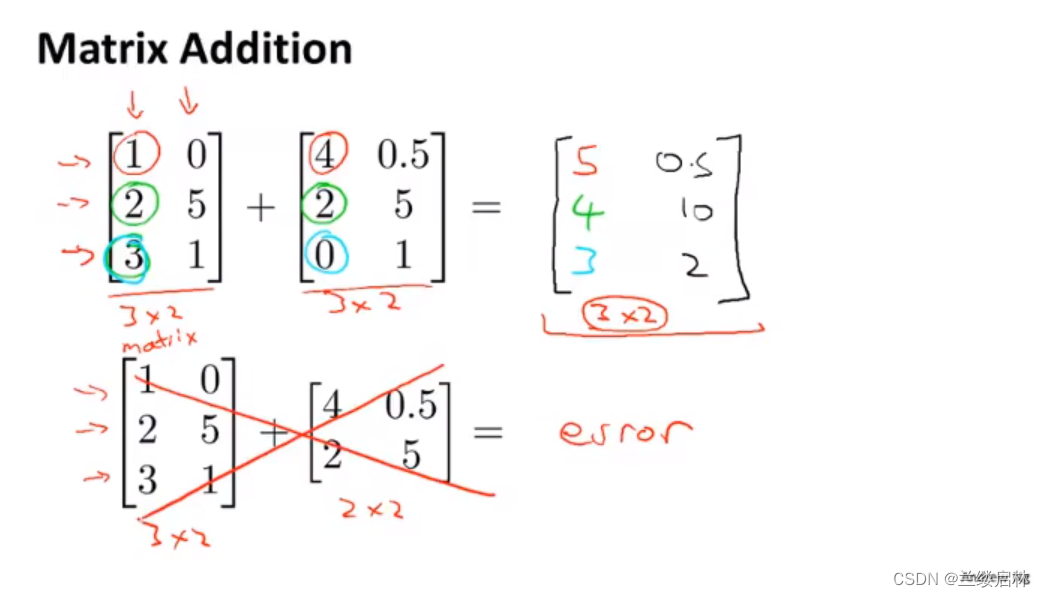
乘标量

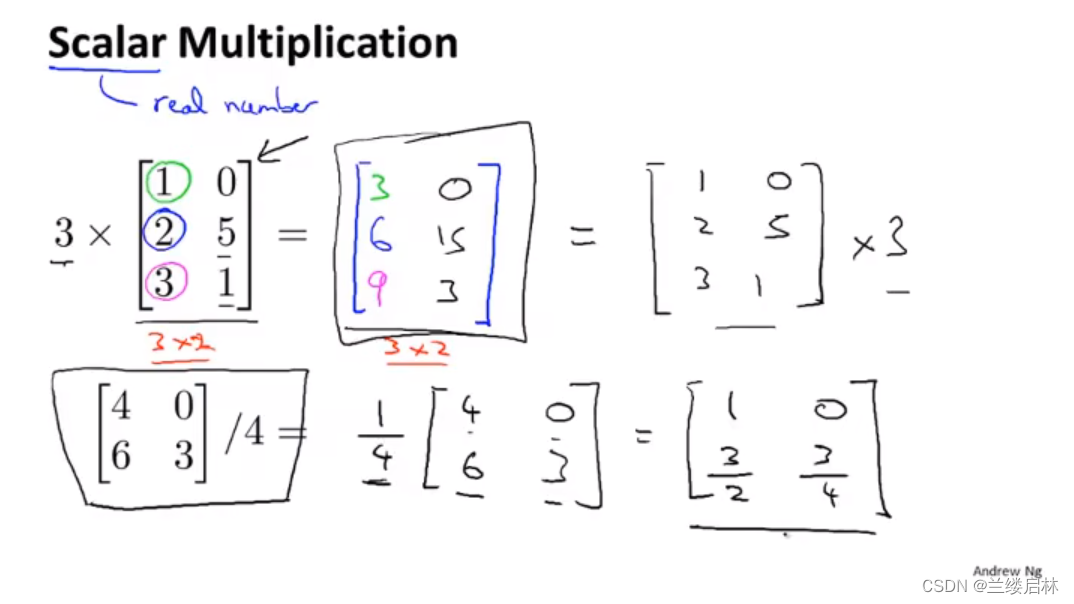
矩阵乘法

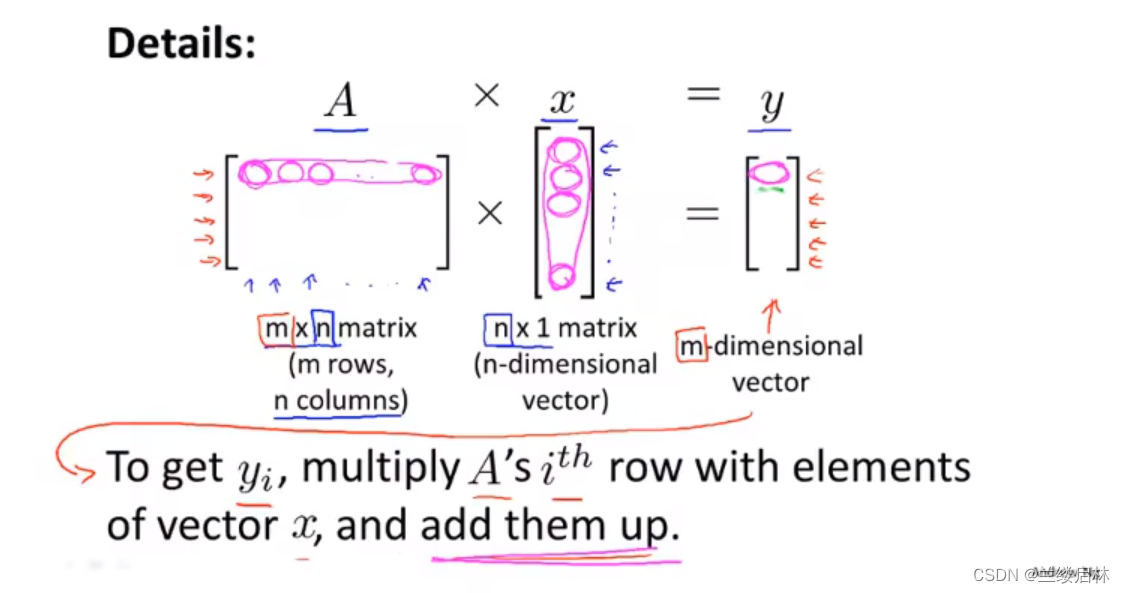
程序实现预测多个房子价格的技巧：用矩阵运算，而不用for，计算效率更高

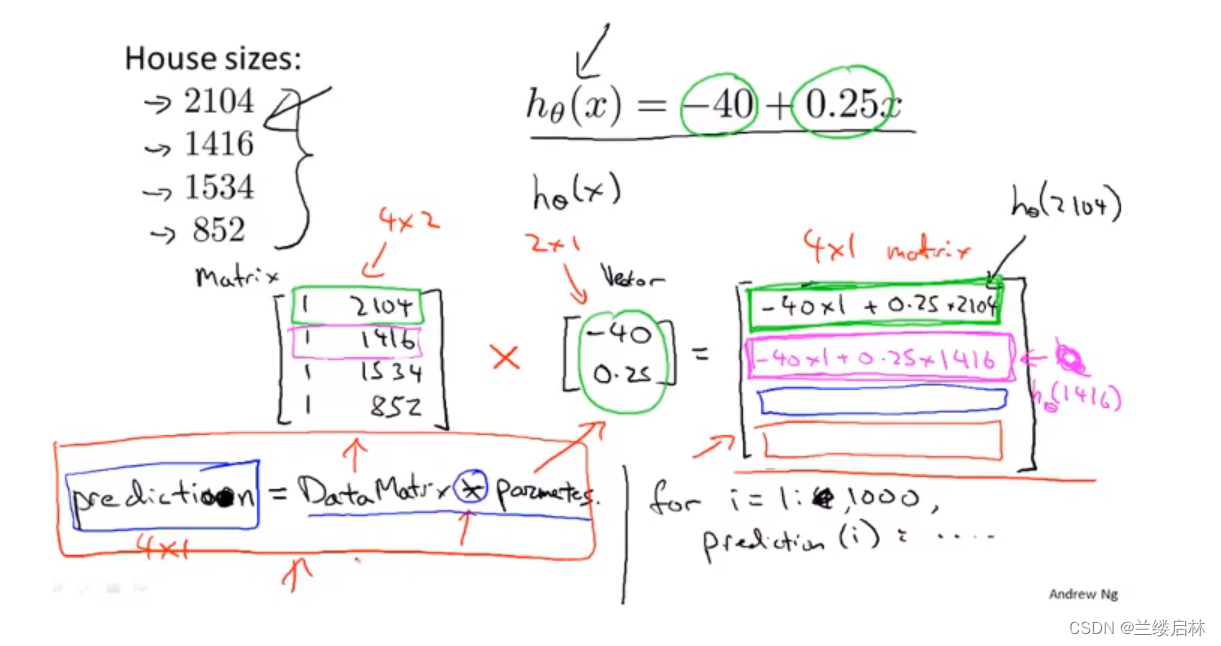
有多组可能参数的用矩阵乘矩阵，（相当于把第二个矩阵拆成若干个列向量）

数据批量

通常来说，深度学习中所有数据张量的第一个轴（0 轴，因为索引从 0 开始）都是样本轴（samples axis，有时也叫样本维度）。

对于这种批量张量，第一个轴（0 轴）叫作批量轴（batch axis）或批量维度（batch dimension）。

batch = train_images[:128]

batch = train_images[128:256]

batch = train_images[128 * n:128 * (n + 1)]
1
2
3
4
5

现实世界的数据张量

‰ 向量数据：2D 张量，形状为 (samples, features)。

‰ 时间序列数据或序列数据：3D 张量，形状为 (samples, timesteps, features)。

‰ 图像：4D 张量，形状为 (samples, height, width, channels) 或 (samples, channels,

height, width)。

‰ 视频：5D 张量，形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)。

向量数据

这是最常见的数据。对于这种数据集，每个数据点都被编码为一个向量，因此一个数据批量就被编码为 2D 张量（即向量组成的数组），其中第一个轴是样本轴，第二个轴是特征轴。

• 人口统计数据集，其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量，而整个数据集包含 100 000 个人，因此可以存储在形状为 (100000, 3) 的 2D张量中。
• 文本文档数据集，我们将每个文档表示为每个单词在其中出现的次数（字典中包含20 000 个常见单词）。每个文档可以被编码为包含 20 000 个值的向量（每个值对应于字典中每个单词的出现次数），整个数据集包含 500 个文档，因此可以存储在形状为(500, 20000) 的张量中。

时间序列数据或序列数据

当时间（或序列顺序）对于数据很重要时，应该将数据存储在带有时间轴的 3D 张量中。

每个样本可以被编码为一个向量序列（即 2D 张量），因此一个数据批量就被编码为一个 3D 张量。

根据惯例，时间轴始终是第 2 个轴（索引为 1 的轴）。我们来看几个例子。

• 股票价格数据集。每一分钟，我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个 3D 向量，整个交易日被编码为一个形状为 (390, 3) 的 2D 张量（一个交易日有 390 分钟），而 250 天的数据则可以保存在一个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
• 推文数据集。我们将每条推文编码为 280 个字符组成的序列，而每个字符又来自于 128个字符组成的字母表。在这种情况下，每个字符可以被编码为大小为 128 的二进制向量（只有在该字符对应的索引位置取值为 1，其他元素都为 0）。那么每条推文可以被编码为一个形状为 (280, 128) 的 2D 张量，而包含 100 万条推文的数据集则可以存储在一个形状为 (1000000, 280, 128) 的张量中。

图像数据

图像通常具有三个维度：高度、宽度和颜色深度

虽然灰度图像（比如 MNIST 数字图像）只有一个颜色通道，因此可以保存在 2D 张量中，但按照惯例，图像张量始终都是 3D 张量，灰度图像的彩色通道只有一维。因此，如果图像大小为 256×256，那么 128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中，而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中。

图像张量的形状有两种约定：通道在后（channels-last）的约定（在 TensorFlow 中使用）和通道在前（channels-first）的约定（在 Theano 中使用）。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后：(samples, height, width, color_depth)。与此相反，Theano将图像深度轴放在批量轴之后：(samples, color_depth, height, width)。如果采用 Theano 约定，前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。Keras 框架同时支持这两种格式。

视频数据

视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧，每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_depth) 的 3D 张量中，因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中，而不同视频组成的批量则可以保存在一个 5D 张量中，其形状为**(samples, frames, height, width, color_depth)**。

举个例子，一个以每秒 4 帧采样的 60 秒 YouTube 视频片段，视频尺寸为 144×256，这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中。总共有 106 168 320 个值！如果张量的数据类型（dtype）是 float32，每个值都是32 位，那么这个张量共有 405MB。好大！你在现实生活中遇到的视频要小得多，因为它们不以float32 格式存储，而且通常被大大压缩，比如 MPEG 格式。

张量运算

逐元素计算

relu 运算和加法都是**逐元素（element-wise）**的运算，即该运算独立地应用于张量中的每个元素，也就是说，这些运算非常适合大规模并行实现（向量化实现，这一术语来自于 1970—1990 年间向量处理器超级计算机架构）

def naive_relu(x):
 assert len(x.shape) == 2 
 x = x.copy() 
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] = max(x[i, j], 0)
 return x

def naive_add(x, y):
 assert len(x.shape) == 2 
 assert x.shape == y.shape
 x = x.copy() 
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] += y[i, j]
 return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

根据同样的方法，你可以实现逐元素的乘法、减法等

广播

上一节 naive_add 的简单实现仅支持两个形状相同的 2D 张量相加。但在前面介绍的Dense 层中，我们将一个 2D 张量与一个向量相加。如果将两个形状不同的张量相加，如果没有歧义的话，较小的张量会被广播（broadcast），以匹配较大张量的形状。

• (1) 向较小的张量添加轴（叫作广播轴），使其 ndim 与较大的张量相同。
• (2) 将较小的张量沿着新轴重复，使其形状与较大的张量相同。

来看一个具体的例子。假设 X 的形状是 (32, 10)，y 的形状是 (10,)。首先，我们给 y

添加空的第一个轴，这样 y 的形状变为 (1, 10)。然后，我们将 y 沿着新轴重复 32 次，这样得到的张量 Y 的形状为 (32, 10)，并且 Y[i, :] == y for i in range(0, 32)。现在，我们可以将 X 和 Y 相加，因为它们的形状相同。

在实际的实现过程中并不会创建新的 2D 张量，因为那样做非常低效。重复的操作完全是虚拟的，它只出现在算法中，而没有发生在内存中。但想象将向量沿着新轴重复 10 次，是一种很有用的思维模型。下面是一种简单的实现。

def naive_add_matrix_and_vector(x, y):
 assert len(x.shape) == 2 
 assert len(y.shape) == 1 
 assert x.shape[1] == y.shape[0]
 x = x.copy() 
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] += y[j]
 return x
1
2
3
4
5
6
7
8
9

张量点积

点积运算，也叫张量积（tensor product，不要与逐元素的乘积弄混），是最常见也最有用的张量运算。与逐元素的运算不同，它将输入张量的元素合并在一起。

Numpy、Keras、Theano 和 TensorFlow 中，都是用 *** 实现逐元素乘积**。TensorFlow 中的点积使用了不同的语法，但在 Numpy 和 Keras 中，都是用标准的 dot 运算符来实现点积。

import numpy as np

z = np.dot(x, y)
1
2
3

数学符号中的点（.）表示点积运算。

z=x.y

两个向量的点积是一个标量

矩阵和向量的点积是一个向量

点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。对于两个矩阵 x 和 y，当且仅当 x.shape[1] == y.shape[0] 时，你才可以对它们做点积（dot(x, y)）。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵

更一般地说，你可以对更高维的张量做点积，只要其形状匹配遵循与前面 2D 张量相同的原则：

• (a, b, c, d) . (d,) -> (a, b, c)

• (a, b, c, d) . (d, e) -> (a, b, c, e)

张量变形

reshape

>>> x = np.array([[0., 1.],
 [2., 3.],
 [4., 5.]])
>>> print(x.shape)
(3, 2)
>>> x = x.reshape((6, 1))
1
2
3
4
5
6

转置transpose

>>> x = np.zeros((300, 20)) 
>>> x = np.transpose(x)
>>> print(x.shape)
(20, 300)
1
2
3
4

几何解释

张量的几何解释

对于张量运算所操作的张量，其元素可以被解释为某种几何空间内点的坐标

两个张量相加。从几何上来看，这相当于将两个向量箭头连在一起，得到的位置表示两个向量之和对应的向量

通常来说，仿射变换、旋转、缩放等基本的几何操作都可以表示为张量运算。举个例子，要将一个二维向量旋转 theta 角，可以通过与一个 2×2 矩阵做点积来实现，这个矩阵为 R = [u, v]，其中 u 和 v 都是平面向量：u = [cos(theta), sin(theta)]，v = [-sin(theta), cos(theta)]。

深度学习的几何解释

现在将两张纸一起揉成小球。这个皱巴巴的纸球就是你的输入数据，每张纸对应于分类问题中的一个类别。神经网络（或者任何机器学习模型）要做的就是找到可以让纸球恢复平整的变换，从而能够再次让两个类别明确可分。通过深度学习，这一过程可以用三维空间中一系列简单的变换来实现，比如你用手指对纸球做的变换让纸球恢复平整就是机器学习的内容：为复杂的、高度折叠的数据流形找到简洁的表示。

现在你应该能够很好地理解，为什么深度学习特别擅长这一点：它将复杂的几何变换逐步分解为一长串基本的几何变换，这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通过变换使数据解开一点点——许多层堆叠在一起，可以实现非常复杂的解开过程。

基于梯度的优化

小批量随机梯度下降（mini-batch stochastic gradient descent，又称为小批量 SGD）。术语随机（stochastic）是指每批数据都是随机抽取的（stochastic 是 random在科学上的同义词 a）。

注意，小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标，而不是抽取一批数据。这叫作真 SGD（有别于小批量 SGD）。还有另一种极端，每一次迭代都在所有数据上运行，这叫作批量 SGD。这样做的话，每次更新都更加准确，但计算代价也高得多。这两个极端之间的有效折中则是选择合理的批量大小。

参考资料

本文参考自《python深度学习》