机器学习之决策树

1.决策树原理

• 决策树：树形结构流程图（漏斗型），模型本身包含一些列逻辑决策。数据分类从根节点开始，根据特征值遍历树上的各个决策节点。

• 几乎可应用于任何类型的数据建模，且性能不错。但当数据有大量多层次的名义特征或者大量的数值特征时，可能会生成一个过于复杂的决策树。

• 递归划分/分而治之：利用特征值将数据分解成具有相似类的较小的子集。

• 过程：从代表整个数据集的根节点开始，选择最能预测目标类的特征，然后将案例划分到该特征不同值的组中（即第一组树枝），继续分而治之其他节点，每次选择最佳的候选特征，直到节点上所有案例都属于同一类，或者没有其他的特征来区分案例，或者决策树已经达到了预先定义的大小。

• 由于数据可一直划分（直到组内的特征没有区别），所以决策树容易过拟合，给出过于具体细节的决策。

• C5.0决策树算法：C4.5/ID3（迭代二叉树3代）算法的改进：

  

  image.png

  ①选择最佳分割
  确定根据哪个特征来进行分割。
  纯类：一组数据中只包含单一的类。

• 熵Entropy(S)：用来度量纯度，取值0-1。0表示样本完全同质，1表示样本凌乱最大。

  

  c为类的水平，pi为落入类水平i的特征值比例

  如两个类的数据分割，红为60%，白为40%，则该数据分割的熵为：

  

  image.png

  任何可能的两个类划分的熵的图形（一个类比例x，另一个1-x）：

  curve(-x*log2(x)-(1-x)*log2(1-x),
  col=‘red’,xlab = ‘x’,ylab = ‘Entropy’,lwd=4)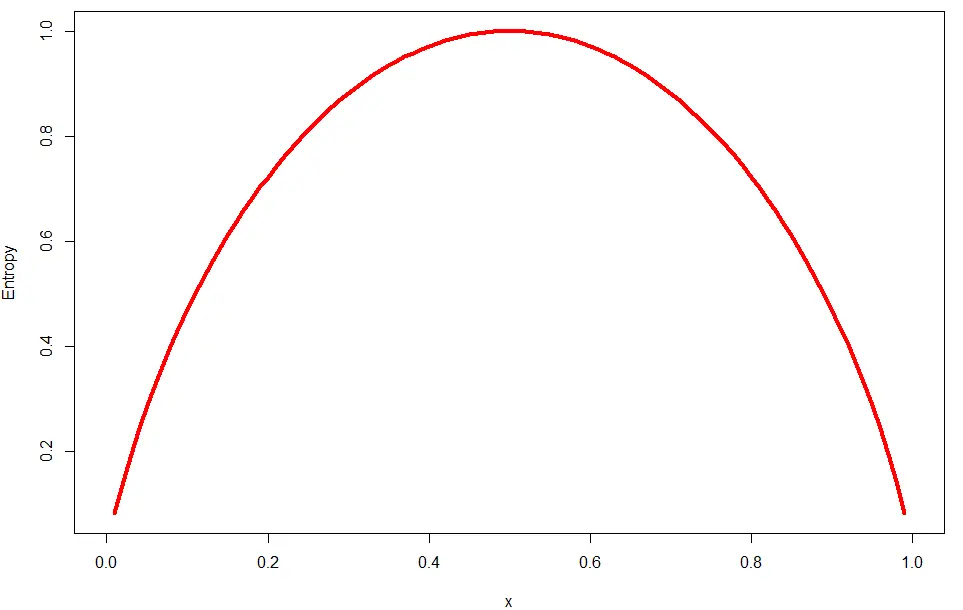

  

0.5时最大熵值

• 信息增益：用熵值计算每一个可能特征的分割引起的同质性（均匀性）变化，即分割前与分割后的数据分区熵值之差。

  

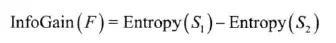
  image.png

  如果一次分割后划分到多个分区，则要通过落入每一分区比例按权重来计算所有分区熵值总和：

  

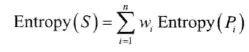
  比例wi加权的n个分区

  信息增益越高，根据某一特征分割后创建的分组越均衡。

以上假定的是名义特征，对于数值特征同样可用信息增益。即通过设置阈值来划分不同组。

除了信息增益可用于特征分割标准，其他常用的标准还有：基尼系数，卡方统计量，增益比等。

②修剪决策树

• 修建决策树减少它的大小，避免过拟合。
• 提前终止法/预剪枝决策树法：决策节点达到一定数量的案例就停止。
• 后剪枝决策树法（更有效）：根据节点处的错误率使用修剪准则将树减少到更合适的大小。
• C5.0算法能自动修剪。采用后剪枝策略，先生成一个过拟合训练集的大决策树，再删除对分类误差影响不大的节点和分枝。这样整个分枝会上移或被取代（子树提升/子树替换）。

2.决策树应用示例

采用C5.0决策树来识别高风险银行贷款

2.1）收集数据

信贷数据集：包含1000个贷款案例，贷款特征和贷款者特征的数值特征和名义特征的组合。其中一个类变量表示贷款是否陷入违约。
数据下载：

链接: https://pan.baidu.com/s/1p6eTQvUZEAHd9GaFQN0BKA 提取码: ph8u

2.2）探索和准备数据

## Example: Identifying Risky Bank Loans ----
## Step 2: Exploring and preparing the data ----
credit <- read.csv("credit.csv")
str(credit)

# look at two characteristics of the applicant
table(credit$checking_balance)
table(credit$savings_balance)

# look at two characteristics of the loan
summary(credit$months_loan_duration)
summary(credit$amount)

# look at the class variable
table(credit$default)

# create a random sample for training and test data
# use set.seed to use the same random number sequence as the tutorial
set.seed(123)
train_sample <- sample(1000, 900)

str(train_sample)

# split the data frames
credit_train <- credit[train_sample, ]
credit_test  <- credit[-train_sample, ]

# check the proportion of class variable
prop.table(table(credit_train$default))
prop.table(table(credit_test$default))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.3）训练模型

## Step 3: Training a model on the data ----
# build the simplest decision tree
library(C50)
credit_model <- C5.0(credit_train[-17], credit_train$default)
# trial可选数值用于控制自助法循环次数（默认1）
# costs可选矩阵用于给出各类型错误对应的成本

# display simple facts about the tree
credit_model

# display detailed information about the tree
summary(credit_model)
1
2
3
4
5
6
7
8
9
10
11
12

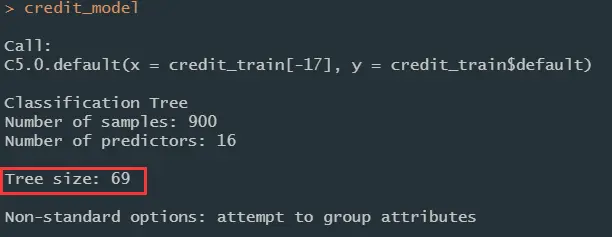
决策树大小

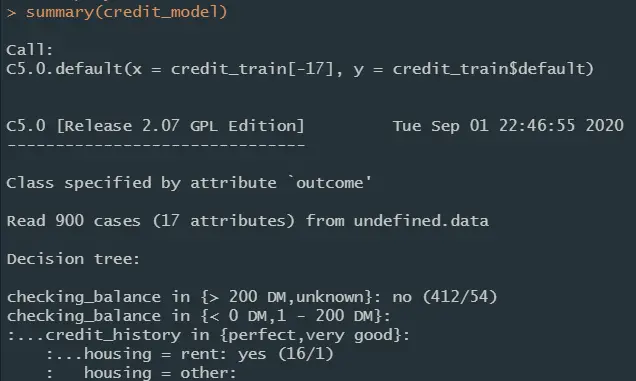
决策树的结构

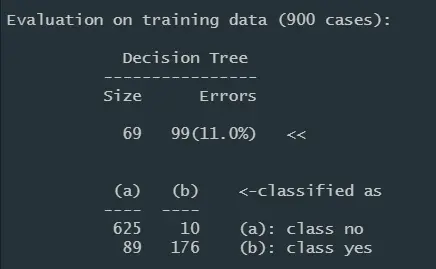
决策树生成的混淆矩阵

2.4）评估模型性能

依然使用混淆矩阵来评价模型。

## Step 4: Evaluating model performance ----
# create a factor vector of predictions on test data
credit_pred <- predict(credit_model, credit_test)

# cross tabulation of predicted versus actual classes
library(gmodels)
CrossTable(credit_test$default, credit_pred,
           prop.chisq = FALSE, prop.c = FALSE, prop.r = FALSE,
           dnn = c('actual default', 'predicted default'))
1
2
3
4
5
6
7
8
9

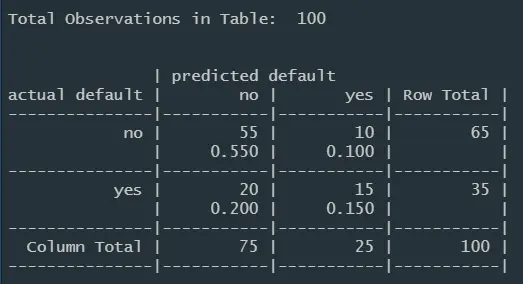
image.png

错误率30%，且只正确预测了15个贷款违约者。需要提升性能。

2.5）提高模型性能

通过自适应增强算法（boosting）

• 通过将很多学习能力弱的学习算法组合在一起，尤其使用优点和缺点的多种学习方法组合，可以显著提高分类器的准确性。

• 参数trials设为10，即10个试验（研究表明能降低约25%的错误率）

  Step 5: Improving model performance ----

  Boosting the accuracy of decision trees

  boosted decision tree with 10 trials

  credit_boost10 <- C5.0(credit_train[-17], credit_train$default,
  trials = 10)
  credit_boost10
  summary(credit_boost10)

  credit_boost_pred10 <- predict(credit_boost10, credit_test)
  CrossTable(credit_test$default, credit_boost_pred10,
  prop.chisq = FALSE, prop.c = FALSE, prop.r = FALSE,
  dnn = c(‘actual default’, ‘predicted default’))

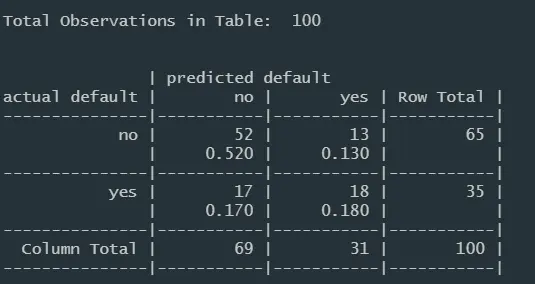
image.png

总的错误率仍为30%。缺乏更大的提高可能是本身使用了一个相对较小的训练集。

将惩罚因子分配到不同类型的错误上

假阴性付出的代价比较大（给有违约的申请者放贷），可以通过拒绝大量处于边界线的申请者来规避风险。

将惩罚因子设定在一个代价矩阵中，用来指定每种错误相对于其他任何错误有多少倍的严重性。如错放一个贷款违约者的损失是错失一次基于损失的4倍：

# create dimensions for a cost matrix
matrix_dimensions <- list(c("no", "yes"), c("no", "yes"))
names(matrix_dimensions) <- c("predicted", "actual")
matrix_dimensions

# build the matrix
error_cost <- matrix(c(0, 1, 4, 0), nrow = 2, dimnames = matrix_dimensions)
error_cost
1
2
3
4
5
6
7
8

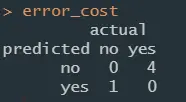
image.png

可通过costs参数来指定代价矩阵：

# apply the cost matrix to the tree
credit_cost <- C5.0(credit_train[-17], credit_train$default,
                          costs = error_cost)
credit_cost_pred <- predict(credit_cost, credit_test)

CrossTable(credit_test$default, credit_cost_pred,
           prop.chisq = FALSE, prop.c = FALSE, prop.r = FALSE,
           dnn = c('actual default', 'predicted default'))
1
2
3
4
5
6
7
8

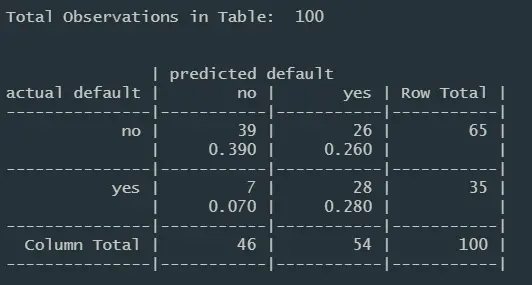
image.png

虽然总的错误率增加到了33%，但假阴性率降低到了7%。以增加错误肯定为代价，减少错误否定的这种折中的方案是可以接受的。

---