RCL-Learning:基于ResNet和卷积长短期记忆的时空空气污染物浓度预测模型_深度学习预测pm2.5浓度

A B S T R A C T

大气污染物浓度预测是预防污染事件发生的有效方法，为空气中有害物质提供预警。准确预测大气污染物浓度可以更有效地控制和预防大气污染。本研究采用大数据关联原理和深度学习技术建立PM2.5浓度预测模型。该模型包括基于残差神经网络(ResNet)的深度学习网络模型和基于卷积长短期记忆(ConvLSTM)的深度学习网络模型。利用ResNet深度提取多个城市污染物浓度的空间分布特征和气象数据。将输出作为ConvLSTM的输入，进一步提取从ResNet中提取的初步空间分布特征，同时提取污染物浓度和气象数据的时空特征。该模型将这两个特征结合起来，实现特征序列的时空相关性，从而准确预测目标城市未来一段时间内的PM2.5浓度。与其他神经网络模型和传统模型相比，所提出的污染物浓度预测模型提高了污染物浓度预测的准确性。对于1 ~ 3小时的预测任务，所提出的污染物浓度预测模型表现良好，均方根误差(RMSE)在5.478 ~ 13.622之间。此外，我们在目标城市进行了多尺度预测，取得了令人满意的效果，即使在1- 15小时的预测任务中，平均RMSE值也能达到22.927。

1. Introduction

PM2.5浓度预测可以看作是一个时间序列处理问题，可以根据过去的历史相关数据进行预测，例如湿度和温度等气象因素，以及SO2和CO等其他污染物因素。因此，必须提取和学习这些复杂相互作用关系之间的特征，以便进一步进行大气污染物的预测。此外，大气污染是一个区域扩散问题，需要考虑空间维度。这意味着邻近城市之间存在空间相关性的空气污染影响。大多数数值预测模型包括基于假设理论和先验知识的确定性模型;只将投入和产出视为独立过程的经验模型;数理统计模型;或使用小样本数据的传统机器学习模型。这些模型的主要优点是计算复杂度低、计算速度快、易于实现。然而，传统的数值分析模型在处理多城市站点的海量时空数据进行空间相关性大气污染物浓度预测时，遇到了三个问题:(1)需要提取和学习气象数据与大气污染数据之间复杂的相关性特征，以便进一步预测和改进性能;(2)准确提取历史数据间的时间相关性特征进行预测。这意味着在预测中应该忽略过去较长时间间隔的冗余信息或特征，而在一定时间内考虑有用的信息或特征，以改进预测;(3)基于区域内相邻城市的海量气象数据和污染数据，利用时间序列标签提取城市间的空间相关特征。这些问题导致大多数传统的空气污染物预测模型表现不佳。  

    鉴于此，我们提出了两种人工神经网络来构建我们的预测模型:残差神经网络(ResNet)和卷积长短期记忆网络(ConvLSTM)。理由如下:

   (1)深度网络，如卷积神经网络(CNN)，可以提取和学习NLP和计算机视觉领域的空间相关特征。然而，随着网络层深度的增加，梯度消失和网络退化问题加剧。因此，我们引入ResNet框架来提取数据的空间相关特征，避免了这两个问题。随着层数的增加，网络的性能将会提高 。同样，本文提出的污染物预测方法充分考虑了多城市污染物和气象数据的预测问题，利用深度残差神经网络(ResNet)的优势提取多城市污染物和气象数据之间输入的空间特征。

(2)提出卷积LSTM (ConvLSTM)，结合空间卷积运算提取时间序列特征，旨在从高维数据中学习时空关联特征。与递归神经网络(RNN)模型相比，ConvLSTM不仅可以避免梯度爆炸和消失问题，还可以解决高维数据的时空特征关联问题等。因此，我们可以利用卷积LSTM的优势，对ResNet提取的高维空间特征进行更深层次的时空相关特征提取。

  在本研究中，我们提出了一种集成了ResNet和ConvLSTM的端到端深度学习模型——rcllearning。本工作的主要贡献如下:

(1)利用ResNet作为提出的RCL-Learning模型的基础，避免了梯度消失或梯度爆炸的问题，可以从多个城市的污染物和气象数据中提取空间相关特征，同时也消除了深度网络的退化问题。

(2)模型采用ConvLSTM作为输出预测层，既获得了ConvLSTM预测时间序列的性能优势，又避免了梯度消失的问题，从而从残差网络层提取出隐藏在高维数据输出中的高级相关特征，实现挖掘数据时空相关性的目标;

(3)提出的RCL-Learning模型可以同时应用多个城市的气象和污染数据进行大数据环境监测，考虑数据的时空分布变化和规律，实现目标城市大气污染物浓度预测。在数据集上的实验表明，我们的框架比其他最先进的方法取得了更好的结果。

2. Related work

根据相关研究中所采用的预测方法的特点，大气污染物浓度预测从根本上可分为两大研究方法:确定性方法和统计方法。

  确定性方法可以应用于有限的历史数据集。然而，需要利用气象原理和统计方法来模拟基于大气物理和化学反应的污染物的实时排放、扩散、转化和去除过程。基于确定性方法的模型结构是在一定的理论假设和先验知识的基础上预先确定的。基于确定性方法的空气污染物浓度预测有几种常用方法:带扩展的综合空气质量模型(CAMs)、WRFChem模型、嵌套空气质量预测建模系统(NAQPMS)和社区多尺度空气质量模型(CMAQ)。

统计方法可以避免使用复杂的理论模型。与确定性方法相比，它们可以确定复杂污染物浓度数据之间的相关性，从而显示出较好的预测性能。在统计学的基础上，这两个分支可以扩展为传统的机器学习方法和新的深度学习方法。传统的机器学习方法包括支持向量机(SVM)、基于贝叶斯网络的多标签分类器、支持向量回归(SVR)方法、隐马尔可夫模型(HMM)等方法。

本文充分考虑预测模型对未来目标城市的PM2.5浓度进行更准确的预测，应实现以下目标:(1)有效利用多个城市的历史污染物浓度和气象大数据;(2)历史多城市污染物与气象数据时空相关性特征的深度挖掘。

3. Data description

3.1. Data collection

实验使用2014年5月13日至2018年5月30日收集的14个城市的历史污染物浓度和气象数据。本文的实验数据基于城市层面，即每个城市每小时的样本数据为一维特征向量，特征元素由污染物和气象因素组成。本文选取了以上海为中心的长三角地区经济快速发展的14个城市(上海、南京、苏州、南通、无锡、常州、镇江、杭州、宁波、绍兴、湖州、嘉兴、台州、舟山)作为城市选址。这些城市的地理位置离上海最近，污染物的扩散更容易相互影响。我们选取了空气质量指数(AQI)、PM2.5、PM10、SO2、NO2、O3、CO、温度、湿度、气压、风向、风速、云量、最高温度、最低温度和条件等16个污染物和气象因子。对于非数值气象因子，包括云和条件，我们执行一对一的数值映射。对于条件因子，我们将“mist”的值映射为1，“clear”的值映射为2，“cloudy”的值映射为3。空气污染物浓度和气象数据集的缺失值通过时空插值填充。图1显示了所有城市站点的位置。

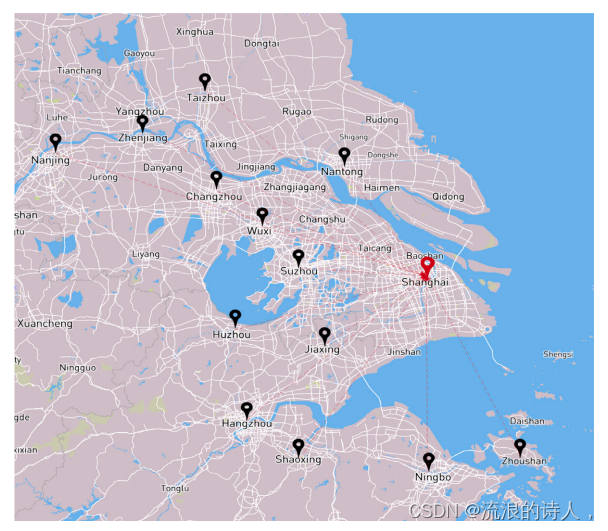
黑色圆圈表示周边城市，红色圆圈表示目标城市，箭头表示周边城市污染物对目标城市可能产生的影响。

 3.2. Particulate matter (PM2.5) and air quality index (AQI)

我们计算了训练集、验证集和测试集的AQI与空气污染物的相关系数，如表1所示。研究者提出PM2.5浓度可以用来评价空气质量。表1中，AQI与PM2.5的相关性最高，在训练集上相关系数值为0.993，在测试集上相关系数值高达0.997，这也印证了前人的研究结果。因此，本文选取与AQI相关性最高的PM2.5作为预测目标。

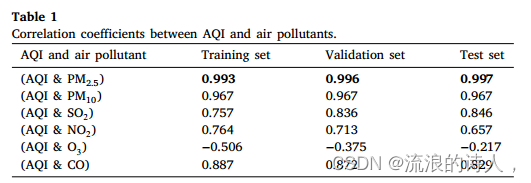
 3.3. The distribution characteristics of data

3.3.1. Analysis of temporal dimension

为探究污染物浓度分布特征与气象数据，选取目标城市上海2016年全年数据作为研究对象。图2为各污染物浓度(含空气质量指数)的年数值变化。观察PM2.5等污染物浓度的变化可以发现，污染物浓度变化的趋势总体上是一致的，这也反映了污染物之间可能存在着隐藏的关系。经统计分析，49.4%的2016年，PM2.5浓度大于WHO第一次临时标准35 μg∕m3，对部分异常敏感人群的健康影响较弱;2016年有13.7%的时间PM2.5浓度大于75 μg / m3，这将直接影响人们的日常出行和身体健康。因此，对于PM2.5的预测，一方面需要考虑PM2.5与其他污染物之间的隐性关系;另一方面也反映了准确的预测可以提前预防PM2.5对人体健康的影响。

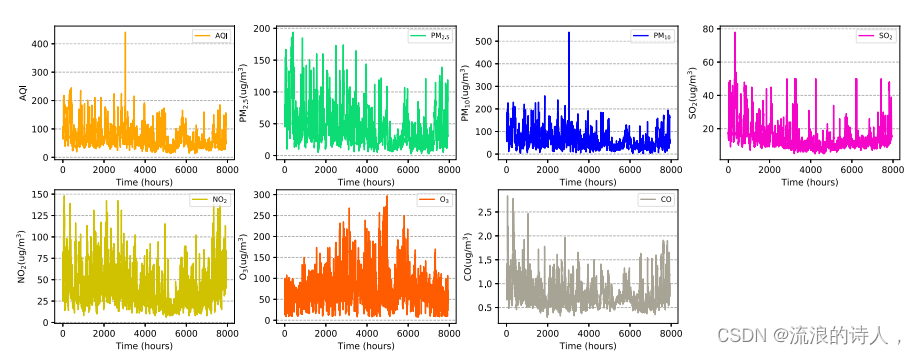
 图2所示。空气污染物浓度数据时间序列图

图3为气象因子的年数值变化。从图3可以看出，首先，温度、最高温度和最低温度的变化相同，气压的数值变化与温度正好相反;二是气象要素的数值类型和区间差异较大，但变化趋势高度相似，说明气象要素之间可能存在相互影响。例如，如图3所示，温度高可能导致气压低，反之亦然;三是气象因子与PM2.5浓度变化一致，说明大气污染物与气象因子之间存在隐性相关性。例如，在5000-6000 h之间，观测值有不同幅度的波动。因此，结合已有的研究成果，在PM2.5浓度预测研究中，我们将气象因子作为模型输入的一部分，提取污染物与气象因子之间的隐藏特征。

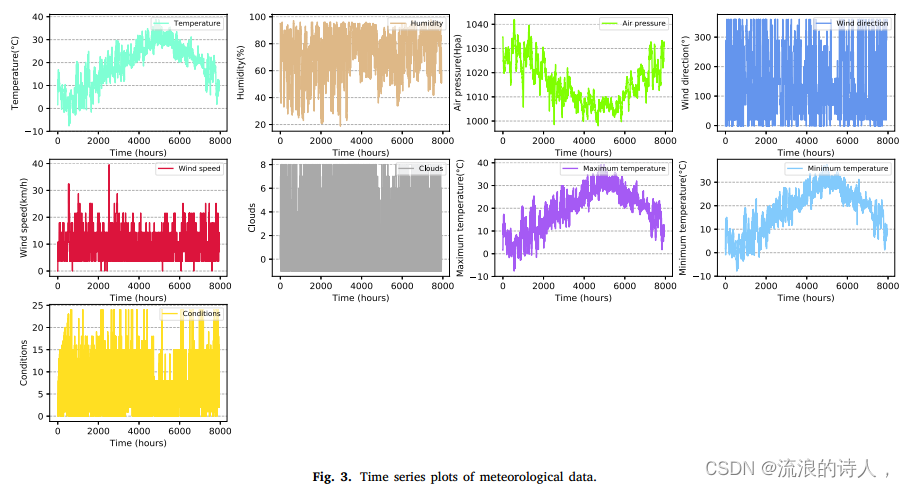
图3所示。气象资料的时间序列图。

 3.3.2. Analysis of spatial dimension

图2和图3中污染物和气象因子的数值变化是在时间维度上，我们做了详细的分析。上海作为目标城市，其PM2.5浓度在空间维度上也可能具有一定的特征。类似的选取2016年各城市PM2.5浓度数据。我们计算了上海与周边城市大气污染物的相关系数，如表2所示。结合表2和图1，首先，我们观察到离上海越近的城市关联度越高，我们在表格中用粗体表示，PM2.5的相关系数普遍高于PM10;其次，随着距离的增加，上海与周边城市大气污染物的相关系数逐渐减小。距离的影响表明，对于任何一个城市区域，除了预防局部污染物外，还需要协调区域污染物的预防，反映了空气污染物的空间相关性。接下来，图4显示了上海及周边城市PM2.5浓度的变化情况。首先，从图3和图4可以发现，各城市PM2.5浓度的一般规律是温度高时浓度低，温度低时浓度高。其次，在时空维度上，我们发现各城市PM2.5的变化格局在图4中是相似的。第三，通过对比上海与周边城市PM2.5浓度的变化，我们发现上海PM2.5浓度波动较大，且较为复杂。根据污染物的空间关联特征和上海及周边城市污染物浓度特征，这反映了考虑空间相关性的重要性。

3.4. Data division

 在我们的实验中，我们选择了70%的数据作为训练集，15%作为验证集，剩下的15%作为测试集。本研究中对数据进行划分的具体方法如下:首先，我们按照给定的窗口长度