图形排版[蓝桥杯]_蓝桥杯图形排版

题目描述

题目传送门

题意理解

对于一张图片，在某一行中我们可以有两个操作：
1.当该图片的宽度<=当前行的宽度， 我们将其放入当前行
2.当该图片的宽度>当前行的宽度，我们将图片进行压缩，并放入当前行。从下一张图片开始，另起一行

以下是基于题目给的图片规格进行排版，计算总高度的过程

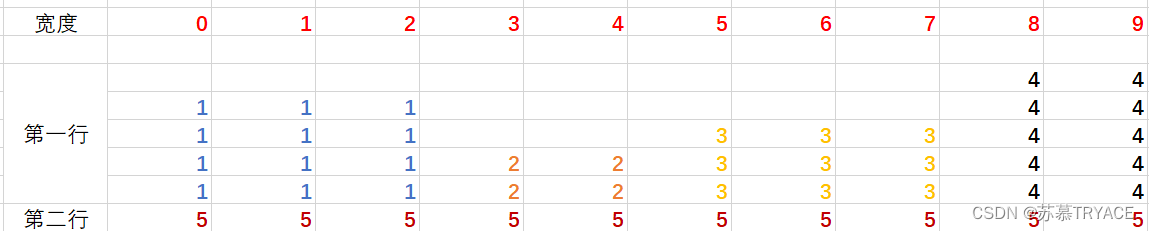
前三张图片可以顺次放在第一行，此时宽度剩下2
第四张图片规格较大，压缩后规格变为2 * 5，放在第一行
最终，第一行的高度为5

第五张图片开始，放在第二行
第五章图片规格较大， 进行压缩后为10 * 1，放在第二行
最终， 第二行的高度为1

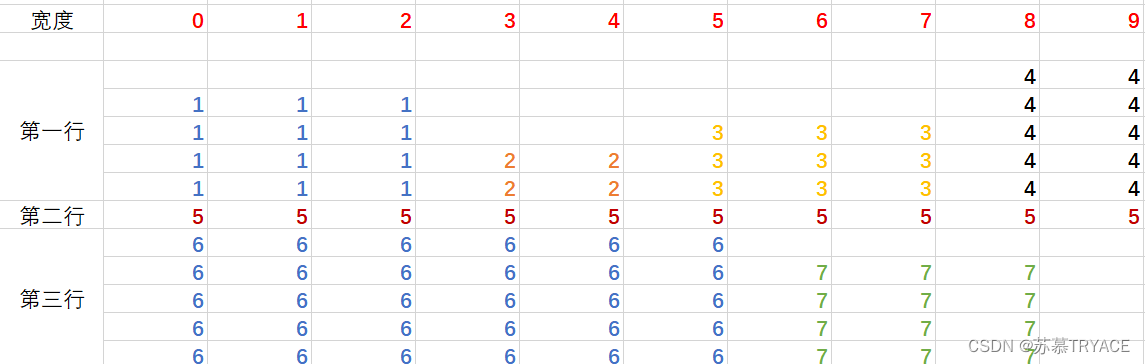
从第六张图片开始放在第三行
第六、七张图片可顺次放在第三行
最终， 第三行高度为5

至此所有图片全部排版完成，总高度为每一行的高度之和，即5 + 1 + 5 = 11

方法一：枚举（不能全部通过）

思路

模拟每一张图片被删除的情况，计算每一种情况的总高度，取最小值

代码

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef pair<int, int> PII;
vector<PII> g;
int n, m;
int solve(int x) //删掉下标为x的图片， 返回该情况下的高度
{
	int temp_m = m, height = 0, sum = 0;
	for(int i = 0; i < n; i ++)
	{
		if(i == x) continue; //模拟删掉下标为x的图片 
		if(temp_m > g[i].first) //当前行可以放开 
		{
			temp_m -= g[i].first;
			height = max(height, g[i].second); //更新最大高度 
		}
		else //当前行不可以放开 
		{
      int temp = ceil(g[i].second * 1.0 * temp_m / g[i].first); //缩放图片，缩放前后宽高比例不变
			height = max(height, temp);
			sum += height; //计算当前行的总高度 
			height = 0; //换行 
      temp_m = m;
		}
	}
	if(!height) sum += height;
	return sum; 
} 
int main()
{
	cin >> m >> n;
	for(int i = 0; i < n; i ++)
	{
		int w, h;
		cin >> w >> h;
		g.push_back({w, h});
	}
	int res = 0x3f3f3f3f;
	for(int i = 0; i < n; i ++) //模拟每一张图片被删掉的情况，取出其中的最小高度
	{
		res = min(res, solve(i));
	}
	cout << res << endl;
	return 0; 
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

时间复杂度:O(n²)

方法二：预处理

思路

来源：BV1GE411F7Pj

插入图片的过程中，一张或几张图片可以恰好填充一行（有些图片可能经过压缩），我们可以预处理来这样的结果，即以某一张图片为开端的图片的排版结果，这样当我们枚举过程中发现当前图片恰好可以填充一行，则后面的图片我们直接调用预处理的结果即可

AC代码

#include <iostream>
#include <cmath> 
#include <vector>
using namespace std;
const int N = 100010;
typedef pair<int, int> PII; //宽 高 
PII temp_Picture;
vector<PII> g;
int f[N]; //f[i]表示下标为i及其后面的图片另起一行插入得到的高度 
int n, m;
void Add_Row(PII &t, int idx) //将下标为idx的图片加入当前行 
{
	if(t.first + g[idx].first < m) //当前行可以顺次放下编号为idx的图片 
	{
		t.first += g[idx].first; //更新当前行的高度 
		t.second = max(t.second, g[idx].second);
	}
	else
	{
		int temp_h = ceil(g[idx].second * (m - t.first) * 1.0 / g[idx].first);
		t.second = max(t.second, temp_h);
		t.first = m;
	}
}
int Add_Picture(PII t, int idx) //将下标为i及其后面的图片加入当前行
{
	while(idx < n && t.first < m)
	{
		Add_Row(t, idx);
		idx ++;
	}
	return t.second + f[idx]; //这里可以解释为什么预处理要倒序，如果正序遍历，idx不断增大，但可能 f[idx]还未处理，即始终为0 
}
int main()
{
	cin >> m >> n;
	for(int i = 0; i < n; i ++) //存储每一张图片的信息 
	{
		int w, h;
		cin >> w >> h;
		g.push_back({w, h});
	} 
	
	for(int i = n - 1; i >= 0; i --) //预处理
	{
		temp_Picture = {0, 0}; //f[i]的含义是：标为i~n的图片另起一行插入得到的高度，因此我们每次操作都是居于"白纸"的情况排版 
		f[i] = Add_Picture(temp_Picture, i); 
	}
	
	int res = 0x3f3f3f3f, sum = 0; 
	temp_Picture = {0, 0};
	for(int i = 0; i < n; i ++) 
	{
		res = min(res, sum + Add_Picture(temp_Picture, i + 1)); //模拟删除编号为i的图片，这里会间接使用预处理的f数组 
		Add_Row(temp_Picture, i); //下次循环模拟不要编号为i + 1的图片，因此我们需要先将第i张图片放入"白纸"中 
		if(temp_Picture.first == m) //另起一行 
		{
			sum += temp_Picture.second;
			temp_Picture = {0, 0};
		} 
	} 
	cout << res << endl;
	return 0; 
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

欢迎大家批评指正！！！