降维算法：在单细胞转录组生信分析中，常见的降维算法有两种，UMAP(Uniform Manifold Approximation and Projection) 和T-SNE(t-distributed stochastic neighbor embedding)。UMPA 运算速度会更快，并且在保留数据结构的同时提供了更好的扩展性。

UMAP的主要步骤

学习高维空间中的流形结构
找到该流形的低维表示，优化低维图

1. 学习高维空间中数据点间的距离

UMAP首先使用Nearest-Neighbor-Descent算法来找到每个数据点的最近邻。这个过程可以通过调整UMAP的超参数n_neighbors来指定我们想要使用多少个近邻点。

影响因素：试验n_neighbors的数量是非常重要的，因为它会影响UMAP如何平衡数据的局部和全局结构。它通过限制局部邻域的大小来实现，在尝试学习流形结构时起到一定的调节作用。
n_neighbors的作用：小的n_neighbors值表示我们想要一个非常局部的解释，以准确捕捉数据结构的细节。而较大的n_neighbors值则意味着我们的估计将基于更大的区域，因此在整个流形中更广泛地准确

2. 构建高维图

UMAP假设数据点在流形上均匀分布，即它们之间的空间根据数据的密集程度而变化。涉及两个关键超参数local_connectivity和n_neighbors的作用：

local_connectivity参数

理解为下限：这个参数是用来控制每个数据点至少连接到另一个点的确定性程度。
默认值为1：意味着每个点都100%确定地连接到另一个点，也就是连接的数量的最低要求。

n_neighbors参数

理解为上限：这个参数控制一个点直接连接到其第几个邻居的可能性。
默认值为15：这表示一个点直接连接到它的第16个邻居的可能性为0%，因为在构建UMAP使用的邻域图时，它已经处在局部区域之外。例如2到15：这个范围表示点连接到其第2个到第15个邻居之间的确定性程度。它介于0%和100%之间，表示一定程度的确定性，但不是完全确定。

3. 构建低维图

从高维空间学习近似流形后，UMAP 的下一步将数据从高维空间投影到低维空间。

计算最小距离

在投影到低维空间时，UMAP希望保持流形上的距离与全局坐标系下的欧几里得距离相对应。

目标：不改变距离，而是希望流形上的距离在投影后仍然是在全局坐标系下的标准欧几里得距离。

min_dist超参数

为了实现这一目标，UMAP引入了一个名为min_dist（默认值为0.1）的超参数，用于定义低维嵌入点之间的最小距离。通过这个参数，可以控制投影到低维空间后点的最小分布，以避免低维嵌入中许多点相互重叠的情况。

最小化成本函数

在指定了最小距离后，UMAP算法开始寻找更好的低维流形表示。为了实现这一目标，UMAP通过最小化特定的成本函数（也称为交叉熵）来进行投影。

成本函数：通过最小化这个成本函数，UMAP寻找边的最优权值，这些权值决定了在低维表示中的点之间的连接。

优化过程：这个过程可以通过随机梯度下降法来进行优化。随机梯度下降法是一种优化方法，用于找到使成本函数最小化的参数值，即在这里是寻找使得低维表示最符合原始高维数据结构的参数。

R语言中的RunUMAP函数


RunUMAP(object, ...)
 
## Default S3 method:
RunUMAP(
object,
reduction.key = "UMAP_",
assay = NULL,
reduction.model = NULL,
return.model = FALSE,
umap.method = "uwot",
n.neighbors = 30L,
n.components = 2L,
metric = "cosine",
n.epochs = NULL,
learning.rate = 1,
min.dist = 0.3,
spread = 1,
set.op.mix.ratio = 1,
local.connectivity = 1L,
repulsion.strength = 1,
negative.sample.rate = 5,
a = NULL,
b = NULL,
uwot.sgd = FALSE,
seed.use = 42,
metric.kwds = NULL,
angular.rp.forest = FALSE,
verbose = TRUE,
...
)

### 参数说明：

- object：一个物体
- ...：传递给其他方法和UMAP的参数

- reduction.key：维度缩减键，指定维度名称的数字之前的字符串。默认为UMAP

- assay：提取数据的分析，或者用于在图形上运行UMAP构建图形的分析

- reduction.model：包含UMAP模型的DimReduc对象

- return.model：UMAP是否返回uwot模型

- umap.method：要运行的UMAP实现。
  - "uwot"：运行UMAP通过uwot R包
  - "uwot-learn"：运行UMAP通过uwot R包并返回学习的UMAP模型
  - "umap-learn"：运行python umap学习包的Seurat包装器

- n.neighbors：局部近似流形结构中使用的相邻点的数量。一般应在5到50之间。

- n.components：要嵌入的空间的尺寸。

- metric：度量，用于衡量输入空间中的距离。

- n.epochs：用于优化低维嵌入的训练次数。根据数据集大小选择一个值（大数据集为200，小数据集为500）。

- learning.rate：嵌入优化的初始学习率。

- min.dist：控制允许嵌入压缩点的程度。默认0.3，越小则每个cluster越聚集。合理的值在 0.001 到 0.5 的范围内，0.1 是合理的默认值。

- spread：嵌入点的有效比例。

- set.op.mix.ratio：插值作为集合运算的参数，用于组合局部fuzzy单形集以获得全局fuzzy单形集。

- local.connectivity：本地连接性，即应假定在本地级别连接的最近邻居的数量。

- repulsion.strength：负样本的加权。

- negative.sample.rate：每个阳性样本要选择的阴性样本数。

- a：用于控制嵌入的参数。

- b：用于控制嵌入的参数。

- uwot.sgd：设置uwot：：umap。

- seed.use：设置随机种子，默认为42。

- metric.kwds：传递给度量的参数字典。

- angular.rp.forest：是否使用角度随机投影林来初始化近似最近邻搜索。

- verbose：控制冗长输出。

- dims：用作输入特征的维度。

- reduction：用于UMAP输入的降维方法，默认为PCA。

- features：在特征子集上运行UMAP（而不是在缩减的维度集上运行）。

- graph：要在其上运行UMAP的图形的名称。

- nn.name：运行UMAP的knn输出的名称。

- slot：用于提取数据的插槽，默认为数据槽。

- reduction.name：在Seurat对象中存储维度缩减的名称。

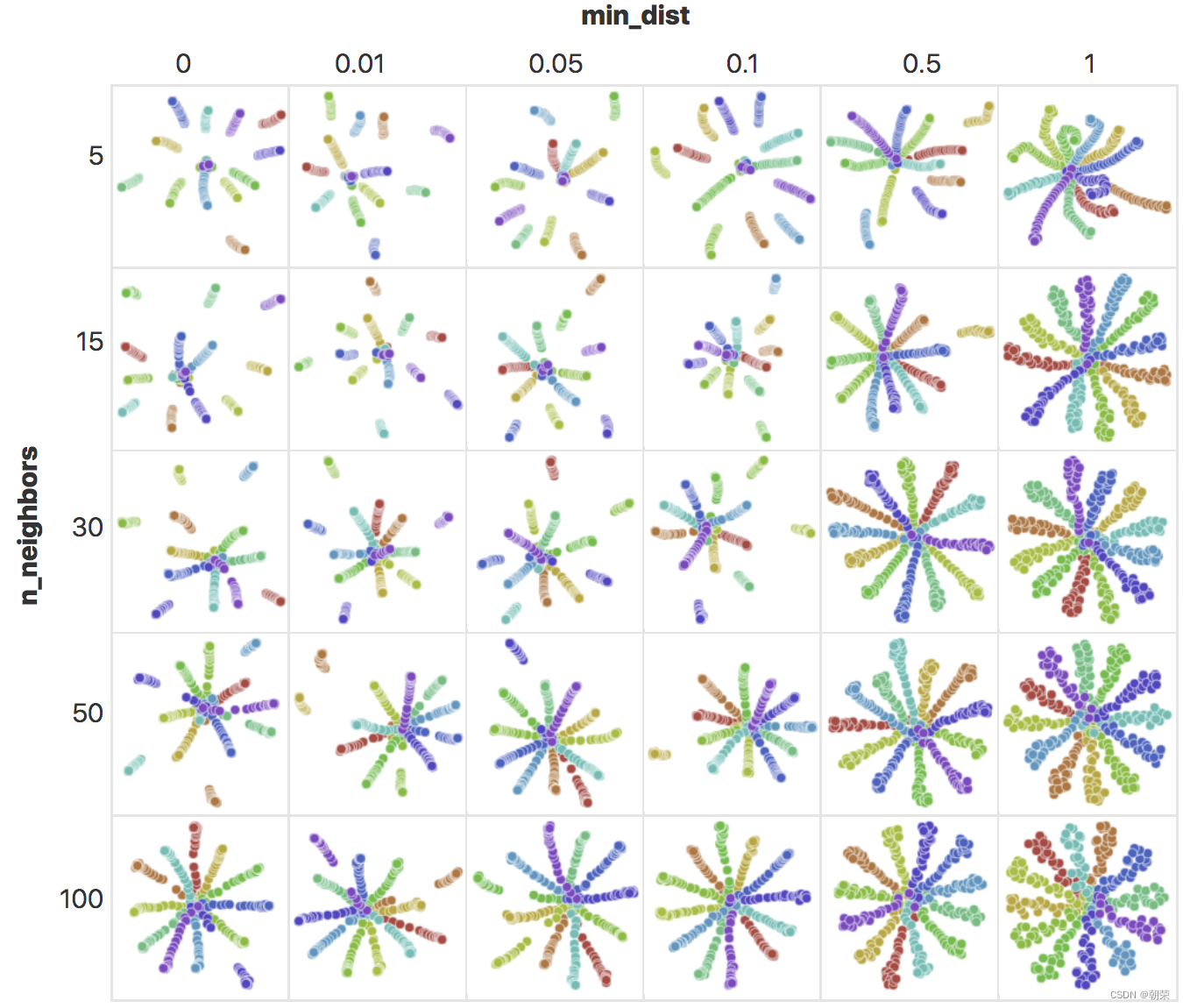
不同min_dist参数和n_neighbors参数的效果图

关键参数

object：

含义：要进行降维的Seurat对象或矩阵。
类型：Seurat对象或矩阵。

dims：

含义：要使用的维度数。
类型：整数向量。
默认值：NULL，表示使用所有维度。

n_neighbors：

含义：在计算邻域时要考虑的最近邻居数目。
类型：整数。
默认值：15。

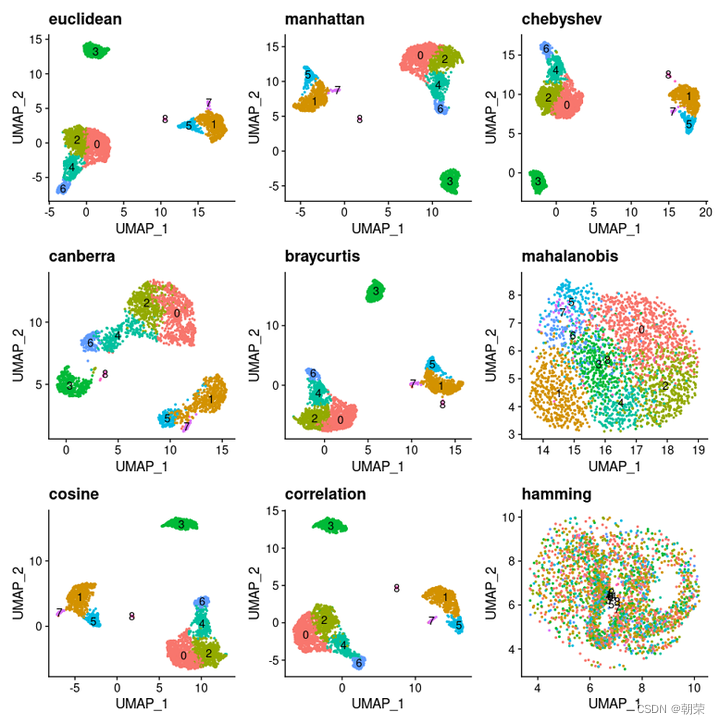
metric：

含义：计算距离的度量方法。
类型：字符串。
默认值："euclidean"。

min_dist：

含义：最小的距离。
类型：浮点数。
默认值：0.5。

spread：

含义：在高维空间中的分布。
类型：浮点数。
默认值：1.0。

n_components：

含义：输出的UMAP维度数。
类型：整数。
默认值：2。

Reference

[1] McInnes, L, Healy, J, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, ArXiv e-prints 1802.03426, 2018

[2] Kobak, D., Berens, P. The art of using t-SNE for single-cell transcriptomics. Nat Commun 10, 5416 (2019). https://doi.org/10.1038/s41467-019-13056-x

[3] A Guide to Analyzing Single-cell Datasets, John F. Ouyang, January 2023

http://www.idata8.com/rpackage/Seurat/RunUMAP.html

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/盐析白兔/article/detail/343705