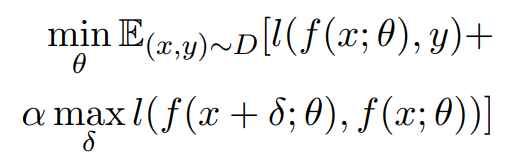【学习笔记】NLP的对抗训练总结_freelb:自然语言理解的对抗训练

对抗训练

在NLP数据竞赛中用到了对抗训练，颇有效果，总结了主要的几个对抗训练方法，其中用得比较多的还是FGM和PGD。

参考文章

https://www.spaces.ac.cn/archives/7234

https://wuwt.me/2020/11/06/adverisal-train-2020/

https://www.spaces.ac.cn/archives/6051

https://zhuanlan.zhihu.com/p/104040055

1. 基本概念

1.1 对抗样本

它首先出现在论文《Intriguing properties of neural networks》之中。简单来说，它是指对于人类来说“看起来”几乎一样、但对于模型来说预测结果却完全不一样的样本，比如下面的经典例子。

什么样的样本才是最好的对抗样本呢？对抗样本一般需要具备两个特点：

• 相对于原始输入，所添加的扰动是微小的；
• 能使模型犯错。

1.2 对抗攻击

想办法造出更多的对抗样本。

1.3 对抗防御

想办法让模型能正确识别更多的对抗样本。

1.4 对抗训练

所谓对抗训练，则是属于对抗防御的一种，它构造了一些对抗样本加入到原数据集中，希望增强模型对对抗样本的鲁棒性；同时，在NLP中它通常还能提高模型的表现，因此，NLP中的对抗训练更多是作为一种正则化手段来提高模型的泛化能力。

对抗训练的假设是：给输入加上扰动后，输出分布和原Y的分布一样。

2. Min-Max

2.1 核心公式

总的来说，对抗训练可以统一写成如下格式：

其中，$D$代表训练集，$x$代表输入，$y$代表标签，$\theta$是模型参数，$L(x,y;\theta )$是单个样本的loss，$\Delta x$是对抗扰动，$\Omega$是扰动空间。这个统一的格式首先由论文《Towards Deep Learning Models Resistant to Adversarial Attacks》提出。

该公式分为两部分，一个是内部损失函数的最大化，一个是外部经验风险的最小化。

• 内部max是为了找到worst-case的扰动，也就是攻击。
• 外部min是为了基于该攻击方式，找到最鲁棒的模型参数，也就是防御，其中D是输入样本的分布。

2.2 分步理解

这个式子可以分步理解如下：

1、往输入$x$里边注入扰动$\Delta x$，$\Delta x$的目标是让$L(x+\Delta x,y;\theta )$越大越好，也就是说尽可能让现有模型的预测出错；

2、当然$\Delta x$也不是无约束的，它不能太大，否则达不到“看起来几乎一样”的效果，所以$\Delta x$要满足一定的约束，常规的约束是$\Vert \Delta x\Vert \le ϵ$，其中$ϵ$是一个常数；

3、每个样本都构造出对抗样本$x+\Delta x$之后，用$(x+\Delta x,y)$作为数据对去最小化loss来更新参数$\theta$（梯度下降）；

4、反复交替执行1、2、3步。

2.3 和GAN的区别

由此观之，整个优化过程是max和min交替执行，这确实跟GAN很相似，不同的是，GAN所max的自变量也是模型的参数，而这里max的自变量则是输入（的扰动），（这应该是和对抗训练和GAN最本质的区别。），也就是说要对每一个输入都定制一步max。

3. NLP中的对抗训练思路

3.1 核心总结

核心用一句话总结：用一句话形容NLP中对抗训练的思路，就是在输入上进行梯度上升（增大loss），在参数上进行梯度下降（减小loss）。 由于输入会进行embedding lookup，所以实际的做法是在embedding table进行梯度上升。（既然负梯度是Loss下降最快的方向，那么正梯度就是Loss上升最快的方向。）

3.2 CV任务中的对抗扰动

首先，CV任务的输入是连续的RGB值，因此可以直接在原始图像上添加扰动。对于CV任务来说，一般输入张量的shape是(b,h,w,c)，这时候我们需要固定模型的batch size（即b），然后给原始输入加上一个shape同样为(b,h,w,c)、全零初始化的Variable，比如就叫做$\Delta x$，那么我们可以直接求loss对x的梯度，然后根据梯度给$\Delta x$赋值，来实现对输入的干扰，完成干扰之后再执行常规的梯度下降。

3.3 原始文本扰动和Embedding扰动带来的问题

而NLP问题中，输入是离散的单词序列，一般以one-hot vector的形式呈现，如果直接在raw text上进行扰动，那么扰动的大小和方向可能都没什么意义。

Goodfellow在17年的ICLR中提出了可以在连续的embedding上做了扰动。然而，对比图像领域中直接在原始输入加扰动的做法，在embedding上加扰动会带来一个问题：这个被构造出来的“对抗样本”并不能对应到某个单词上，即，扰动后的Embedding向量不一定能匹配上原来的Embedding向量表，这样一来对Embedding层的扰动就无法对应上真实的文本输入，这就不是真正意义上的对抗样本了，因为对抗样本应该要能对应一个合理的原始输入。因此，反过来在inference的时候，对手也没有办法通过修改原始输入得到这样的对抗样本。

3.4 Embedding扰动仍然有效—一种正则化手段

然而，实验结果显示，在很多任务中，在Embedding层进行对抗扰动能有效提高模型的性能，所以仍然是非常有意义的。在CV任务中，根据经验性的结论，对抗训练往往使得模型在非对抗样本上表现变差，然而神奇的是，在NLP任务中，模型的泛化能力反而变强了。因此，在NLP任务中，对抗训练的角色不再是为了防御基于梯度的恶意攻击，反而更多的是作为一种正则化，提高模型的泛化能力。

3.5 对Embedding参数矩阵进行扰动

对于NLP任务来说，原则上也要对Embedding层的输出进行同样的操作，Embedding层的输出shape为(b,n,d)，所以也要在Embedding层的输出加上一个shape为(b,n,d)的Variable，然后进行上述步骤。但这样一来，我们需要拆解、重构模型，对使用者不够友好。

不过，我们可以退而求其次。Embedding层的输出是直接取自于Embedding参数矩阵的，因此我们可以直接对Embedding参数矩阵进行扰动，即对Embedding Table进行梯度上升。这样得到的对抗样本的多样性会少一些（因为不同样本的同一个token共用了相同的扰动），但仍然能起到正则化的作用，而且这样实现起来容易得多。

笔者个人的理解：这里有两点，

1. 首先肯定不能对原始输入的文本进行扰动，所以我们对词嵌入层进行扰动，词嵌入层其实也相当于后面深层网络的初始输入，所以也算是对输入进行扰动。所以，我们直接对整体的词嵌入矩阵进行扰动，因为嵌入层的输入是lookup table的过程。
2. 另外，这样不用再对每个输入都定制一个Max的过程，因为不同样本的同一个token共用了相同的扰动。

4. 主要方法介绍

4.1 FGSM(Fast Gradient Sign Method),ICLR 2015

4.1.1 原理

假设对于输入的梯度为：

$$g={\nabla }_{x}L(\theta ,x,y)$$

那扰动肯定是沿着梯度的方向往损失函数的极大值走：

$$r_{adv}=ϵ\cdot sign(g)$$

sign(x)是符号函数，即x大于0的时候是1，小于0的时候是-1，等于0的时候是0。

这里和FGM的主要区别在于，FGSM每个方向都走相同的一步。

4.1.2 Pytorch实现

import torch
import torch.nn as nn
import torch.nn.functional as F
 
 
# FGSM
class FGSM:
    def __init__(self, model: nn.Module, eps=0.1):
        #等号右边应该是一个括号，并把括号里面的这个唯一的值赋给model
        #注意：等号右边不是只包含一个元素的元组，如果是只包含一个元素的
        #元组，应该这样写：(123,),这时赋值时，左边的变量也为一个只包含
        #一个元素的元组
        self.model = (
            model.module if hasattr(model, "module") else model
        )
        self.eps = eps
        self.backup = {}
 
    # only attack word embedding
    def attack(self, emb_name='embedding'):
        for name, param in self.model.named_parameters():
 
            if param.requires_grad and emb_name in name:
                self.backup[name] = param.data.clone()
                r_at = self.eps * param.grad.sign()
                param.data.add_(r_at)
 
    def restore(self, emb_name='embedding'):
        for name, para in self.model.named_parameters():
            if para.requires_grad and emb_name in name:
                assert name in self.backup
                para.data = self.backup[name]
 
        self.backup = {}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

4.2 FGM(Fast Gradient Method),ICLR 2017

4.2.1 原理

更改了计算扰动的方式：

$$r_{adv}=ϵ\cdot (g/||g|{|}_2)$$

4.2.2 注意事项

• 注意在训练过程中epsilon不宜选取的过大或过小，设置过大会使得模型难以收敛，设置过小比如设置为0的话相当于单个样本训练两次。

• FGSM和FGM的区别在于采用的归一化方法不同，FGSM是通过Sign函数对梯度采取Max归一化，FGM则采用了L2归一化，理论上L2归一化更严格地保留了梯度的方向，因为Max归一化不一定和原始梯度的方向相同。

• 两种方法都有个假设，就是损失函数是线性的或者至少是局部线性的。如果不是（局部）线性的，那梯度提升的方向就不一定是最优方向了。

4.2.3 Pytorch实现

需要注意的是：这里的norm计算的是，每个样本的输入序列中出现过的词组成的矩阵的梯度norm。为了实现插件式的调用，笔者将一个batch抽象成一个样本，一个batch统一用一个norm，由于本来norm也只是一个scale的作用，影响不大。笔者的实现如下：

import torch
class FGM():
    def __init__(self, model):
        self.model = model
        self.backup = {}

    def attack(self, epsilon=1., emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                # tensor.clone()会创建一个与被clone的tensor完全一样的tensor，两者不共享内存但是新tensor仍保存在计算图中，即新的tensor仍会被autograd追踪
                # 这里是在备份
                self.backup[name] = param.data.clone()
                # 归一化
                norm = torch.norm(param.grad)
                if norm != 0 and not torch.isnan(norm):
                    r_at = epsilon * param.grad / norm
                    param.data.add_(r_at)

    def restore(self, emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.backup
                param.data = self.backup[name]
        self.backup = {}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

要使用对抗训练时，只需要添加几行代码：

# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    loss.backward() # 反向传播，得到正常的grad
    # 对抗训练
    # 在embedding上添加对抗扰动
    fgm.attack() 
    loss_adv = model(batch_input, batch_label)
    # 反向传播，并在正常的grad基础上，累加对抗训练的梯度，如果不想累加就加个梯度清零
    loss_adv.backward() 
    # 恢复embedding参数
    fgm.restore() 
    # 梯度下降，更新参数
    optimizer.step()
    model.zero_grad()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

4.3 PGD(Projected Gradient Descent),ICLR 2018

4.3.1 原理

内部max的过程，本质上是一个非凹的约束优化问题，FGM解决的思路其实就是梯度上升，那么FGM简单粗暴的“一步到位”，是不是有可能并不能走到约束内的最优点呢？当然是有可能的。

于是，一个很intuitive的改进诞生了：Madry在18年的ICLR中，提出了用Projected Gradient Descent（PGD）的方法，简单的说，就是 “小步走，多走几步”，如果走出了扰动半径为$ϵ$的空间，就映射回“球面”上，以保证扰动不要过大。PGD是一种迭代攻击，相比于普通的FGSM和FGM仅做一次迭代，PGD是做多次迭代，每次走一小步，每次迭代都会将扰动投射到规定范围内。

具体公式如下，其中，t指迭代次数。t+1时刻输入根据t时刻的输入及t时刻的梯度求出。${\prod }_{x+S}$的意思是，如果扰动超过一定的范围，就要映射回规定的范围S内，这里的x为原始的正常的样本输入值。

4.3.2 Pytorch实现

PGD基于FGM进行了改进，相较于FGM简单粗暴的每次都添加$ϵ$大小控制的干扰，PGD的干扰就以一种更为精细的方式生成。

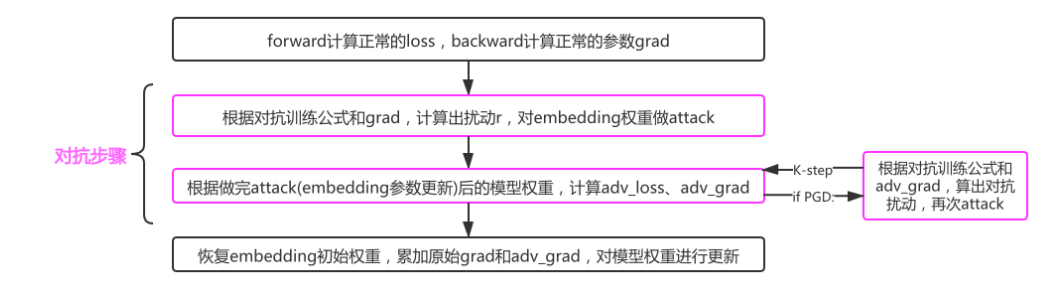
具体来说，针对每个训练样本，PGD第一步的操作是备份原来的梯度信息。然后，PGD进行K次对嵌入层添加干扰操作，即attack操作，并在第一次attck时备份嵌入层的权重参数。

在进行添加干扰之后，PGD相较于FGM还有额外的梯度操作，在前K-1次需要清空梯度，在最后第K次需要恢复一开始备份的原来的梯度信息。这样操作是因为前K-1次反向传播的目的是为下一次扰动的计算提供新的梯度，最后一次反向传播的作用是在原梯度基础上累加对抗训练的梯度，模型最终的梯度就是最开始的梯度加上最后一次扰动产生的梯度。在完成了K次attack操作并将最后一次attack产生的梯度累加到原来的梯度之后，模型还需要恢复原来的嵌入层参数。

伪代码如下：

对于每个样本x:
  (1).计算x的前向loss、反向传播得到梯度并备份
  对于每步t:
    (2).根据embedding矩阵的梯度计算出扰动r，并加到当前embedding上，相当于x+r(超出范围则投影回epsilon内)
    (3).if t不是最后一步: 将梯度归0，根据(1)的x+r计算前后向并得到梯度
    (4).if t是最后一步: 恢复(1)的梯度，计算最后的x+r并将梯度累加到(1)上
  (5).将embedding恢复为(1)时的值
  (6).根据(4)的梯度对参数进行更新
1
2
3
4
5
6
7
8

import torch
class PGD():
    def __init__(self, model):
        self.model = model
        self.emb_backup = {}
        self.grad_backup = {}

    def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
            # 备份embedding    
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0 and not torch.isnan(norm):
                    r_at = alpha * param.grad / norm
                    # 每次扰动都进行叠加了
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data, epsilon)

    def restore(self, emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}

    def project(self, param_name, param_data, epsilon):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > epsilon:
            # 映射回球面，向量单位化，然后乘半径epsilon
            r = epsilon * r / torch.norm(r)
        return self.emb_backup[param_name] + r

    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                self.grad_backup[name] = param.grad.clone()

    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                param.grad = self.grad_backup[name]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

训练时，通过如下代码调用：

pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    # 反向传播，得到正常的grad
    loss.backward() 
    # 备份梯度
    pgd.backup_grad()
    # 对抗训练
    for t in range(K):
        # 在embedding上添加扰动, first attack时备份param.data
        # t+1时刻输入根据t时刻的输入及t时刻的梯度求出，这里多步迭代体现在这里
        # t时刻的输入，即t时刻的x+r，并没有被清空（没恢复，pgd.restore()），所以扰动是不断叠加的。
        pgd.attack(is_first_attack=(t==0)) 
        if t != K-1:
            model.zero_grad()
        else:
            pgd.restore_grad()
        # 计算损失，反向传播，如果是最后一步，在正常的grad基础上，累加对抗训练的梯度
        loss_adv = model(batch_input, batch_label)
        # 反向传播，这里有t时刻的输入，在其清空之前，拿去求扰动
        loss_adv.backward() 
    # 恢复embedding参数
    pgd.restore() 
    # 更新参数
    optimizer.step()
    model.zero_grad()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

4.3.3 分析

可以看到，在循环中扰动r是逐渐累加的，要注意的是最后更新参数只使用x+最后一个扰动r算出来的梯度。

PGD的优点：

• 由于每次只走很小的一步，所以局部线性假设基本成立的。经过多步之后就可以达到最优解了，也就是达到最强的攻击效果。
• 论文还证明用PGD算法得到的攻击样本，是一阶对抗样本中最强的了。这里所说的一阶对抗样本是指依据一阶梯度的对抗样本。
• 如果模型对PGD产生的样本鲁棒，那基本上就对所有的一阶对抗样本都鲁棒。
• 实验也证明，利用PGD算法进行对抗训练的模型确实具有很好的鲁棒性。

PGD的缺点：

• PGD虽然简单，也很有效，但是存在一个问题是计算效率不高。不采用对抗训练的方法m次迭代只会有m次梯度的计算，但是对于PGD而言，每做一次梯度下降（获取模型参数的梯度，训练模型），都要对应有K步的梯度提升（获取输入的梯度，寻找扰动)。所以相比不采用对抗训练的方法，PGD需要做m(K+1)次梯度计算。

  这里个人理解是，每更新一次模型参数，要先一次梯度下降备份参数，提供初始梯度，然后进行K次梯度提升，这K次梯度提升其实就是通过K次loss.backward()计算得到梯度然后进行扰动的计算，所以总共K+1次的梯度计算。

4.4 FreeAT(Free Adversarial Training),NIPS 2019

4.4.1 改进动机

普通的 PGD方法，在计算一个epoch的一个batch时：

• 内层循环经过K次前向后向的传播，得到K个关于输入的梯度，更新扰动；
• 外层循环经过1次前后向的传播得到关于参数的梯度更新网络。

这样的计算成本是十分高昂的，其实，我们在针对输入或参数中的一个计算梯度时，能够几乎无成本的得到另外一个的梯度。这就是 Free Adversarial Training的思想，在一次计算中利用更多的信息加速对抗性学习的训练。

在PGD的计算过程中，每次做前向后向计算时，不管是参数的梯度还是输入的梯度，都会计算出来，只不过在梯度下降的过程中只利用参数的梯度，在梯度提升的过程中只利用**输入的梯度，**这实际上有很大的浪费。 我们能不能在一次前向后向计算过程中，把计算出来的参数的梯度和输入的梯度同时利用上？这就是FreeAT的核心思想。

4.4.2 算法

如何做呢？

• FreeAT仍然采用了PGD这种训练方式，但对于每个min-batch的样本，会求m次梯度，每次求得梯度，我们既用来更新扰动，也用来更新参数。原始的PGD训练方法，每次内层计算只用梯度来更新扰动，等m步走完之后，才重新再计算一次梯度，更新参数。
• FreeAT对每个样本进行连续重复的m次训练，为了保证总的梯度计算次数和普通训练的梯度次数一样，把原来的epoch除以m。
• 计算扰动时会复用上一步的梯度。
• 最终只需要$N_{ep}$次梯度计算

算法流程如下图所示：

4.5 YOPO(You can Only Propagate Once),NIPS 2019

4.5.1 改进动机

YOPO5 的出发点是利用神经网络的结构来降低梯度计算的计算量。从极大值原理PMP（Pontryagin’s maximum principle）出发，对抗扰动只和网络的第 0 层有关，即只在 embedding 层上添加扰动。再加之，层之间是解耦合的，那就不需要每次都计算完整的前后向传播。

极大值原理PMP(Pontryagin’s maximum principle)是optimizer的一种，它将神经网络看作动力学系统。这个方法的优点是在优化网络参数时，层之间是解耦的。通过这个思想，我们可以想到，既然扰动是加在embedding层的，为什么每次还要计算完整的前后向传播呢？

4.5.2 算法

基于这个想法，作者就想复用后面几层的梯度，减少非必要的完整传播。可以将 PGD 的r次攻击拆成 m×n次。

首先在m轮中，每轮只进行一次前向后向传播。每轮传播中，进行完整的前向传播，在接下来的反向传播中到第1层就停止，用p记录下反向传播的结果，把p固定住，认为它不会随着扰动的改变而改变；接着在第0层上进行n次攻击，这样YOPO只完成了m次的完整正向反向传播但却实现了m×n次扰动的更新。

这样只要计算对于网络第0层$f_0$的梯度，减少了正反向传播的层数，从而加快速度。

如上图所示，其中橄榄绿和黄色的块代表网络中间层的 $x_t$ ，橘红色的块代表每一层对于loss的梯度，也就是$p_t$。

左边是传统的PGD-r算法，可以看出，每要更新一次第0层的$\eta$，就需要完成一次完整的正向传播和反向传播，而PGD-r算法每迭代一次$\theta$都需要进行r次这样的更新。

右边是YOPO-m-n算法，同样是更新第0层的参数$\eta$ ，首先也同样需要进行$x_t$的正向传播，然后进行$p_t$的反向传播，不同的是在得到$p_1$之后，将它拷贝一份，利用$p_1$和函数$f_0$来计算的$\eta$梯度，并执行n次梯度下降，然后再进行下一次的正反向传播。这样一来，YOPO-m-n每进行一次完整的正反向传播，都可以完成$\eta$的n次更新。

4.6 FreeLB(Free Large Batch Adversarial Training),ICLR 2020

4.6.1 原理和算法

FreeLB针对PGD的多次迭代训练的问题进行了改进：

• PGD是迭代K次扰动后取最后一次扰动的梯度更新参数，FreeLB是取K次迭代中的平均梯度。具体而言，FreeLB每轮计算则不做model.zero_grad()，相当于每轮的 loss.backward()都在param.grad上做累加，最后取平均。
• PGD更精确、更谨慎、更符合梯度上升的一贯作风；FreeLB更粗放、更快。
• 这篇文章还提出了对抗训练和dropout不能同时使用。
• 最终需要进行$N_{ep}\ast K$次梯度计算

4.6.2 FreeLB和FreeAT、PGD的区别

• 和FreeAT一样，FreeLB也想更高效的利用两种梯度。但是和FreeAT不一样的是，FreeLB并不是在每次梯度提升的过程中，都会对参数进行更新，而是将参数的梯度累积起来。这样走过K步之后，FreeLB利用K步之后积累的参数梯度对参数θ进行更新。
• 根据算法源代码，PGD需要进行$N_{ep}\ast (K+1)$次梯度计算，FreeAT需要进行$N_{ep}$次，FreeLB需要$N_{ep}\ast K$次。虽然FreeLB在效率上并没有太大的优势，但是其效果不错。

这里PGD多的一次应该是指一开始的梯度备份求的那次梯度，Free AT则是因为N除以K了。

• 由于FreeLB利用了多步K积累的梯度再做更新，对梯度的估计更加精准，而且不存在FreeAT那样连续利用多个相同的min-batch进行梯度更新的问题。
• 相比于YOPO-m-n，FreeLB也是将K步(这里指m)中的梯度综合后再更新参数，不同的是其没有更进一步的n层，即使有，也是n个完全相同的值。
• 为什么论文成这种算法为Large Batch呢？在梯度下降时，我们使用的梯度是基于[X+r1,X+r2,…,X+rk]进行计算的，这可以理解为近似的对K个不同batch的样本进行平均，所以相当于虚拟的增大了样本的数量。

4.7 SMART(SMoothness-inducing Adversarial Regularization),ACL 2020

4.7.1 核心思想

之前我们看到的所有操作基本都是基于 Min-Max 的目标函数 ，但是在SMART却放弃了Min-Max公式，选择通过正则项Smoothness-inducing Adversarial Regularization完成对抗学习。为了解决这个新的目标函数作者又提出了优化算法Bregman Proximal Point Optimization，这就是 SMART 的两个主要内容。

SMART论文中提出了两个方法：

1.对抗正则 SMoothness-inducing Adversarial Regularization，提升模型鲁棒性。

2.优化算法 Bregman proximal point optimization，避免灾难性遗忘。

第一种参考了半监督对抗训练，对抗的目标是最大化扰动前后的输出，在分类任务时loss采用对称的KL散度，回归任务时使用平方损失。

SMART的算法和PGD相似，也是迭代K步找到最优r，然后更新梯度。

4.8 VAT虚拟对抗训练,ACL 2020

4.8.1 研究动机

为了解决当前的预训练模型（文中用BERT和ROBERTa）泛化性和鲁棒性不足的问题，并且当前对抗训练虽然可以增强鲁棒性，但会损害泛化性的问题，提出了通用的语言模型对抗式训练算法：ALUM。

该模型是一种半监督学习的模型，相比于其他对抗式学习不同之处，例如FGSM、FGM、PGD等，ALUM是加入了无标签数据去优化模型参数。所以在训练过程中，计算样本、对抗样本的logits的DL散度得到对应的损失。

4.8.2 算法

1. 循环epoch
2. 循环数据集，每次产生一个batch_size大小的数据
3. 生成一个扰动δ , δ 服从均作为0，方差为1高斯分布
4. 循环K次，理论K越大效果越好，实际使用K=1，减少计算量
5. 计算实际输入的输出和对抗样本的实际输入的DL散度Loss，并计算梯度
6. 扰动正则化
7. 循环K次结束
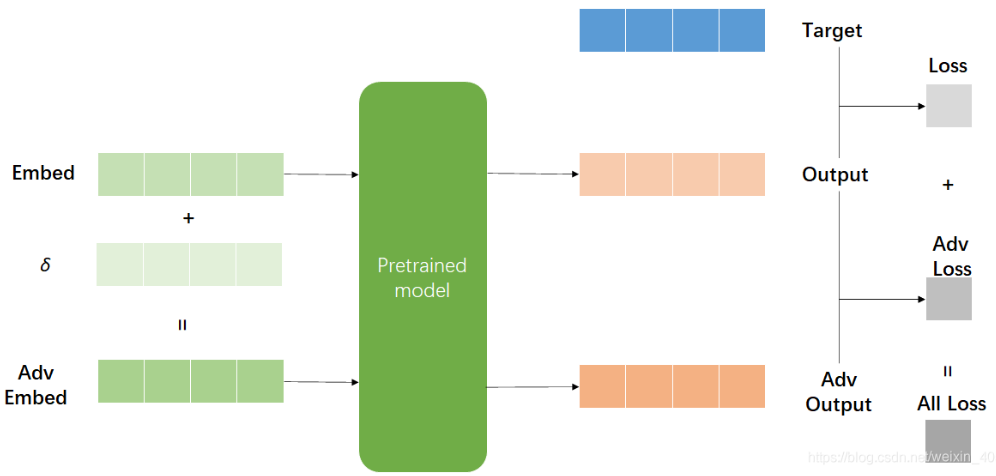
8. 计算模型的Loss（带标签数据loss+虚拟对抗Loss）计算梯度更新参数，α是增强对抗学习的比例，预训练设置为10，下游任务设置为1。

最后我们需要的是最小化Loss，最大化Adv Loss，最后我们的目标是：