- 1牛客网华为OD前端岗位,面试题库练习记录01_华为od前端面试题
- 2华为ensp 二层交换机的基础配置_华为二层交换机配置
- 3springboot集成rabbitmq商品秒杀业务实战(流量削峰)_rabbitmq削峰限流怎么做
- 4为什么我电脑的所有浏览器都开不了网页_所有浏览器都无法打开网页
- 5C#调用python的四种方法
- 6ES 8,大数据开发2024面试题
- 7身份证实名接口和身份证OCR接口的组合使用
- 8Redis: 缓存过期、缓存雪崩、缓存穿透、缓存击穿(热点)、缓存并发(热点)、多级缓存、布隆过滤器_缓存有失效时间吗
- 9R语言实现GWAS结果显著SNP位点归类提取与变异类型转化_从gwas中提取目标基因的相关参数
- 10【前端】npm常用命令
NLP笔记之word2vec算法(1)--Skip-gram算法原理+数学推导
赞
踩
目录
1.One-hot Vector
在自然语言处理(NLP)中,为了让计算机可以识别我们的自然语言,比如中文,英语等等,需要将自然语言进行向量化,即用一个向量来表示一个单词,一个句子或者一篇文章,最基本的向量表示方式叫做one-hot vector,也叫作独热向量,该类向量是指只有一个位置为1,其他位置全为0的向量。举个例子,有个句子是 { 我们,爱,打,手机,游戏 },对其中的每个字进行向量化,可以得到
我们 : [1, 0, 0, 0 ,0]
爱: [0, 1, 0, 0, 0]
打: [0, 0, 1, 0, 0]
手机: [0, 0, 0, 1, 0]
游戏: [0, 0, 0, 0, 1]
每个词语都对应于一个单独的one-hot向量,不同的词语对应于不同的one-hot向量,但是每个词语和one-hot向量之间的对应关系是随意的,也就是说爱的one-hot向量为 [1, 0, 0, 0 ,0],我们的one-hot向量为[0, 1, 0, 0, 0]也是完全没问题的,总的来说,就是指不同的词语要用不同的one-hot向量进行表示,但是对应关系是随意的,那么要用多少维度,多少个的one-hot向量来表示一个句子呢?
答案是一个句子进行分词后总共分为了几个部分,如上面例子中的5部分,就用多少维度的向量来进行表示每个词语,如上例中的向量是5维的,然后分成了几个词语,就总共有几个one-hot向量,当然也可以用大于5维的维度来表示每个one-hot向量,但是这样就会造成明显的浪费。
也就是说如果有一个词典Dict,它里面词语的数量为V,那么用one-hot进行表示的话,就总共有V个向量,每个向量的维度为V(这里维度也可以大于V,但是会造成维度上的浪费),并且每个向量都不一样。这样就将每个词语用向量进行了表示,但one-hot 向量在实际使用中存在很多不足的地方,因此在实际NLP任务中,直接用one-hot 向量表示词语来进行训练的情况非常罕见,要么不使用one-hot,要么进行一些修改。
One-hot vector的缺点在于:
1. 无法使用该方法进行单词之间的相似度计算,比如余弦相似度
![]()
任意两个one-hot向量之间的余弦相似度结果都为0,因为任意两个向量之间都是正交垂直的,所有结果没有区分度,无法区分词语之间的相似程度。
2. 如果词典的词语个数V 非常庞大的情况下,就会存在V个ont-hot向量,并且每个向量的维度也是V, 所占据的资源和内存空间非常庞大,而且维度为V的向量中,只有一个位置为1,剩余的V-1个位置都为0,从矩阵学的角度来说,也就是说这样的向量,这样的向量所组成的矩阵非常稀疏,非常sparsity,显然这样稀疏的表示方法不适用于我们的要求。
3. 因为每个词语都对应于一个one-hot向量,但是对应关系是随意的,想对应哪个one-hot向量都可以,只要没有重复就可以,这样的表示方式就无法表明词语之间的关系和联系,因为你想用哪个one-hot向量表示都行,所以每个向量之间没有任意的联系,是彼此独立的,但是在实际情况中,一个句子中的词语可能存在上下文的联系和其他的关系,因此这样表示不太符合实际情形。
所以在2013年Google提出了Word2vec,来解决one-hot的缺陷,并且提出了一系列新的表示自然语言的向量表示方法,在这里提出一个专业名次,在NLP领域中,把词语用向量来进行的技术统一叫做词嵌入(word embedding)或者 word representation。把句子用向量来进行表示,则就叫做sentence embedding。
Word2vec这种 word embedding表示方式的优点在于它可以表示词语之间的联系,如果将大于二维的word embedding向量投射到二维空间中,可以看出它使得关系比较紧密的词语之间距离更近,相对应的,比较疏远的词语就会距离相对更大,比如乒乓球可能和乒乓球拍的距离就会比较近,乒乓球和笔记本之类词语的距离就会比较远。这样的一个表示形式就可以更好的让我们了解到词语之间的关系,也可以更好的对于一个句子进行操作。

并且每个词语的表示维度也不受限于词典的词语数量了,理论上,可以自定义维度来表示每个词语了,但是每个词语的维度都是一样的,只是维度不一定等于词典的大小V了,在实际情况中,维度的取值可能会有一些经验之谈,就是某些特定的维度在实际中表现更好,但是不考虑性能的话,维度就可以进行自定义了。因此对于这样的可以表示词语之间的关系的word embedding,可以自定义维度的word embedding,我们给它一个专有名词,叫做分布式表征(Distributed Representation),不过在实际情况中,直接叫做word embedding是更为常见的。因为在实际情况中,word embedding基本指的就是Distributed Representation。
2.Word2vec
下面我们详细介绍word2vec模型的细节。
word2vec中提出了两种模型来进行word embedding,分别是Skip-gram 和 CBOW(continuous bag of words),这两种模型的概念在Word2vec之前就已经提出来了。
下面先对两种模型做个简要的介绍:
Skip-gram : 给定中心词,预测窗口内的上下文的词
CBOW : 给定窗口内的上下文的词, 预测中心词
可以看出两种模型属于相反的一个关系,下面分别对两种模型进行相应的介绍。
2.1 Skip-gram模型
Skip-gram是通过中心词来推断上下文一定窗口内的单词,中心词center word就是指所给定的词,也就是模型所输入的词;上下文一定窗口内的单词叫做context words,窗口是指window size,也就是指定一个window size的值,所要预测的词语就是和中心词距离在window size内的所有其他词。 这里用个例子来说。

如果center word此时为learning的话,并且window size设为4,那么context words就是前面的四个单词an, efficient, method, for 和后面的四个单词 high, quality, distributed, vector,window size是可以自己设定的,设置为1,2, 3 ....都是可以的。如果center word的位置在于句子起始或者句子末尾时,例如center word 为 efficient 时,window size为4的情况下,context words就只有 an 和 method, for,learning , high了,就是说如果中心词前面或者后面的词语数量小于 window size的话,context words就只包含所存在的单词而已。
所以skip-gram 所做的事情就是给定一个中心词,去预测一些在给定窗口内的它的上下文的词,也就是输入一个词,去预测多个词的一种模型。
2.2 CBOW 模型
CBOW模型是和Skip-gram模型反过来的一种方式,根据上面的图,如果给定window size为3, 输入的context words 为 efficient , method, for 和 high ,quality, distributed,那么我们所要预测的结果就是其所对应的中心词,也就是learning。
所以CBOW 所做的事情就是给定一些窗口内的上下文的词, 去预测中心词,也就是输入多个词,去预测一个词的一种模型。
因为Skip-gram 模型 和 CBOW 模型两者实现细节都差不多,只是方向相反而已,所以这里仅对Skip-gram模型进行原理和数学上的推导,相信掌握了Skip-gram模型推导后,再进行CBOW模型的推导就会十分简单了。
3.Skip-gram原理+数学推导
因此从上面我们知道了Skip-gram模型是根据中心词,预测context words的模型,我们这里给出skip-gram的一个前一部分的流程图,接下来会详细讲解图片的意思。
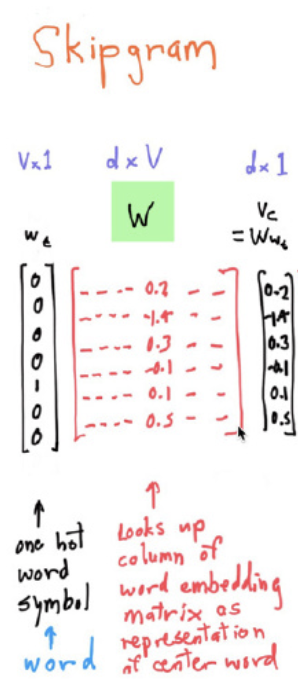
前面我们说到one-hot向量在实际情景中不会直接送入模型作为参数进行训练,因此在skip-gram中对于输入的中心词,我们会先将它用one-hot 向量进行表示,就如图中最左边的列向量所示,图中所画的是列向量,但是我们实际推导中还是将其看作行向量。如果此时的词典大小为V, 那么one-hot向量的维度我们设定为 V ,所以每个向量维度为(1, V) , 我们知道实际使用中用的word embedding都是 Distributed Representation , 并且维度可以自己进行定义,因此在这里我们将word embedding的维度设为 d ,那么word embedding的维度就为 (1,d),那么我们要将(1,V)的one-hot向量转换成
(1,d)的word embedding 的话,就需要一个维度为(V,d)的一个矩阵W,这个矩阵W我们叫做系数矩阵, 这个矩阵W就是我们所要更新的参数,我们所求的也就是这个矩阵W ,现在看这个矩阵W可能十分陌生,但是我们现在只需要记住这个矩阵W就是我们所求的参数就可以了,接下来会进行详细的讲解。

上图中的 Input layer 指代的就是我们的one-hot向量, W 就是系数矩阵, Hideden layer就是 计算所得的word embedding,我们知道word embedding的维度是(1, d)。 又因为skip-gram模型是根据输入的中心词,预测上下文内的多个单词的,比如window size为c的话, 我们最后所要做的事情就是从词典大小为V 的词典中选出 2c 个词语作为结果 ,但此时我们的word embedding的维度为(1, d), 而不是我们所想要的(1, V), 所以我们需要个W' 矩阵来将word embedding 再转换为(1, V)的向量 ,此时W’ 矩阵的维度为(d, V)。 在得到(1, V)的向量后,经过一个softmax 函数,将V个值转换成了V个概率值,然后从V个概率值中选出前2c个概率最大的位置,即为我们所要求的结果 。这里所讲的已经是模型的预测过程了,因为前面我们跳过了前面 W 矩阵的细节,接下来我们介绍模型的训练过程,也就是计算参数矩阵 W 的过程。
我们在这里先讲解一个概念,Lookup Table , 因为我们前面讲到one-hot 向量 经过一个系数矩阵W会得到 word embedding ,但是如果one-hot向量的维度非常的大的情况下,也就是词典的大小 V 非常大的情况下,计算word embedding也不是一件很容易的事情,对于此,我们可以根据one-hot向量的特性,使得计算变得比较简单。如下图所示:

比如系数矩阵W 如图中所示,是个(5, 3)的矩阵,因为one-hot向量只有一个位置为1,其余位置为0, 所以在这里的计算我们可以不用进行太多复杂的操作,可以很明显的看出,在one-hot向量中为1的位置是第4个位置,其对应的word embedding 就是系数矩阵W 的第4行。 没错了,计算出来的word embedding向量,和我们单词在one-hot的位置是有关系的 ,在one-hot中1的位置是几,word embedding对应的就是系数矩阵W中的第几行,所以我们称这样的关系叫做单映射关系,简单理解就是:如果集合A→集合B存在映射关系,并且集合A中任意不同的元素,在集合B中有不同的映射,这样做的目的是,保证每个单词都是独立的,都是不同的,过程就是,将one-hot编码后的词向量,通过一个系数矩阵W,映射到一个更低纬度的空间。这样的映射使得我们不需要进行太多的计算,因此也称系数矩阵W 为Lookup Table。
接下来就是最为复杂的数学推导部分了,对于高数部分有所欠缺的同学,需要补足下高数部分的知识可能才可以更好地理解。
举个例子
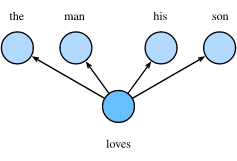
假设文本序列是“the”“man”“loves”“his”“son”。
以“loves”作为中心词,设背景窗口大小为2。如图所示,skip-gram所关心的是,给定中心词“loves”,生成与它距离不超过2个词的背景词“the”“man”“his”“son”的条件概率,
P(“the",“man",“his",“son"∣“loves").
假设给定中心词的情况下,背景词的生成是相互独立的,那么上式可以改写成
P(“the"∣“loves")⋅P(“man"∣“loves")⋅P(“his"∣“loves")⋅P(“son"∣“loves").
那么这些概率要怎么求呢?
在skip-gram模型中, 每个词都存在两个d维的向量,一个是中心词时的向量v,一个是为context时的向量u,这两个维度为d的向量用来计算条件概率 ,这里的d维指的就是系数矩阵W的列向的那个维度,因为系数矩阵的维度是(V,d)。
假设这个词在词典中索引为 i ,当它为中心词时向量表示为![]() ∈
∈ ![]() ,而为context (背景词)时向量表示为
,而为context (背景词)时向量表示为![]() ∈
∈ ![]() 。设中心词
。设中心词![]() 在词典中索引为c,背景词
在词典中索引为c,背景词![]() 在词典中索引为o,给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到:
在词典中索引为o,给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到:

上面的公式还是比较容易理解的,由中心词来推断背景词,注意整个过程的输入是(中心词向量,背景词向量),根据上面的所提到的背景词之间都是独立的,这种时候,可以把概率写成连乘的形式:

上述公式中,T表示窗口中心词的位置,m表示的窗口的大小。这样就可以计算出每个中心词推断背景词的概率,而我们在输入的时候给出了背景词的向量,此时只需要最大化背景词的输出概率即可。 基于这样的想法,我们会想到极大化似然估计的方式。但是一个函数的最大值往往不容易计算,因此,我们可以通过对函数进行变换,从而改变函数的增减性,以便优化。
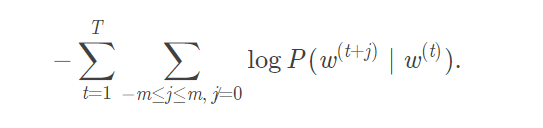
上面的变换,非常容易理解:1)对数似然变换,因为对数是单调递增,不会影响原函数的单调性;2)添加负号“-”,会使得原函数的单调性对调。
最小化损失函数,我们最容易想到的就是梯度下降法。在使用梯度下降法之前,我们要把我们的损失函数定义出来,毕竟上面的式子是一个概率,下面吧softmax的计算结果带入得到:

损失函数已经得到了,我们的目标就是最小化它,优化它之前我们要搞清楚我们的参数是谁?没错,我们的参数是中心词和背景词,那对于这样的一个函数显然是非凸函数,因此,我们要做一个假设,假设在对中心词权重更新时,背景词的权重是固定的,然后在以同样的方式来更新背景词的权重。
既然是梯度下降法,那么就求导计算梯度吧:

这里就计算出来了中心词的梯度,可以根据这个梯度进行迭代更新。对于背景词的更新是同样的方法,即固定中心词,然后对背景词进行更新。
训练结束后,对于词典中的任一索引为 i 的词,我们均得到该词作为中心词和背景词的两组词向量![]() 和
和![]()
在词典中所有的词都有机会被当做是“中心词”和“背景词”,那么在更新的时候,都会被更新一遍,这种时候该怎么确定一个词的向量到底该怎么选择呢?
在自然语言处理应用中,我们一般使用skip-gram模型的中心词向量作为词的表征向量。
上面高数部分的推导是引用了小小的天和蜗牛非常好的高数推导图片,在此表明。
通过上面的推导,我想我们可以知道这里所提的u,v 向量就是上面我们所指的系数矩阵W。因为当固定context时,中心词u的向量就是系数矩阵W中中心词所对应的那一行,context words 的向量也就是系数矩阵W中每个context word 所对应的那一行。因为我们所做的就是固定context,更新所有的中心词,然后固定中心词,更新所有的context,每次所更新的向量就是系数矩阵W中的一行,所以将句子中每个词都作为中心词来进行更新后,系数矩阵W也就得到了全部的更新。
这里存在一个问题,从刚刚最终的梯度公式中,存在着一个参数![]() ,我们知道这个参数代表的含义是词典中单词的个数,通常这个个数会非常大,这时候我们在进行迭代的时候对系统消耗也是巨大的,因为每走一步就要对所有的单词进行一次矩阵运算。这种时候该如何进行优化呢?
,我们知道这个参数代表的含义是词典中单词的个数,通常这个个数会非常大,这时候我们在进行迭代的时候对系统消耗也是巨大的,因为每走一步就要对所有的单词进行一次矩阵运算。这种时候该如何进行优化呢?
在Word2vec中采用了两种方式进行优化:
Hierarchical softmax
Negative Sampling
对于这两种优化方式,在后续的文章中有时间我会继续介绍它们的详情。
欢迎转载,转载请附上原文出处链接。


