骨骼动画——论文与代码精读《Phase-Functioned Neural Networks for Character Control》

前言

最近一直玩CV，对之前学的动捕知识都忘得差不多了，最近要好好总结一下一直以来学习的内容，不能学了忘。对2017年的SIGGRAPH论文《Phase-Functioned Neural Networks for Character Control》进行一波深入剖析吧，结合源码。
额外多句嘴，这一系列的研究有：

• 在2016年SIGGRAPH有一篇《A Deep Learning Framework For Character Motion Synthis and Editing》也是做到了控制骨骼动画沿着轨迹走跑、大小步、面向任意方向的运动等。
• 在2018年SIGGRAPH上进一步做到了四肢行走动物的行为上《Mode-Adaptive Neural Networks for Quadruped Motion Control》，也是地形自适应以及各种控制参数走跑跳站立之类的
• 在2019年SIGGRAPH Asia上又提出了《Neural State Machine for Character-Scene Interactions》，处理更复杂的游戏场景的交互，比如搬箱子、坐凳子之类的。

开源地址：
Daniel Holden大佬的主页
unity项目AI4Animation地址(17-19年论文的实现)

论文简介

通常情况下，神经网络训练完毕以后，在使用阶段，权重是不会动态改变的。但是在做动捕的时候，通常会用某个控制参数去改变权重，将下一帧的运动风格导向到指定行为状态。比如本来是走运动，如果输入一直是走，权重又不变，那么后面所有生成的动画帧都很难过渡到跑或者其它运动风格。通过某个控制参数去动态指向性地调整权重，就能将运动从走的特征空间拉到跑的隐特征空间，再从特征空间重构骨骼动画数据(欧拉角、3D坐标等)。

PFNN就是使用Phase Function相位函数去循环动态改变权重，这个Phase在文中是用于指定脚的落地状态。在$4.1$章节的Phase Labelling中有这样一句话：

the right foot comes in contact with the ground and assigning a phase of 0, observing the frames when the left foot comes in contact with the ground and assigning a phase of π, and observing when the next right foot contact happens and assigning a phase of 2π
1

意思是右脚着地时相位为$0$，左脚着地时相位为$\pi$，下次右脚着地时相位为$2\pi$

整篇论文包含三个部分：预处理、训练、运行时。接下来按照顺序把文章和代码对应起来。

截了一张图，说明一下它的功能。

从上图地面上那一条线，可以看出，它可以根据你的手柄控制计算出未来的一段轨迹，人的运动方向与轨迹的方向不一定相同，可以走也可以跑，还能爬坡。

预处理

论文的第4章节Data Accquisition & Processing与对应代码generate_database.py和generate_patches.py的对应解读。

数据总量

动捕各种地形(障碍物，斜坡，平台等)，各种行为(走、慢跑、跑、蹲伏、跳跃、不同步长等)，大约一个小时的数据，60FPS，1.5G。还是CMU的BVH动捕数据格式，包括30个关节的旋转角，1个根关节的位置。

数据标签

相位标签:

半自动标记相位值。脚着地的时候，可以计算脚跟和脚尖的速度，设置一个阈值判别是否落地，再人工矫正一下自动标记的标签。当脚着地时间得到了以后，把右脚刚着地时的相位phase标记为$0$，把左脚刚着地时的相位标记为$\pi$，把下次右脚着地的相位标记为$2\pi$。他们之间的中间帧的相位值就用线性插值就可以了。

这个在开源代码的data/animation/***.phase中预先把所有的数据集标记好了，我们不需要再去为每个数据集制作相位标签。随便找个数据验证一下。

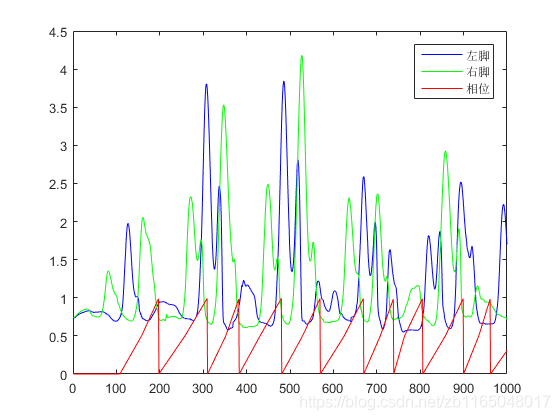
可以发现，相位值的确是插值出来的，但是范围被归一化到$(0,1)$之间了，红色和绿色分别代表左右脚的高度状况，当右脚落地时候，绿线高度最低，可以看出来刺客红线(相位值)为0或者1。

步态标签：

二值标签向量，表示不同场景中的不同运动。这个需要人工标记。从data/***.gait和data/***_gait.txt中可以看出来，代表8种运动风格(stand,walk,jog,run,crouch,jump,crawl,scol/ecol)，其中***.gait的每一行代表当前帧的运动属于这八种风格的某几种。验证三帧：

步态为：

1.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.30667 0.00000 0.00000 0.69333 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 1.00000 0.00000 0.00000 0.00000 0.00000
1
2
3

帧动画为：

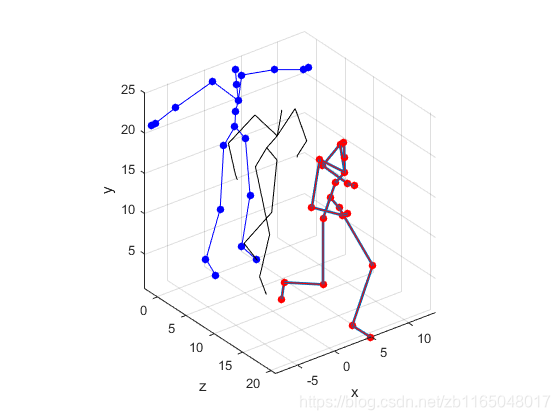
三帧可视化结果, 不难看出, 第一个维度代表站立(第一帧), 第四个维度代表跑(第三帧), 中间一帧代表(风格倾向跑, 但是刚从站立变化过来)。而且这个标签与作者说的binary vector不符。

其它：

此外还提供了一下几类数据：

**_footsteps.txt：并无实际意义, 随机选取的帧段, 便于后续的地形矫正处理

hmp_**_smooth.txt:地形文件。

验证一下_footsteps，可视化前五十个帧段看看，文件的前五十个帧段的索引为

108 198 310 383 481 570 670 739 806 900 962 1072 1124 1206 1291 1401 1487 1583 1677 1734 1806 1888 1946 2040 2137 2223 2304 2397 2491 2549 2631 2725 2783 2865 2960 3035 3142 3223 3277 3383 3458 3518 3615 3698 3777 3863 3975 4071 4156 4258
1

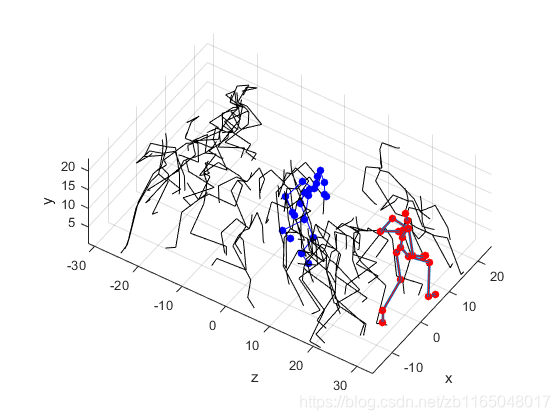
可视化地形看看，左边是Matlab可视化，右边是论文demo的地形

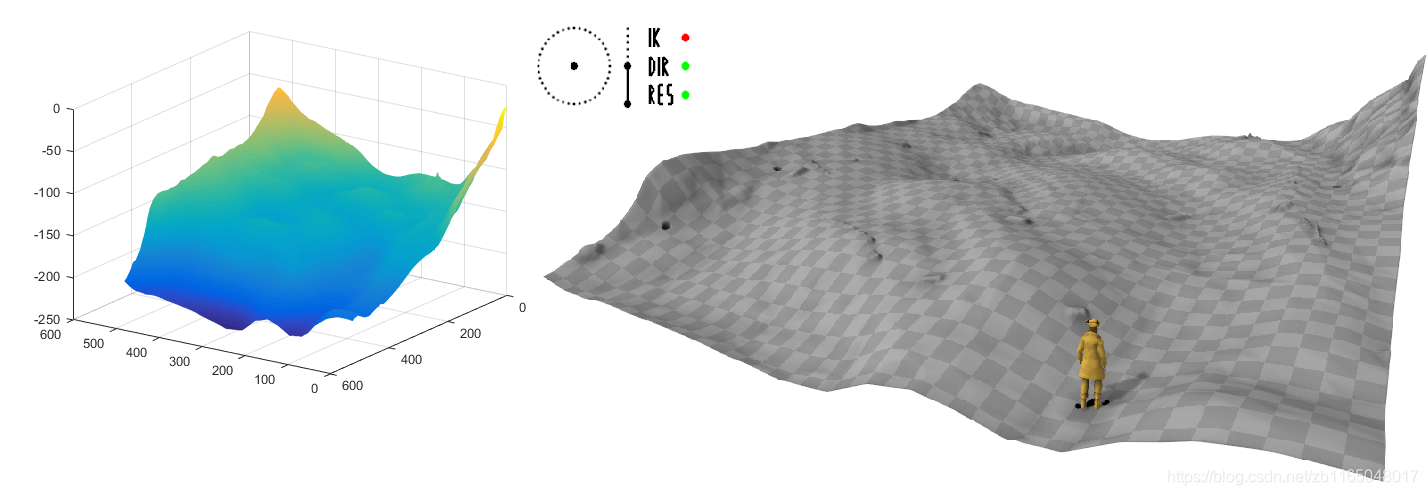
数据集预处理——4.1章节

一、读取BVH文件

将运动数据转化为某种结构存储, 此结构包含:

• rotations: 原始欧拉角数据转换的四元数(关于四元数的解读)
• positions: 根关节位置, 各关节的偏移(除了根关节, 其它各关节都一样, 从BVH文件的骨骼记录HIERARCHY获取),对于每一帧的维度为$31\times 3$
• offset: 除了根关节以外的各关节的偏移, 与positions其它关节偏移一样的数据

随后将offset和positions乘以缩放比例$5.644$, 下采样数据(两帧间隔), 以下所有过程都先被下采样.

【注】具体地python与mocap相关四元数操作方法戳这里

二、结合相位phase和步态gait文件对运动数据进行处理

此步骤主要是针对文章深度学习模型的输出和输出做一个时序帧块的处理, 分别需要分别提取：

• 输入数据($120$帧)的根关节位置, 根关节朝向, 步态,当前帧局部位置,当前帧局部速度;
• 输出数据(60帧)的根关节x,z方向速度**, 根关节绕垂直方向的旋转速度，每连续60帧的中间帧触地情况，根关节的x,z坐标, 根关节x,z方向的旋转,**中间帧的局部位置, 局部速度,局部旋转

具体计算方法如下(generate_database.py的$449$行开始)：

①读取步态文件.gait，第$483$行将慢跑(索引$2$)和跑(索引$3$)合起来当做一种运动风格、crouch(索引$4$)和crawl(索引$6$)当做同一种运动风格,这样整体的运动风格就从$8$种缩减到$4$种, 即步态gait的维度是$6$

gait = np.loadtxt(data.replace('.bvh', '.gait'))[::2]
gait = np.concatenate([
        gait[:,0:1],
        gait[:,1:2],
        gait[:,2:3] + gait[:,3:4],
        gait[:,4:5] + gait[:,6:7],
        gait[:,5:6],
        gait[:,7:8]
    ], axis=-1)
1
2
3
4
5
6
7
8
9

②读取相位值文件.phase, 范围$(0\to 1)$

③第$494$行开始进入处理函数

Pc, Xc, Yc = process_data(anim, phase, gait, type=type)
1

依据前向运动学分别提取:

• 每帧每个关节的全局旋转矩阵$Trans{M}_{global}$:

  global_xforms = Animation.transforms_global(anim)
  1

  先将动画所表示的四元数数据转换为各关节的局部旋转矩阵$T{M}_{local}$, 并使用各关节的位置(根关节)或者偏移(其它30个关节)对局部旋转矩阵填充,这项数据存储于positions中, 对于每一帧都得到$31\times 4\times 4$的局部矩阵
  T r a n s M l o c a l i = [ T M p o s i t i o n i 0 1 ] TransM_{local}^i=

  $$\begin{bmatrix} TM&position_i\\ 0&1 \end{bmatrix}$$ TransMlocali​=[TM0​positioni​1​]
  对于除了根关节以外的30个关节全局旋转矩阵计算方法如下
  $$Trans{M}_{global}^i=Trans{M}_{global}^{i\_parent}\ast Trans{M}_{local}^i$$
  上式的起点是根关节,对于根关节$Trans{M}_{global}^{root}=Trans{M}_{local}^{root}$

• 每帧每个关节的全局位置$global\_position$

  global_positions = global_xforms[:,:,:3,3] / global_xforms[:,:,3:,3]
  1

  其实就是$Trans{M}_{gloabal}$的最后一列的前三行, 即为每个关节的全局坐标

• 每帧每关节的全局旋转四元数

  global_rotations = Quaternions.from_transforms(global_xforms)
  1

  将$Trans{M}_{global}$的旋转矩阵逆推为四元数表示

④提取每帧根关节的旋转角度$root\_rotation$

""" Extract Forward Direction """
    
    sdr_l, sdr_r, hip_l, hip_r = 18, 25, 2, 7
    across = (
        (global_positions[:,sdr_l] - global_positions[:,sdr_r]) + 
        (global_positions[:,hip_l] - global_positions[:,hip_r]))
    across = across / np.sqrt((across**2).sum(axis=-1))[...,np.newaxis]
    
    """ Smooth Forward Direction """
    
    direction_filterwidth = 20
    forward = filters.gaussian_filter1d(
        np.cross(across, np.array([[0,1,0]])), direction_filterwidth, axis=0, mode='nearest')    
    forward = forward / np.sqrt((forward**2).sum(axis=-1))[...,np.newaxis]

    root_rotation = Quaternions.between(forward, 
        np.array([[0,0,1]]).repeat(len(forward), axis=0))[:,np.newaxis] 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

原理是利用双肩向量$\overrightarrow{Shoulder}$和髋部$\overrightarrow{hips}$向量加和与y轴向量做叉乘,得到前进方向$\overrightarrow{forward}$, 最后计算其与z轴正向夹角的四元数表示即为整个人体面向方向
$$\begin{gathered} \overrightarrow{forward}=(\overrightarrow{Shoulder}+\overrightarrow{hips})\times \overrightarrow{y_{axis}} \\ root\_rotation=<\overrightarrow{forward},\overrightarrow{z_{axis}}{>}_{夹角的四元数表示} \end{gathered}$$

⑤计算局部空间信息

""" Local Space """
    local_positions = global_positions.copy()
    # 各帧中所有关节与跟关节的x,z坐标差值，获取3D向量
    local_positions[:,:,0] = local_positions[:,:,0] - local_positions[:,0:1,0]
    local_positions[:,:,2] = local_positions[:,:,2] - local_positions[:,0:1,2]
    # 沿着方向的各种变量，消除绝对方向的影响，以当前人体朝向为基准，计算身体其它各元素 
    local_positions = root_rotation[:-1] * local_positions[:-1]#所有关节3D向量*人体朝向
    local_velocities = root_rotation[:-1] *  (global_positions[1:] - global_positions[:-1])#沿着人体方向的各关节速度
    local_rotations = abs((root_rotation[:-1] * global_rotations[:-1])).log()#沿着人体方向的各关节方向
    
    root_velocity = root_rotation[:-1] * (global_positions[1:,0:1] - global_positions[:-1,0:1]) #根关节的移动速度
    root_rvelocity = Pivots.from_quaternions(root_rotation[1:] * -root_rotation[:-1]).ps#跟关节的旋转速度
1
2
3
4
5
6
7
8
9
10
11
12

原理是以第一帧为参考帧, 计算其余每帧的31个关节的局部位置, 速度, 旋转量, 根关节的移动速度, 绕y轴的旋转速度

• 第$i$帧向局部位置变化$local\_positio{n}^i$,维度$31\times 3$:
  $$\begin{gathered} local\_positio{n}_{xz}^i=global\_positio{n}_{xz}^i-global\_positio{n}_{xz}^1 \\ local\_positio{n}_y^i=global\_positio{n}_y^i \\ local\_positio{n}_{xyz}^i=root\_rotatio{n}^i\ast local\_positio{n}_{xyz}^i \end{gathered}$$

• 第$i$帧的局部速度变化$local\_ve{l}^i$,维度$31\times 3$:
  $$local\_vel=root\_rotatio{n}^i\ast (global\_positio{n}^i-global\_positio{n}^{i-1})$$

• 第$i$帧的局部旋转变化$local\_rotation$,维度$31\times 3$:
  $$local\_rotatio{n}_i=|(root\_rotatio{n}^i\ast Trans{M}_{global}^i){|}_{正切值计算}$$

• 第$i$帧根关节移动速度$root\_ve{l}^i$, 其实就等于$local\_vel$中记录的根关节速度
  $$root\_ve{l}^i=root\_rotatio{n}^i\ast (global\_positio{n}_z^i-global\_positio{n}_z^{i-1})$$

• 第$i$帧绕y轴旋转速度$root\_rve{l}^i$, 记录根关节的旋转速度
  $$root\_rve{l}^i=root\_rotatio{n}^i\ast (-rotatio{n}^{i-1}{)}_{正切值计算}$$

⑥计算脚触地状态
针对每只脚的脚跟和脚尖, 利用相邻帧的差值是否小于某个阈值来判断, 分别判断左脚的脚跟和脚尖的触地状态$feet\_l$和右脚的脚跟和脚尖的触地状态$feet\_r$,触地为$1$,否则为$0$, 分别存储脚跟和脚尖的触地信息

 """ Foot Contacts """
    
    fid_l, fid_r = np.array([4,5]), np.array([9,10])
    velfactor = np.array([0.02, 0.02])
    
    feet_l_x = (global_positions[1:,fid_l,0] - global_positions[:-1,fid_l,0])**2
    feet_l_y = (global_positions[1:,fid_l,1] - global_positions[:-1,fid_l,1])**2
    feet_l_z = (global_positions[1:,fid_l,2] - global_positions[:-1,fid_l,2])**2
    feet_l = (((feet_l_x + feet_l_y + feet_l_z) < velfactor)).astype(np.float)
    
    feet_r_x = (global_positions[1:,fid_r,0] - global_positions[:-1,fid_r,0])**2
    feet_r_y = (global_positions[1:,fid_r,1] - global_positions[:-1,fid_r,1])**2
    feet_r_z = (global_positions[1:,fid_r,2] - global_positions[:-1,fid_r,2])**2
    feet_r = (((feet_r_x + feet_r_y + feet_r_z) < velfactor)).astype(np.float)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

⑦相位值变化量$dphase$

""" Phase """
    
dphase = phase[1:] - phase[:-1]
dphase[dphase < 0] = (1.0-phase[:-1]+phase[1:])[dphase < 0]
1
2
3
4

$$\begin{gathered} dphas{e}^i=dphas{e}^i-dphas{e}^{i-1} \\ dpha{e}^i=1+dpha{e}^{i}ifdphas{e}^i<0 \end{gathered}$$

⑧flat风格中步态数据矫正$gait$

""" Adjust Crouching Gait Value """
    
    if type == 'flat':
        crouch_low, crouch_high = 80, 130
        head = 16
        gait[:-1,3] = 1 - np.clip((global_positions[:-1,head,1] - 80) / (130 - 80), 0, 1)
        gait[-1,3] = gait[-2,3]
1
2
3
4
5
6
7

在弯腰走和平地走的时候, 头部的高度必须限制在$(80,130)$的范围, 所以对于从.gait文件中读取的crouch(在$8$维中索引是$4$,在合并后的$6$维中索引为$3$)步态值
g a i t 3 i = { 0 , g l o b a l _ p o s i t i o n h e a d < 80 1 − g l o b a l _ p o s i t i o n h e a d − 80 130 − 80 , 80 ≤ g l o b a l _ p o s i t i o n h e a d ≤ 130 1 , g l o b a l _ p o s i t i o n h e a d > 130 gait^i_3=

$$\begin{cases} 0,\quad global\_position_{head}<80\\ 1-\frac{global\_position_{head}-80}{130-80}, \quad 80\leq global\_position_{head}\leq 130\\ 1,\quad global\_position_{head}>130 \end{cases}$$ gait3i​=⎩⎪⎨⎪⎧​0,global_positionhead​<801−130−80global_positionhead​−80​,80≤global_positionhead​≤1301,global_positionhead​>130​
⑨组合成网络的输入输出中与人体有关的数据维度

	for i in range(window, len(anim)-window-1, 1):
        #选取windows=120的帧段，进行下采样
        rootposs = root_rotation[i:i+1,0] * (global_positions[i-window:i+window:10,0] - global_positions[i:i+1,0])#其余帧跟关节相对中间帧跟关节的位置变化(12,3)
        rootdirs = root_rotation[i:i+1,0] * forward[i-window:i+window:10]#12帧的前进方向
        rootgait = gait[i-window:i+window:10]#12帧的步态信息
        
        Pc.append(phase[i])
        
        Xc.append(np.hstack([
                rootposs[:,0].ravel(), rootposs[:,2].ravel(), # Trajectory Pos 12帧的跟关节位置变化量的x和z：1~12，13~24
                rootdirs[:,0].ravel(), rootdirs[:,2].ravel(), # Trajectory Dir 12帧的跟关节的方向变化x和z: 25~26，37~48
                rootgait[:,0].ravel(), rootgait[:,1].ravel(), # Trajectory Gait 12帧的步态信息:49~60,61~72
                rootgait[:,2].ravel(), rootgait[:,3].ravel(), #73~84,85~96
                rootgait[:,4].ravel(), rootgait[:,5].ravel(), #97~108,109~120
                local_positions[i-1].ravel(),  # Joint Pos 当前关节的局部位置121~213
                local_velocities[i-1].ravel(), # Joint Vel 当前关节的局部速度214~306
                ]))
        #把60帧段向后移一帧，代表未来的移动状态
        rootposs_next = root_rotation[i+1:i+2,0] * (global_positions[i+1:i+window+1:10,0] - global_positions[i+1:i+2,0])#下一个6帧中，其余帧相对于中间帧的位置
        rootdirs_next = root_rotation[i+1:i+2,0] * forward[i+1:i+window+1:10]  #下一个6帧方向
        
        Yc.append(np.hstack([
                root_velocity[i,0,0].ravel(), # Root Vel X 当前根关节的平移速度x 1
                root_velocity[i,0,2].ravel(), # Root Vel Y 当前根关节的平移速度z 2
                root_rvelocity[i].ravel(),    # Root Rot Vel 当前根关节的旋转速度 3
                dphase[i],                    # Change in Phase 相位变化量 4
                np.concatenate([feet_l[i], feet_r[i]], axis=-1), # Contacts着地状态 5~8
                rootposs_next[:,0].ravel(), rootposs_next[:,2].ravel(), # Next Trajectory Pos 未来6帧的根关节位置变化x和z 9~20
                rootdirs_next[:,0].ravel(), rootdirs_next[:,2].ravel(), # Next Trajectory Dir 未来6帧的跟关节方向变化x和z 21~32
                local_positions[i].ravel(),  # Joint Pos 当前帧局部位置信息 33~125
                local_velocities[i].ravel(), # Joint Vel 当前帧局部速度信息 126~218
                local_rotations[i].ravel()   # Joint Rot 当前帧旋转信息 219~311
                ]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

原理是对于输入,使用120帧(0~119)对应的帧窗口, 采样过后是60帧, 对采样后的运动数据的第60帧到末尾的第60帧之间的所有帧分别建立以其为中心的滑动窗口(包含此帧的左右各60帧,共120帧), 对于每个滑动窗口先计算:

• 帧窗口每帧相对于中间帧的位移量
  $root\_poss=root\_rotaio{n}^i\ast (global\_positio{n}_{root}^{(i-60:i+59)}-global\_positio{n}_{root}^i)$

• 帧窗口每帧的全局方向
  $$root\_dirs=root\_rotatio{n}^i\ast forwar{d}^{(i-60:i+59)}$$

• 帧窗口每帧的步态信息
  $$root\_gait=gai{t}^{(i-60:i+59)}$$

以上120帧的窗口被再次下采样10间隔, 变为12帧

模型输入关于人体部分维度(306维)详情:

• 帧窗口根关节的$xz$坐标与中间帧(第61帧)作为轨迹位置$root\_pos{s}_{xz}$,维度$12\times 2=24$
• 帧窗口根关节的$xz$方向作为人体朝向$root\_di{r}_{xz}$, 维度$12\times 2=24$
• 帧窗口每帧步态的作为步态输入$root\_gait$, 维度$12\times 6=72$
• 当前帧的所有关节的局部位置$local\_positions$, 维度$31\times 3=93$
• 当前帧的所有关节的局部速度$local\_vel$, 维度$31\times 3=93$

对于输出, 仅仅计算滑动窗口当前帧的后60帧(61~120)对应的运动信息:
$$\begin{gathered} root\_poss\_next=root\_rotatio{n}^{(i+1)}\ast (global\_positio{n}^{(i+1:i+60)}-global\_positio{n}^{(i+1)}) \\ root\_dir\_next=root\_rotatio{n}^{(i+1)}\ast forwar{d}^{(i+1:i+60)} \end{gathered}$$
模型输出关于人体部分维度(311维)详情:

• 帧窗口起始帧(即输入的中间帧)帧根关节$xz$方向速度$root\_vel$, 维度$1\times 2=2$
• 帧窗口起始帧的旋转速度, 维度$1\times 1=1$
• 起始帧的相位变化量$dphas{e}^i$,维度$1\times 1=1$
• 起始帧两只脚的脚跟和脚尖的触地状态$feet\_l^i,feet\_r^i$, 维度$1\times 2\times 2=4$
• 帧窗口每帧的根关节$xz$坐标作为预测轨迹,维度$6\times 2=12$
• 帧窗口每帧的根关节$xz$朝向作为预测人体朝向, 维度$6\times 2=12$
• 起始帧所有关节的位置$local\_positio{n}^i$,维度$31\times 3=93$
• 起始帧所有关节的速度$local\_ve{l}^i$, 维度$31\times 3=93$
• 起始帧所有关节的旋转量$local\_rotatio{n}^i$, 维度$31\ast 3=93$

数据集预处理——4.2章节

地形校正( chapter 4.2)

一、地形块采样(整个generate_patches.py)

针对heightmaps地形高度文件做小块截取, 处理方式是直接使用随机采样的方法, 包含对位置、朝向的随机采样, 大约包含20000个批块, 每块是$3\times 3$米的区域, 这些块用于后续的地形适应处理. 下图展示了随机采样的五个位置和朝向的大小为3*3米的地形区域

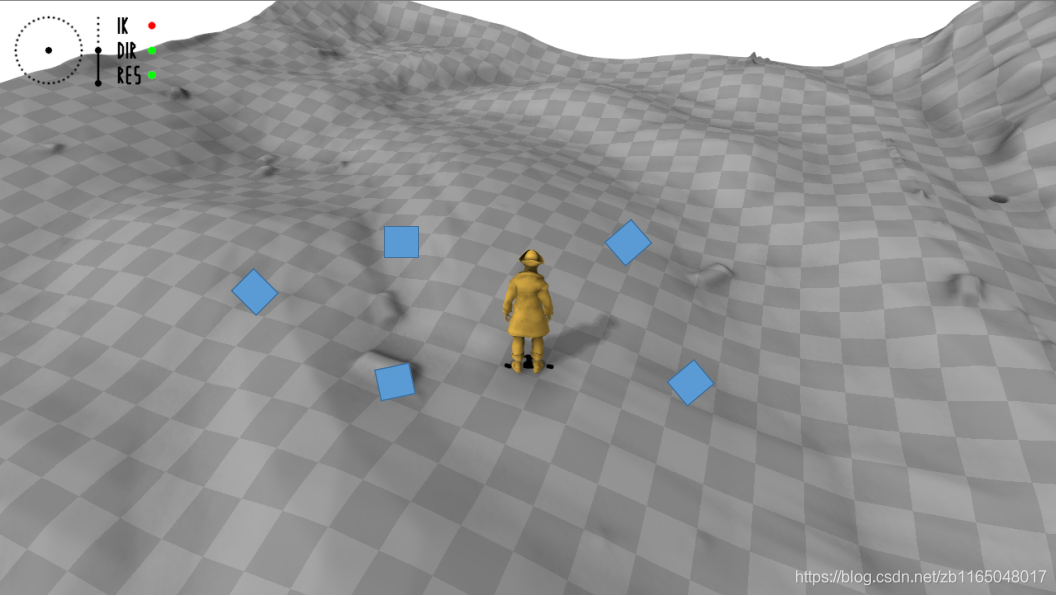
对应到具体的地形文件中,$3\times 3$米的区域对应$128\times 128$的数据块, 代表地形源文件中随机位置, 随机方向上的一块地形.

二、地形块相对帧段每帧脚高度的残差量

进入到generate_database.py的第$499$行，开始处理地形

""" For each Locomotion Cycle fit Terrains """
1

从footsteps.txt中读取相邻行的第一列数据作为处理帧段, 但是数据的索引是从第一行标记的起始帧的前60帧和第二行标记的结束帧的后60帧开始截取的帧段,进入每个帧段对应的十个地形调整过程. 具体如下:

①利用前向运动学提取当前帧段所有帧的全局坐标$global\_position$, 前进方向$root\_rotation$, 触地信息$feet\_l,feet\_r$

算法实现是process_heights中的代码：

 """ Do FK """
    
    global_xforms = Animation.transforms_global(anim)
    global_positions = global_xforms[:,:,:3,3] / global_xforms[:,:,3:,3]
    global_rotations = Quaternions.from_transforms(global_xforms)
    
    """ Extract Forward Direction """
    
    sdr_l, sdr_r, hip_l, hip_r = 18, 25, 2, 7
    across = (
        (global_positions[:,sdr_l] - global_positions[:,sdr_r]) + 
        (global_positions[:,hip_l] - global_positions[:,hip_r]))
    across = across / np.sqrt((across**2).sum(axis=-1))[...,np.newaxis]
    
    """ Smooth Forward Direction """
    
    direction_filterwidth = 20
    forward = filters.gaussian_filter1d(
        np.cross(across, np.array([[0,1,0]])), direction_filterwidth, axis=0, mode='nearest')    
    forward = forward / np.sqrt((forward**2).sum(axis=-1))[...,np.newaxis]

    root_rotation = Quaternions.between(forward, 
        np.array([[0,0,1]]).repeat(len(forward), axis=0))[:,np.newaxis] 

    """ Foot Contacts """
    
    fid_l, fid_r = np.array([4,5]), np.array([9,10])
    velfactor = np.array([0.02, 0.02])
    
    feet_l_x = (global_positions[1:,fid_l,0] - global_positions[:-1,fid_l,0])**2
    feet_l_y = (global_positions[1:,fid_l,1] - global_positions[:-1,fid_l,1])**2
    feet_l_z = (global_positions[1:,fid_l,2] - global_positions[:-1,fid_l,2])**2
    feet_l = (((feet_l_x + feet_l_y + feet_l_z) < velfactor))
    
    feet_r_x = (global_positions[1:,fid_r,0] - global_positions[:-1,fid_r,0])**2
    feet_r_y = (global_positions[1:,fid_r,1] - global_positions[:-1,fid_r,1])**2
    feet_r_z = (global_positions[1:,fid_r,2] - global_positions[:-1,fid_r,2])**2
    feet_r = (((feet_r_x + feet_r_y + feet_r_z) < velfactor))
    
    feet_l = np.concatenate([feet_l, feet_l[-1:]], axis=0)
    feet_r = np.concatenate([feet_r, feet_r[-1:]], axis=0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

②对于双脚的脚跟脚尖不同的触地状态

• 脚触地的时候,分别提取左脚跟高度与阈值高度差值、左脚尖高度与阈值高度差值、右脚跟与阈值高度差值、右脚尖与阈值高度差值

• 脚非触地状态时候, 分别提取左脚跟高度与阈值高度差值、左脚尖高度与阈值高度差值、右脚跟与阈值高度差值、右脚尖与阈值高度差值

  """ Toe and Heel Heights """
      #脚尖与脚跟的高度
      toe_h, heel_h = 4.0, 5.0
      
      """ Foot Down Positions """
      #触地的脚
      feet_down = np.concatenate([
          global_positions[feet_l[:,0],fid_l[0]] - np.array([0, heel_h, 0]),#左脚跟触地的时候
          global_positions[feet_l[:,1],fid_l[1]] - np.array([0,  toe_h, 0]),#左脚尖触地
          global_positions[feet_r[:,0],fid_r[0]] - np.array([0, heel_h, 0]),#右脚跟触地
          global_positions[feet_r[:,1],fid_r[1]] - np.array([0,  toe_h, 0])#右脚尖触地
      ], axis=0)
      
      """ Foot Up Positions """
      #不触地的脚
      feet_up = np.concatenate([
          global_positions[~feet_l[:,0],fid_l[0]] - np.array([0, heel_h, 0]),
          global_positions[~feet_l[:,1],fid_l[1]] - np.array([0,  toe_h, 0]),
          global_positions[~feet_r[:,0],fid_r[0]] - np.array([0, heel_h, 0]),
          global_positions[~feet_r[:,1],fid_r[1]] - np.array([0,  toe_h, 0])
      ], axis=0)
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21

③区分不同触地状态下的xz平面和y方向坐标值

• 脚触地的时候, 将脚的$xz$坐标提取出来$feet\_down\_xz$,将其高度值$y$提取出来$feet\_down\_y$, 分别计算其均值和方差

• 脚非触地的时候, 只需提取出脚的$xz$坐标和高度值$y$

  """ Down Locations """
      
      feet_down_xz = np.concatenate([feet_down[:,0:1], feet_down[:,2:3]], axis=-1)#触地时xz坐标
      feet_down_xz_mean = feet_down_xz.mean(axis=0)#触地时xz均值
      feet_down_y = feet_down[:,1:2]#触地时脚高度
      feet_down_y_mean = feet_down_y.mean(axis=0)#触地时高度均值
      feet_down_y_std  = feet_down_y.std(axis=0)#触地时高度方差
          
      """ Up Locations """
      #不触地时
      feet_up_xz = np.concatenate([feet_up[:,0:1], feet_up[:,2:3]], axis=-1)#脚抬起时xz位置
      feet_up_y = feet_up[:,1:2]#脚抬起时高度
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12

④计算误差函数

if len(feet_down_xz) == 0:
    
        """ No Contacts """
    	#没有触地
        terr_func = lambda Xp: np.zeros_like(Xp)[:,:1][np.newaxis].repeat(nsamples, axis=0)
        
    elif type == 'flat':
        
        """ Flat """
        #如果触地，地形高度就预设为平均高度，flat一般是弯腰过障碍物
        terr_func = lambda Xp: np.zeros_like(Xp)[:,:1][np.newaxis].repeat(nsamples, axis=0) + feet_down_y_mean
    
    else:
        
        """ Terrain Heights """
        #如果是其他情况，如跨越障碍物
        terr_down_y = patchfunc(patches, feet_down_xz - feet_down_xz_mean)#输入地形块(N,128,128)和当前脚的水平面位置，得到当前脚所在的地形快高度
        terr_down_y_mean = terr_down_y.mean(axis=1)#每个地形块对应的所有帧高度均值
        terr_down_y_std  = terr_down_y.std(axis=1)#每个地形块对应的所有帧高度方差
        terr_up_y = patchfunc(patches, feet_up_xz - feet_down_xz_mean)#得到不触地时对应的高度值
        
        """ Fitting Error """
        #触地时：零均值的平均地形高度与零均值时脚高度的差值的平方的均值，确保触地时，脚和地形高度一样
        terr_down_err = 0.1 * ((
            (terr_down_y - terr_down_y_mean[:,np.newaxis]) -
            (feet_down_y - feet_down_y_mean)[np.newaxis])**2)[...,0].mean(axis=1)
        #非触地时：零均值的平均地形高度与零均值的脚高度的差值的平方的最大值的均值，应该是高度差，确保非触地时，脚的位置高于地面
        terr_up_err = (np.maximum(
            (terr_up_y - terr_down_y_mean[:,np.newaxis]) -
            (feet_up_y - feet_down_y_mean)[np.newaxis], 0.0)**2)[...,0].mean(axis=1)
        
        """ Jumping Error """
        #跨越障碍物时
        if type == 'jumpy':
            terr_over_minh = 5.0 #障碍物最低高度
            terr_over_err = (np.maximum(
                ((feet_up_y - feet_down_y_mean)[np.newaxis] - terr_over_minh) -
                (terr_up_y - terr_down_y_mean[:,np.newaxis]), 0.0)**2)[...,0].mean(axis=1)#脚的高度与地形高度的差值不能小于障碍物的最低高度
        else:
            terr_over_err = 0.0
        
        """ Fitting Terrain to Walking on Beam """
        
        if type == 'beam':
			#上栏杆，在栏杆上走，下栏杆的运动
            beam_samples = 1
            beam_min_height = 40.0 #最低高度

            beam_c = global_positions[:,0] #根关节位置
            beam_c_xz = np.concatenate([beam_c[:,0:1], beam_c[:,2:3]], axis=-1) #根关节xz坐标
            beam_c_y = patchfunc(patches, beam_c_xz - feet_down_xz_mean) #根关节对应的地形坐标

            beam_o = (
                beam_c.repeat(beam_samples, axis=0) + np.array([50, 0, 50]) * 
                rng.normal(size=(len(beam_c)*beam_samples, 3)))#xz施加噪声后的根关节坐标

            beam_o_xz = np.concatenate([beam_o[:,0:1], beam_o[:,2:3]], axis=-1)#具有噪声的xz
            beam_o_y = patchfunc(patches, beam_o_xz - feet_down_xz_mean)#噪声xz对应的地形高度

            beam_pdist = np.sqrt(((beam_o[:,np.newaxis] - beam_c[np.newaxis,:])**2).sum(axis=-1)) #噪声使数据的偏移距离
            beam_far = (beam_pdist > 15).all(axis=1) #所有大于15的距离
			#保证当前位置和附近位置的地形高度差不小于40
            terr_beam_err = (np.maximum(beam_o_y[:,beam_far] - 
                (beam_c_y.repeat(beam_samples, axis=1)[:,beam_far] - 
                 beam_min_height), 0.0)**2)[...,0].mean(axis=1)#原始匹配的地形高度-噪声地形高度-最高高度

        else:
            terr_beam_err = 0.0
        
        """ Final Fitting Error """
        #最小化目标：
        #触地时：脚的高度与地形高度最小
        #不触地时：脚的高度应该高于地形高度
        #跨越障碍物时：教的高度与地形高度的差值要大于障碍物最低高度的5.0
        #上栏杆行走时：当前所处地形与附近的地形高度差不能小于40
        terr = terr_down_err + terr_up_err + terr_over_err + terr_beam_err
        
        """ Best Fitting Terrains """
        
        terr_ids = np.argsort(terr)[:nsamples] #依据误差排序，选10个误差最小的地形块，得到索引
        terr_patches = patches[terr_ids] #把索引块提取出来(10,128,128)
        terr_basic_func = lambda Xp: (
            (patchfunc(terr_patches, Xp - feet_down_xz_mean) - 
            terr_down_y_mean[terr_ids][:,np.newaxis]) + feet_down_y_mean)#重新在10个块中计算地形函数：地形高度-平均地形高度+脚触地的平均高度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

• 落地和抬脚时候地形与脚的误差:
  对于每一个帧段中脚落地和抬起的帧对应的轨迹位置, 在所有地形块中找到此位置对应的地形高度
  
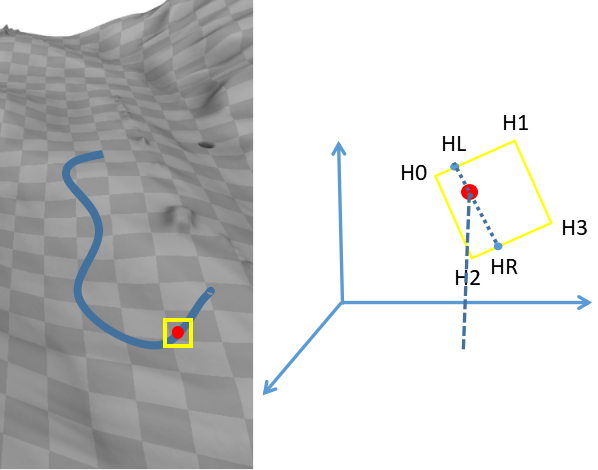
  蓝色为footsteps对应的一段运动的轨迹, 红色点对应其中某一帧, 根据此帧在$xz$平面投影坐标相邻的四个角的地形位置坐标(黄色框), 根据类似于双线性插值的方法计算出红色点位置的地形高度.由此便分别找到了帧段中脚的高度$f_i^j$,再分别计算脚抬起的时候地形与当前脚高度的误差$E_{down}$, 以及脚抬起的时候地形与脚高度的误差$E_{up}$
  $$\begin{gathered} E_{down}=\sum _i\sum _{j\in J}{c}_i^j(h_i^j-f_i^j{)}^2 \\ {E}_{up}=\sum _i\sum _{j\in J}(1-c_i^j)\max (h_i^j-f_i^j,0{)}^2 \end{gathered}$$
  其中$c_i^j$代表哪一只脚的脚尖或者是脚跟的触地状态,$h_i^j$是当前脚位置对应的地形高度(红色点),$f_i^j$对应当前帧的脚的高度, 均包含左右脚的脚跟和脚尖, 主要是为了确保脚触地的时候,脚的高度和地形高度一样, 脚不触地的时候, 脚的高度适中在地面之上

• 当运动风格为jumpy的时候的误差
  $$E_{over}=\sum _i\sum _{j\in J}{g}_j^{jump}(1-c_i^j)\max ((f_i^j-l)-h_i^j,0{)}^2$$
  其中$g_j^{jump}$是判断当前运动风格是否为$jumpy$, $l$代表地面的最低高度,文章是$l=30cm$

• 此外, 除去文章的三个误差外, 还有当运动风格为beam的时候的误差
  方法比较奇怪, 先提取原始运动的$xz$坐标, 并计算当前坐标对应的地形高度; 随后对原始运动每一帧的$xz$坐标分别加入$50\times 标准正态分布$,随后计算新的$x^{\prime }{z}^{\prime }$坐标对应的地形高度, 然后误差表示为
  E b e a m = ∑ i ∑ j ∈ J g j b e a m 1 { d i s t ( b o , b c ) > 15 } max ⁡ ( b o h i j − b c h i j − b m h , 0 ) 2 E_{beam}=\sum_i\sum_{j\in J} g_j^{beam}1\{dist(bo,bc)>15\}\max(boh_i^j-bch_i^j-bmh,0)^2 Ebeam​=i∑​j∈J∑​gjbeam​1{dist(bo,bc)>15}max(bohij​−bchij​−bmh,0)2
  其中$g_j^{beam}$代表当前运动风格是否为beam, $boh$和$bch$分别代表$xz$坐标未加噪和加噪的位置对应的地形高度, 第二项中的 $dist$代表每个当前帧$bo$与每个的加噪帧$bc$的根节点坐标平方和, 得到的是$(帧数\ast 帧数\ast 距离)$的矩阵
  d i s t ( b o , b c ) = ∑ n ∈ { x , y , z } ( b o n − b c n ) 2 dist(bo,bc)=\sum_{n\in\{x,y,z\}}(bo_n-bc_n)^2 dist(bo,bc)=n∈{x,y,z}∑​(bon​−bcn​)2
  随后只要原始运动与任意的一个加噪运动帧的根节点距离大于15, 就将索引记录在示性函数 1 { ⋅ } 1\{\cdot\} 1{⋅}中, 随后丢入到误差$E_{beam}$的计算中

  最终整个地形与运动脚高度的误差即为
  $$E=E_{down}+E_{up}+E_{over}+E_{beam}$$
  取当前帧段对应的所有地形块中误差$E$最小的$10$个地形块, 计算径向基函数线性插值所需的残差量,得到的是$10\times 帧段长\times 1$ 大小的误差矩阵
  $$Residua{l}_i=f_i-h_i^{basic}$$
  这里的基准地形高度为
  h i b a s i c = h i { 1 ⋯ 10 } − h m e a n { 1 ⋯ 10 } + f m e a n h^{basic}_i=h_i^{\{1\cdots10\}}-h_{mean}^{\{1\cdots10\}}+f_{mean} hibasic​=hi{1⋯10}​−hmean{1⋯10}​+fmean​
  其中 h i { 1 ⋯ 10 } h_i^{\{1\cdots10\}} hi{1⋯10}​ 是第$i$帧对应的十个地形块对应坐标处的高度, h m e a n { 1 ⋯ 10 } h_{mean}^{\{1\cdots10\}} hmean{1⋯10}​ 对应10个$128\times 128$大小的地形块的平均高度,$f_{mean}$ 代表当前帧段的所有帧高度的均值

  【注】以上所有的关于人体的高度$f$都包含左右脚跟和脚尖四个值

  随后将坐标为$xz$(此坐标是将当前帧段放入到地形块中以后的某帧在$xz$平面投影位置)的地形高度依据其残差量$Residua{l}_i$进行RBF地形矫正.

  三、RBF地形矫正

  """ Terrain Fit Editing """
          #地形修改，RBF矫正
          terr_residuals = feet_down_y - terr_basic_func(feet_down_xz)
          terr_fine_func = [RBF(smooth=0.1, function='linear') for _ in range(nsamples)]
          for i in range(nsamples): terr_fine_func[i].fit(feet_down_xz, terr_residuals[i])
          terr_func = lambda Xp: (terr_basic_func(Xp) + np.array([ff(Xp) for ff in terr_fine_func]))
  1
  2
  3
  4
  5
  6

  输入是当前运动的轨迹位置($xz$坐标), 以及当前地形块(共$10$个)对应的轨迹所有坐标点的残差量向量, 先使用$X$自身的距离矩阵$D$(每一个位置与其它位置的距离), 经过核函数得到平滑系数:
  $$K\left(\frac{1}{D_{mean}}\ast D\right)$$
  当核函数是处理多重二次曲面(multiquadric)的时候, 表达式为
  $$K(x)=\sqrt{x^2+1}$$
  然后利用LU factorization with pivoting分解此平滑系数得到拟合系数
  $$A=LU\left(K\left(\frac{D}{D_{mean}}\right)-smooth\right)$$
  随后解方程$A\ast x=Residual$即可得到修正高度$\nabla T$
  $$\nabla T=x\ast K\left(\frac{D}{D_{mean}}\right)$$
  最终的地形高度即为:
  $$T=h^{basic}+\nabla T$$
  分别提取十个地形块对应每帧位置及其左右各$25cm$处的地形高度$T_c,T_l,T_r$ , 维度均为$10\ast 帧数$

  四、帧块的地形高度

  """ Get Trajectory Terrain Heights """
      #根关节位置以及左右各25距离的位置
      root_offsets_c = global_positions[:,0] #根关节位置
      root_offsets_r = (-root_rotation[:,0] * np.array([[+25, 0, 0]])) + root_offsets_c #根关节左边25位置
      root_offsets_l = (-root_rotation[:,0] * np.array([[-25, 0, 0]])) + root_offsets_c#根关节右边25位置
  
      root_heights_c = terr_func(root_offsets_c[:,np.array([0,2])])[...,0]#根关节位置损失，每帧都有10个对应地形
      root_heights_r = terr_func(root_offsets_r[:,np.array([0,2])])[...,0]#左损失
      root_heights_l = terr_func(root_offsets_l[:,np.array([0,2])])[...,0]#右损失
      
      """ Find Trajectory Heights at each Window """
      
      root_terrains = []
      root_averages = []
      for i in range(window, len(anim)-window, 1): #从第60帧开始
          root_terrains.append(
              np.concatenate([
                  root_heights_r[:,i-window:i+window:10],
                  root_heights_c[:,i-window:i+window:10],
                  root_heights_l[:,i-window:i+window:10]], axis=1)) #拼接120帧的左中右高度，最终得到10*36的矩阵，10是地形块个数，36是12帧的左中右3个地形高度
          root_averages.append(root_heights_c[:,i-window:i+window:10].mean(axis=1))#中间帧的平均地形高度
       
      root_terrains = np.swapaxes(np.array(root_terrains), 0, 1)#交换一下维度10*N*36，N代表能滑动多少次窗口
      root_averages = np.swapaxes(np.array(root_averages), 0, 1)#平均地形高度10*N
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24

  对整个帧块从第$60$帧开始按照$120$帧块大小(被下采样为12帧)一直到倒数第$60$帧为止, 每一帧块进行左中右三个位置地形高度的提取以及当前中间位置地形高度的均值信息, 如此得到10个地形中共$len(footsteps.txt)-12$个12帧块轨迹对应的的三个地形(左中右)高度信息, 维度为$10\ast 帧块数\ast 36$的地形数据信息以及$10\ast 帧块数\ast 1$的均值高度信息

  模型输入关于地形部分维度(36维)详情:

    """For each Locomotion Cycle fit Terrains"""
      # 对每个运动矫正其地形
    for li in range(len(footsteps)-1):
      
          curr, next = footsteps[li+0].split(' '), footsteps[li+1].split(' ')
        
          """ Ignore Cycles marked with '*' or not in range """
        
          if len(curr) == 3 and curr[2].strip().endswith('*'): continue
          if len(next) == 3 and next[2].strip().endswith('*'): continue
          if len(next) <  2: continue
          if int(curr[0])//2-window < 0: continue
          if int(next[0])//2-window >= len(Xc): continue 
          
          """ Fit Heightmaps """
          
          slc = slice(int(curr[0])//2-window, int(next[0])//2-window+1)
          #H:10*N*36代表10个地形块的N帧附近12帧左中右的3个地形高度
          #H：10*N代表10个地形块，每帧附近12帧的地形高度均值
          H, Hmean = process_heights(anim[
              int(curr[0])//2-window:
              int(next[0])//2+window+1], type=type) #选中一个运动片段粗粒高度
  
          for h, hmean in zip(H, Hmean):
              
              Xh, Yh = Xc[slc].copy(), Yc[slc].copy()#Xc代表输入，Yc代表输出
              
              """ Reduce Heights in Input/Output to Match"""
              
              xo_s, xo_e = ((window*2)//10)*10+1, ((window*2)//10)*10+njoints*3+1 #121帧，121帧+关节数*3+1=214
              yo_s, yo_e = 8+(window//10)*4+1, 8+(window//10)*4+njoints*3+1#22，126
              #下面python都是从0索引，上面关于Xc和Yc的注释都是从1索引
              Xh[:,xo_s:xo_e:3] -= hmean[...,np.newaxis]#输入的121维度至214维度是当前关节的局部位置和局部速度，将他们的y坐标都减去地形均值
              Yh[:,yo_s:yo_e:3] -= hmean[...,np.newaxis]#输出的33值126是下一帧局部位置信息，将他们的坐标都减去地形均值
              Xh = np.concatenate([Xh, h - hmean[...,np.newaxis]], axis=-1)#地形零均值化，并与Xc进行高度处理后的Xh拼接306+36=342
              
              """ Append to Data """
              
              P.append(np.hstack([0.0, Pc[slc][1:-1], 1.0]).astype(np.float32))
              X.append(Xh.astype(np.float32))
              Y.append(Yh.astype(np.float32))
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26
  27
  28
  29
  30
  31
  32
  33
  34
  35
  36
  37
  38
  39
  40
  41

  先对预处理过的数据集依据footsteps.txt文件进行裁剪选取帧段, 随后进行如下操作

  直接利用地形均值高度信息对模型输入中关于人体部分的关节局部位置(从121~214维度)的y坐标与整个帧段的人体高度的均值做差, 随后将去均值化后的地形高度拼接到输入向量中, 因而输入数据的变化为:

  • 帧窗口关节位置的局部坐标(第121~213维)的$y$坐标进行去均值处理
  • 帧窗口对应的地形高度信息: 共12帧, 每帧中间及其左右$25cm$处的地形高度维度$12\ast 3=36$

  模型输入的总维度为$306+36=342$

  模型输出的总维度为$311$

模型输入输出总结

最终的输入数据每帧的维度为$342$, 输出数据的每帧维度为$311$, 帧总数即为footsteps.txt中标注的帧段信息的第一行和最后一行, 只不过每次处理是依据相邻两行索引的帧段进行地形的搜索和编辑.

所有运动文件综合起来, 得到的最终丢给模型训练的数据量为:

输入维度:$(4353570L,342L)$

相位维度:$(4353570L,1L)$

输出维度: $(4353570L,311L)$

最终的模型输入Xun:342维

1-12:所有帧根关节的x坐标
13-24:所有帧根关节的z坐标
25-36:所有帧根关节的x方向
37-48:所有帧根关节的z方向
49-120:所有帧6种步态参数12*6
121-213:当前关节的局部位置，注意高度已经减去了地形均值 31*3=93
214-306:当前关节的局部速度31*3
301-342:当前关节附近12帧(已下采样10间隔)的左中右地形高度 12*3=36
1
2
3
4
5
6
7
8

最终模型输出：311维

1:根关节x方向移动速度
2:根关节y方向移动速度
3:根关节旋转速度
4:相位值变化量
5-8:当前帧左右脚跟脚尖触地状况
9-20：未来6帧关节xz位置变化量
21-32：未来6帧根关节xz方向变化量
33-125：当前31个关节局部位置信息
126-218：当前帧31个关节局部速度信息
219-311：当前帧31个关节局部旋转信息，是全局旋转矩阵
1
2
3
4
5
6
7
8
9
10

P：相位值

模型

模型结构

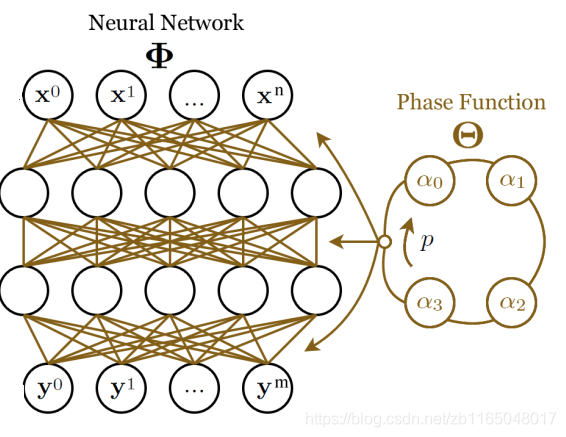
整个模型的结构较为简单, 输入单元数为$342$, 输出单元数为$311$, 中间两个隐层的维度均为$512$

训练方法

正式进入训练阶段

train_pfnn.py是主要的训练文件

nn/AdamTrainer.py是优化器

数据与处理

database = np.load('database.npz') #读数据
X = database['Xun'].astype(theano.config.floatX) #4353570*342输入
Y = database['Yun'].astype(theano.config.floatX) #4353570*311输出
P = database['Pun'].astype(theano.config.floatX) #4353570*1原始相位

print(X.shape, Y.shape)

""" Calculate Mean and Std """
# 计算训练集的均值和方差
Xmean, Xstd = X.mean(axis=0), X.std(axis=0)
Ymean, Ystd = Y.mean(axis=0), Y.std(axis=0)

j = 31 #关节数目
w = ((60*2)//10) #窗口大小12
#针对每部分不同的内容再求均值和方差
Xstd[w*0:w* 1] = Xstd[w*0:w* 1].mean() # Trajectory Past Positions过去帧的位置1-12
Xstd[w*1:w* 2] = Xstd[w*1:w* 2].mean() # Trajectory Future Positions将来帧的位置13-24
Xstd[w*2:w* 3] = Xstd[w*2:w* 3].mean() # Trajectory Past Directions过去帧的方向25-36
Xstd[w*3:w* 4] = Xstd[w*3:w* 4].mean() # Trajectory Future Directions将来帧的方向37-48
Xstd[w*4:w*10] = Xstd[w*4:w*10].mean() # Trajectory Gait 帧片段的步态 49-120

""" Mask Out Unused Joints in Input """

joint_weights = np.array([
    1,
    1e-10, 1, 1, 1, 1,
    1e-10, 1, 1, 1, 1,
    1e-10, 1, 1,
    1e-10, 1, 1,
    1e-10, 1, 1, 1, 1e-10, 1e-10, 1e-10,
    1e-10, 1, 1, 1, 1e-10, 1e-10, 1e-10]).repeat(3) #关节权重

Xstd[w*10+j*3*0:w*10+j*3*1] = Xstd[w*10+j*3*0:w*10+j*3*1].mean() / (joint_weights * 0.1) # Pos 当前关节的局部位置121-213
Xstd[w*10+j*3*1:w*10+j*3*2] = Xstd[w*10+j*3*1:w*10+j*3*2].mean() / (joint_weights * 0.1) # Vel 当前关节的局部速度214-306
Xstd[w*10+j*3*2:          ] = Xstd[w*10+j*3*2:          ].mean() # Terrain 附近12帧左中右的地形高度307-342
#对输出再进行均值处理
Ystd[0:2] = Ystd[0:2].mean() # Translational Velocity
Ystd[2:3] = Ystd[2:3].mean() # Rotational Velocity
Ystd[3:4] = Ystd[3:4].mean() # Change in Phase
Ystd[4:8] = Ystd[4:8].mean() # Contacts

Ystd[8+w*0:8+w*1] = Ystd[8+w*0:8+w*1].mean() # Trajectory Future Positions
Ystd[8+w*1:8+w*2] = Ystd[8+w*1:8+w*2].mean() # Trajectory Future Directions

Ystd[8+w*2+j*3*0:8+w*2+j*3*1] = Ystd[8+w*2+j*3*0:8+w*2+j*3*1].mean() # Pos
Ystd[8+w*2+j*3*1:8+w*2+j*3*2] = Ystd[8+w*2+j*3*1:8+w*2+j*3*2].mean() # Vel
Ystd[8+w*2+j*3*2:8+w*2+j*3*3] = Ystd[8+w*2+j*3*2:8+w*2+j*3*3].mean() # Rot

""" Save Mean / Std / Min / Max """

Xmean.astype(np.float32).tofile('./demo/network/pfnn/Xmean.bin')
Ymean.astype(np.float32).tofile('./demo/network/pfnn/Ymean.bin')
Xstd.astype(np.float32).tofile('./demo/network/pfnn/Xstd.bin')
Ystd.astype(np.float32).tofile('./demo/network/pfnn/Ystd.bin')

""" Normalize Data """

X = (X - Xmean) / Xstd
Y = (Y - Ymean) / Ystd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

先读取整个数据集, 然后对不同意义上的维度分别归一化, 分别包含

输入数据的(除了121~306仅包含一帧信息外, 其它数据均包含左右相邻共12帧信息):

• 所有帧x坐标: 1~12
• 所有帧z坐标:13~24
• 所有帧x方向: 25~36
• 所有帧z方向: 37~48
• 所有帧6种步态参数: 49~120
• 所有帧中间帧姿态: 121~213(注意关节权重的设置)
• 所有帧中间帧方向: 214~306(注意关节权重的设置)
• 所有帧地形高度与轨迹均值做差: 307~342

输出数据的:

• 根关节$xz$移动速度: 1~2
• 根关节绕竖直轴旋转速度: 3
• 相位值: 4
• 触地信息: 5~8
• 未来6帧根关节$xz$位置: 9~20(相对于第一帧)
• 未来6帧根关节$xz$方向: 21~32(对于第一帧)
• 当前帧31个关节坐标: 33~125
• 当前帧31个关节速度:126~218
• 当前帧31个关节旋转:218~311

前向计算

与文章对应, 利用相位值函数phase function计算动态权重, 文章采用Cubic Catmull-Rom spline function, 具有四个控制点, 具体的前向计算方法如下:

def __call__(self, input):
        #公式的动态权重
        pscale = self.nslices * input[:,-1] #公式中的4p，其中4是nslices,input[:,-1]就是相位p
        pamount = pscale % 1.0 #与1.0取余
        
        pindex_1 = T.cast(pscale, 'int32') % self.nslices #公式里的k1=4p%4
        pindex_0 = (pindex_1-1) % self.nslices #公式k0
        pindex_2 = (pindex_1+1) % self.nslices #公式k2
        pindex_3 = (pindex_1+2) % self.nslices #公式k3
        
        Wamount = pamount.dimshuffle(0, 'x', 'x')
        bamount = pamount.dimshuffle(0, 'x')
        
        def cubic(y0, y1, y2, y3, mu):
            return (
                (-0.5*y0+1.5*y1-1.5*y2+0.5*y3)*mu*mu*mu + 
                (y0-2.5*y1+2.0*y2-0.5*y3)*mu*mu + 
                (-0.5*y0+0.5*y2)*mu +
                (y1))
        #利用公式7分别计算权重
        W0 = cubic(self.W0.W[pindex_0], self.W0.W[pindex_1], self.W0.W[pindex_2], self.W0.W[pindex_3], Wamount)
        W1 = cubic(self.W1.W[pindex_0], self.W1.W[pindex_1], self.W1.W[pindex_2], self.W1.W[pindex_3], Wamount)
        W2 = cubic(self.W2.W[pindex_0], self.W2.W[pindex_1], self.W2.W[pindex_2], self.W2.W[pindex_3], Wamount)
        #利用公式7分别计算偏置
        b0 = cubic(self.b0.b[pindex_0], self.b0.b[pindex_1], self.b0.b[pindex_2], self.b0.b[pindex_3], bamount)
        b1 = cubic(self.b1.b[pindex_0], self.b1.b[pindex_1], self.b1.b[pindex_2], self.b1.b[pindex_3], bamount)
        b2 = cubic(self.b2.b[pindex_0], self.b2.b[pindex_1], self.b2.b[pindex_2], self.b2.b[pindex_3], bamount)
        #前向计算
        H0 = input[:,:-1]
        H1 = self.activation(T.batched_dot(W0, self.dropout0(H0)) + b0)
        H2 = self.activation(T.batched_dot(W1, self.dropout1(H1)) + b1)
        H3 =                 T.batched_dot(W2, self.dropout2(H2)) + b2
        
        return H3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

首先初始化各层权重矩阵:

• 输入$\to$第一隐层,维度: $4\times 512\times 342$, 记为$W_0$
• 第一隐层$\to$第二隐层, 维度:$4\times 512\times 512$, 记为$W_1$
• 第二隐层$\to$输出层,维度: $4\times 311\times 512$,记为$W_2$
• 各层(除第一层)偏置$b_0,b_1,b_2$

随后使用phase function, 利用四个控制点计算动态权重
W = α k 1 + μ ( − 1 2 α k 0 + 1 2 α k 2 ) + μ 2 ( α k 0 − 5 2 α k 1 + 2 α k 2 − 1 2 α k 3 ) + μ 3 ( − 1 2 α k 0 + 3 2 α k 1 − 1 2 α k 2 + 1 2 α k 3 )

$$\begin{aligned} W&= \alpha_{k_1}\\ &+\mu(-\frac{1}{2}\alpha_{k_0}+\frac{1}{2}\alpha_{k_2})\\ &+\mu^2(\alpha_{k_0}-\frac{5}{2}\alpha_{k_1}+2\alpha_{k_2}-\frac{1}{2}\alpha_{k_3})\\ &+\mu^3(-\frac{1}{2}\alpha_{k_0}+\frac{3}{2}\alpha_{k_1}-\frac{1}{2}\alpha_{k_2}+\frac{1}{2}\alpha_{k_3})\\ \end{aligned}$$ W​=αk1​​+μ(−21​αk0​​+21​αk2​​)+μ2(αk0​​−25​αk1​​+2αk2​​−21​αk3​​)+μ3(−21​αk0​​+23​αk1​​−21​αk2​​+21​αk3​​)​

对每一层权重矩阵都利用上式进行更新, 在上式中, ${\alpha }_k$代表当前权重的第一维度的第$k$个索引, 比如对于$W0$,${\alpha }_{k_0}=W0[k_0]$, 而索引的计算方法是
$$k_n=(4p+n-1)mod4$$
对于系数$\mu$的计算方法是
$$\mu =(4p)mod1$$
其实这样做的操作主要是$p$为包含小数的连续数值, 这样取余有助于得到小数部分的数值, 同时保持平滑性, 但是这里的计算与原文不同, 原文对$k_n,\mu$的计算均除以$2\pi$了, 据此推测原始的phase文件记录的值已经被处理过

由此可以推测出前向计算(重构运动)的过程:
$$\Phi (x;W)=W_{2}ELU(W_{1}ELU(W_{0}x+b_0)+b_1)+b_2$$
上式中的$W$均值被phase function处理过的值, 其中ELU是激活函数,表达式为
$$ELU(x)=\max (x,0)+\exp (\min (x,0))-1$$

梯度更新

进入AdamTrainer.py中，第$27$行代码：

    def get_cost_updates(self, network, input, output):
        
        cost = self.cost(network, input, output) + network.cost(input)
        #cost = self.cost(network, input, output)
        
        gparams = T.grad(cost, self.params)
        m0params = [self.beta1 * m0p + (1-self.beta1) *  gp     for m0p, gp in zip(self.m0params, gparams)]
        m1params = [self.beta2 * m1p + (1-self.beta2) * (gp*gp) for m1p, gp in zip(self.m1params, gparams)]
        params = [p - self.alpha * 
                  ((m0p/(1-(self.beta1**self.t[0]))) /
            (T.sqrt(m1p/(1-(self.beta2**self.t[0]))) + self.eps))
            for p, m0p, m1p in zip(self.params, m0params, m1params)]
        
        updates = ([( p,  pn) for  p,  pn in zip(self.params, params)] +
                   [(m0, m0n) for m0, m0n in zip(self.m0params, m0params)] +
                   [(m1, m1n) for m1, m1n in zip(self.m1params, m1params)] +
                   [(self.t, self.t+1)])

        return (cost, updates)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

先定义目标函数=MSE损失函数+正则项:
$$L=\parallel Y-O{\parallel }_2^2+\gamma |\beta |$$
更新方法采用Adam优化算法:
m t = β 1 m t − 1 + ( 1 − β 1 ) g t v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 m t ^ = m t 1 − β 1 t v t ^ = v t 1 − β 2 t θ t + 1 = θ t − η ⋅ m t ^ v t ^ + ϵ

$$\begin{aligned} m_t&=\beta_1m_{t-1}+(1-\beta_1)g_t\\ v_t&=\beta_2v_{t-1}+(1-\beta_2)g_t^2\\ \hat{m_t}&=\frac{m_t}{1-\beta_1^t}\\ \hat{v_t}&=\frac{v_t}{1-\beta_2^t}\\ \theta_{t+1}&=\theta_t-\eta\cdot\frac{\hat{m_t}}{\sqrt{\hat{v_t}}+\epsilon} \end{aligned}$$ mt​vt​mt​^​vt​^​θt+1​​=β1​mt−1​+(1−β1​)gt​=β2​vt−1​+(1−β2​)gt2​=1−β1t​mt​​=1−β2t​vt​​=θt​−η⋅vt​^​ ​+ϵmt​^​​​
初始时刻$m0params=0,m1params=0,{\beta }_1=0.9,{\beta }_2=0.999,ϵ=10^{-8}$

迭代 处理及模型保存

先将整个数据集划分为10个批次, 然后对每个批次划分小批训练,每小批大小16, 对于每小批训练100次, 整个过程循环二十次,每次的10个大批次都是从整体样本中随机选的一段, 但是所有的合起来是整个样本.

考虑到模型训练完毕以后, 权重和偏置参数基本固定, 唯一耗时的是利用phase function利用四个控制点做动态权重更新, 考虑到相位值的变化范围有限$(0\to 1or2\pi )$, 因而可以预先计算好一些不同间隔的相位函数值, 从而减少运行时间效率. 因而出现了文章运行时所需要的模型参数, 保存了$0\to 1$中$50$个间隔的相位函数计算得到的参数(权重和偏置)值.

def save_network(network):

    """ Load Control Points """

    W0n = network.W0.W.get_value()
    W1n = network.W1.W.get_value()
    W2n = network.W2.W.get_value()

    b0n = network.b0.b.get_value()
    b1n = network.b1.b.get_value()
    b2n = network.b2.b.get_value()
    
    """ Precompute Phase Function """
    
    for i in range(50): #保存50个值
        
        pscale = network.nslices*(float(i)/50) #50个相位值
        pamount = pscale % 1.0
        
        pindex_1 = int(pscale) % network.nslices
        pindex_0 = (pindex_1-1) % network.nslices
        pindex_2 = (pindex_1+1) % network.nslices
        pindex_3 = (pindex_1+2) % network.nslices
        
        def cubic(y0, y1, y2, y3, mu):
            return (
                (-0.5*y0+1.5*y1-1.5*y2+0.5*y3)*mu*mu*mu + 
                (y0-2.5*y1+2.0*y2-0.5*y3)*mu*mu + 
                (-0.5*y0+0.5*y2)*mu +
                (y1))
        
        W0 = cubic(W0n[pindex_0], W0n[pindex_1], W0n[pindex_2], W0n[pindex_3], pamount)
        W1 = cubic(W1n[pindex_0], W1n[pindex_1], W1n[pindex_2], W1n[pindex_3], pamount)
        W2 = cubic(W2n[pindex_0], W2n[pindex_1], W2n[pindex_2], W2n[pindex_3], pamount)
        
        b0 = cubic(b0n[pindex_0], b0n[pindex_1], b0n[pindex_2], b0n[pindex_3], pamount)
        b1 = cubic(b1n[pindex_0], b1n[pindex_1], b1n[pindex_2], b1n[pindex_3], pamount)
        b2 = cubic(b2n[pindex_0], b2n[pindex_1], b2n[pindex_2], b2n[pindex_3], pamount)
        
        W0.astype(np.float32).tofile('./demo/network/pfnn/W0_%03i.bin' % i)
        W1.astype(np.float32).tofile('./demo/network/pfnn/W1_%03i.bin' % i)
        W2.astype(np.float32).tofile('./demo/network/pfnn/W2_%03i.bin' % i)
        
        b0.astype(np.float32).tofile('./demo/network/pfnn/b0_%03i.bin' % i)
        b1.astype(np.float32).tofile('./demo/network/pfnn/b1_%03i.bin' % i)
        b2.astype(np.float32).tofile('./demo/network/pfnn/b2_%03i.bin' % i)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

运行时

进入代码的demo/pfnn.cpp

键盘控制信息

手柄结构如下, 其中我们使用到的只有

• 左右触发器用于调整相机远近(接口参数6,7)
• 左右按钮用于调整人体朝向和运动风格(接口参数4,5)
• 左摇杆用于控制运动轨迹(接口参数8,9)
• 下摇杆用于调整相机的俯仰和偏航程度(接口参数2,3)
• B按钮用于调整直立还是弯腰(接口参数1)

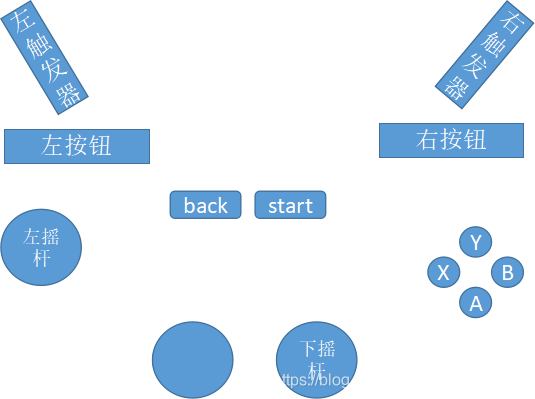
需要注意的是,摇杆和按钮是具有不同的控制功能, 因为摇杆有偏转程度, 而按钮只有按下或者不按下两种状态, 所以左右触发器, 摇杆都是axis属性获取其值, 而左右按钮和B按钮是button属性获取其值

权重初始化

第2663-2666行初始化了一个PFNN对象，随后load权重

 pfnn = new PFNN(PFNN::MODE_CONSTANT); #直接读取已计算好的50个权重
  //pfnn = new PFNN(PFNN::MODE_CUBIC); #读取4个权重，使用公式7计算动态权重
  //pfnn = new PFNN(PFNN::MODE_LINEAR); #线性计算4动态权重
  pfnn->load();
1
2
3
4

当采用CONSTANT模式时：

• 读取权重方法是一次性把50次预先计算好的权重载入：

  for (int i = 0; i < 50; i++) {            
            load_weights(W0[i], HDIM, XDIM, "./network/pfnn/W0_%03i.bin", i);
            load_weights(W1[i], HDIM, HDIM, "./network/pfnn/W1_%03i.bin", i);
            load_weights(W2[i], YDIM, HDIM, "./network/pfnn/W2_%03i.bin", i);
            load_weights(b0[i], HDIM, "./network/pfnn/b0_%03i.bin", i);
            load_weights(b1[i], HDIM, "./network/pfnn/b1_%03i.bin", i);
            load_weights(b2[i], YDIM, "./network/pfnn/b2_%03i.bin", i);            
          }
  1
  2
  3
  4
  5
  6
  7
  8

• 预测阶段直接前向计算：

  pindex_1 = (int)((P / (2*M_PI)) * 50);
          H0 = (W0[pindex_1].matrix() * Xp.matrix()).array() + b0[pindex_1]; ELU(H0);
          H1 = (W1[pindex_1].matrix() * H0.matrix()).array() + b1[pindex_1]; ELU(H1);
          Yp = (W2[pindex_1].matrix() * H1.matrix()).array() + b2[pindex_1];
  1
  2
  3
  4

当采用LINEAR方法载入权重时：

• 读取权重方法是预先读取10组权重，间隔5是因为0-50被分为10组就是间隔为5

  for (int i = 0; i < 10; i++) {
            load_weights(W0[i], HDIM, XDIM, "./network/pfnn/W0_%03i.bin", i * 5);
            load_weights(W1[i], HDIM, HDIM, "./network/pfnn/W1_%03i.bin", i * 5);
            load_weights(W2[i], YDIM, HDIM, "./network/pfnn/W2_%03i.bin", i * 5);
            load_weights(b0[i], HDIM, "./network/pfnn/b0_%03i.bin", i * 5);
            load_weights(b1[i], HDIM, "./network/pfnn/b1_%03i.bin", i * 5);
            load_weights(b2[i], YDIM, "./network/pfnn/b2_%03i.bin", i * 5);  
          }
  1
  2
  3
  4
  5
  6
  7
  8

• 预测阶段使用现行函数计算动态权重

  pamount = fmod((P / (2*M_PI)) * 10, 1.0);
  pindex_1 = (int)((P / (2*M_PI)) * 10);
  pindex_2 = ((pindex_1+1) % 10);
  linear(W0p, W0[pindex_1], W0[pindex_2], pamount);
  linear(W1p, W1[pindex_1], W1[pindex_2], pamount);
  linear(W2p, W2[pindex_1], W2[pindex_2], pamount);
  linear(b0p, b0[pindex_1], b0[pindex_2], pamount);
  linear(b1p, b1[pindex_1], b1[pindex_2], pamount);
  linear(b2p, b2[pindex_1], b2[pindex_2], pamount);
  H0 = (W0p.matrix() * Xp.matrix()).array() + b0p; ELU(H0);
  H1 = (W1p.matrix() * H0.matrix()).array() + b1p; ELU(H1);
  Yp = (W2p.matrix() * H1.matrix()).array() + b2p;
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12

当采用cubic方法载入权重时：

• 读取权重阶段，只需要读4组，代表4个控制点，0-50分4组，间隔就是12.5

  for (int i = 0; i < 4; i++) {
            load_weights(W0[i], HDIM, XDIM, "./network/pfnn/W0_%03i.bin", (int)(i * 12.5));
            load_weights(W1[i], HDIM, HDIM, "./network/pfnn/W1_%03i.bin", (int)(i * 12.5));
            load_weights(W2[i], YDIM, HDIM, "./network/pfnn/W2_%03i.bin", (int)(i * 12.5));
            load_weights(b0[i], HDIM, "./network/pfnn/b0_%03i.bin", (int)(i * 12.5));
            load_weights(b1[i], HDIM, "./network/pfnn/b1_%03i.bin", (int)(i * 12.5));
            load_weights(b2[i], YDIM, "./network/pfnn/b2_%03i.bin", (int)(i * 12.5));  
          }
  1
  2
  3
  4
  5
  6
  7
  8

• 前向计算阶段，需要使用cubic函数重新计算权重

  pamount = fmod((P / (2*M_PI)) * 4, 1.0);
          pindex_1 = (int)((P / (2*M_PI)) * 4);
          pindex_0 = ((pindex_1+3) % 4);
          pindex_2 = ((pindex_1+1) % 4);
          pindex_3 = ((pindex_1+2) % 4);
          cubic(W0p, W0[pindex_0], W0[pindex_1], W0[pindex_2], W0[pindex_3], pamount);
          cubic(W1p, W1[pindex_0], W1[pindex_1], W1[pindex_2], W1[pindex_3], pamount);
          cubic(W2p, W2[pindex_0], W2[pindex_1], W2[pindex_2], W2[pindex_3], pamount);
          cubic(b0p, b0[pindex_0], b0[pindex_1], b0[pindex_2], b0[pindex_3], pamount);
          cubic(b1p, b1[pindex_0], b1[pindex_1], b1[pindex_2], b1[pindex_3], pamount);
          cubic(b2p, b2[pindex_0], b2[pindex_1], b2[pindex_2], b2[pindex_3], pamount);
          H0 = (W0p.matrix() * Xp.matrix()).array() + b0p; ELU(H0);
          H1 = (W1p.matrix() * H0.matrix()).array() + b1p; ELU(H1);
          Yp = (W2p.matrix() * H1.matrix()).array() + b2p;
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14

姿态初始化

在pfnn.cpp的第1035行rest函数中

ArrayXf Yp = pfnn->Ymean;

  glm::vec3 root_position = glm::vec3(position.x, heightmap->sample(position), position.y);
  glm::mat3 root_rotation = glm::mat3();
  
  for (int i = 0; i < Trajectory::LENGTH; i++) {
    trajectory->positions[i] = root_position;
    trajectory->rotations[i] = root_rotation;
    trajectory->directions[i] = glm::vec3(0,0,1);
    trajectory->heights[i] = root_position.y;
    trajectory->gait_stand[i] = 0.0;
    trajectory->gait_walk[i] = 0.0;
    trajectory->gait_jog[i] = 0.0;
    trajectory->gait_crouch[i] = 0.0;
    trajectory->gait_jump[i] = 0.0;
    trajectory->gait_bump[i] = 0.0;
  }
  
  for (int i = 0; i < Character::JOINT_NUM; i++) {
    
    int opos = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*0);
    int ovel = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*1);
    int orot = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*2);
    
    glm::vec3 pos = (root_rotation * glm::vec3(Yp(opos+i*3+0), Yp(opos+i*3+1), Yp(opos+i*3+2))) + root_position;
    glm::vec3 vel = (root_rotation * glm::vec3(Yp(ovel+i*3+0), Yp(ovel+i*3+1), Yp(ovel+i*3+2)));
    glm::mat3 rot = (root_rotation * glm::toMat3(quat_exp(glm::vec3(Yp(orot+i*3+0), Yp(orot+i*3+1), Yp(orot+i*3+2)))));
    
    character->joint_positions[i]  = pos;
    character->joint_velocities[i] = vel;
    character->joint_rotations[i]  = rot;
  }
  
  character->phase = 0.0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

在刚载入场景地形时,也赋予了人体基本初始姿态(总共是初始化了120帧的帧窗口):

• 轨迹位置positions: (横坐标,地形高度,纵坐标), 其实横纵坐标刚开始的时候是地形(0,0)位置
• 轨迹旋转rotations: 旋转矩阵$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$
• 轨迹方向directions: z轴正方向$(0,0,1)$
• 地形高度heights: 根关节的y轴信息
• 六种步态: 全部初始化为$0$
• 当前帧的相位值是0

依据训练集的均值作为网络输出初始化当前帧人体信息,包含:

• 相对于根关节的位置: 据此乘以旋转矩阵加上根关节坐标得到全局位置
• 沿轨迹方向的速度
• 沿轨迹方向的旋转矩阵: 初始旋转量$\times$ 网络输出的旋转量

最终得到每个关节的位置,速度,旋转矩阵

可以看出每个帧数据都是根据网络输出计算而来, 因而后面的人体关节全局坐标的获取对于场景初始化和gamepad控制都适用

网络输入/推导/输出

代码pfnn.cpp的第1423行的pre_render()函数中

先看看怎么从gamepad的控制上更新走跑速度和运动时面向方向的(注意，面向方向与运动方向是独立的，比如倒着跑)

/* Update Camera */
  //鼠标滚轮拉近和拉远摄像头
  int x_move = SDL_JoystickGetAxis(stick, GAMEPAD_STICK_R_HORIZONTAL);
  int y_move = SDL_JoystickGetAxis(stick, GAMEPAD_STICK_R_VERTICAL);
  
  if (abs(x_move) + abs(y_move) < 10000) { x_move = 0; y_move = 0; };
  
  if (options->invert_y) { y_move = -y_move; }
  
  camera->pitch = glm::clamp(camera->pitch + (y_move / 32768.0) * 0.03, M_PI/16, 2*M_PI/5);
  camera->yaw = camera->yaw + (x_move / 32768.0) * 0.03;
  
  float zoom_i = SDL_JoystickGetButton(stick, GAMEPAD_SHOULDER_L) * 20.0;
  float zoom_o = SDL_JoystickGetButton(stick, GAMEPAD_SHOULDER_R) * 20.0;
  
  if (zoom_i > 1e-5) { camera->distance = glm::clamp(camera->distance + zoom_i, 10.0f, 10000.0f); }
  if (zoom_o > 1e-5) { camera->distance = glm::clamp(camera->distance - zoom_o, 10.0f, 10000.0f); }
        
  /* Update Target Direction / Velocity */
  //更新目标方向和速度
  int x_vel = -SDL_JoystickGetAxis(stick, GAMEPAD_STICK_L_HORIZONTAL);//左右移动
  int y_vel = -SDL_JoystickGetAxis(stick, GAMEPAD_STICK_L_VERTICAL); //前后移动
  if (abs(x_vel) + abs(y_vel) < 10000) { x_vel = 0; y_vel = 0; }; 
  
  glm::vec3 trajectory_target_direction_new = glm::normalize(glm::vec3(camera->direction().x, 0.0, camera->direction().z));//相机位置
  glm::mat3 trajectory_target_rotation = glm::mat3(glm::rotate(atan2f(
    trajectory_target_direction_new.x,
    trajectory_target_direction_new.z), glm::vec3(0,1,0))); //相机方向，后面人体朝向会在轨迹方向和相机方向范围内偏转
  
  float target_vel_speed = 2.5 + 2.5 * ((SDL_JoystickGetAxis(stick, GAMEPAD_TRIGGER_R) / 32768.0) + 1.0); //移动速度
  
  glm::vec3 trajectory_target_velocity_new = target_vel_speed * (trajectory_target_rotation * glm::vec3(x_vel / 32768.0, 0, y_vel / 32768.0));
  trajectory->target_vel = glm::mix(trajectory->target_vel, trajectory_target_velocity_new, options->extra_velocity_smooth);//平滑过渡到设置的方向
  //面向方向
  character->strafe_target = ((SDL_JoystickGetAxis(stick, GAMEPAD_TRIGGER_L) / 32768.0) + 1.0) / 2.0;
  character->strafe_amount = glm::mix(character->strafe_amount, character->strafe_target, options->extra_strafe_smooth);
  
  glm::vec3 trajectory_target_velocity_dir = glm::length(trajectory->target_vel) < 1e-05 ? trajectory->target_dir : glm::normalize(trajectory->target_vel);
//面向轨迹方向还是相机方向，strafe_amount控制面向的偏转程度
  trajectory_target_direction_new = mix_directions(trajectory_target_velocity_dir, trajectory_target_direction_new, character->strafe_amount);  
  trajectory->target_dir = mix_directions(trajectory->target_dir, trajectory_target_direction_new, options->extra_direction_smooth);  //平滑上一帧与当前帧方向
  
  character->crouched_amount = glm::mix(character->crouched_amount, character->crouched_target, options->extra_crouched_smooth); //弯腰
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

再看看步态的更新

  /* Update Gait */
  
  if (glm::length(trajectory->target_vel) < 0.1)  {
      //速度太慢，就站立
    float stand_amount = 1.0f - glm::clamp(glm::length(trajectory->target_vel) / 0.1f, 0.0f, 1.0f);
    trajectory->gait_stand[Trajectory::LENGTH/2]  = glm::mix(trajectory->gait_stand[Trajectory::LENGTH/2],  stand_amount, options->extra_gait_smooth);
    trajectory->gait_walk[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_walk[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
    trajectory->gait_jog[Trajectory::LENGTH/2]    = glm::mix(trajectory->gait_jog[Trajectory::LENGTH/2],    0.0f, options->extra_gait_smooth);
    trajectory->gait_crouch[Trajectory::LENGTH/2] = glm::mix(trajectory->gait_crouch[Trajectory::LENGTH/2], 0.0f, options->extra_gait_smooth);
    trajectory->gait_jump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_jump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
    trajectory->gait_bump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_bump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
  } else if (character->crouched_amount > 0.1) {
      //弯腰
    trajectory->gait_stand[Trajectory::LENGTH/2]  = glm::mix(trajectory->gait_stand[Trajectory::LENGTH/2],  0.0f, options->extra_gait_smooth);
    trajectory->gait_walk[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_walk[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
    trajectory->gait_jog[Trajectory::LENGTH/2]    = glm::mix(trajectory->gait_jog[Trajectory::LENGTH/2],    0.0f, options->extra_gait_smooth);
    trajectory->gait_crouch[Trajectory::LENGTH/2] = glm::mix(trajectory->gait_crouch[Trajectory::LENGTH/2], character->crouched_amount, options->extra_gait_smooth);//弯腰
    trajectory->gait_jump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_jump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
    trajectory->gait_bump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_bump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
  } else if ((SDL_JoystickGetAxis(stick, GAMEPAD_TRIGGER_R) / 32768.0) + 1.0) {
      //慢跑
    trajectory->gait_stand[Trajectory::LENGTH/2]  = glm::mix(trajectory->gait_stand[Trajectory::LENGTH/2],  0.0f, options->extra_gait_smooth);
    trajectory->gait_walk[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_walk[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);
    trajectory->gait_jog[Trajectory::LENGTH/2]    = glm::mix(trajectory->gait_jog[Trajectory::LENGTH/2],    1.0f, options->extra_gait_smooth);//慢跑
    trajectory->gait_crouch[Trajectory::LENGTH/2] = glm::mix(trajectory->gait_crouch[Trajectory::LENGTH/2], 0.0f, options->extra_gait_smooth);
    trajectory->gait_jump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_jump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);    
    trajectory->gait_bump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_bump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);    
  } else {
      //走
    trajectory->gait_stand[Trajectory::LENGTH/2]  = glm::mix(trajectory->gait_stand[Trajectory::LENGTH/2],  0.0f, options->extra_gait_smooth);
    trajectory->gait_walk[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_walk[Trajectory::LENGTH/2],   1.0f, options->extra_gait_smooth);//走
    trajectory->gait_jog[Trajectory::LENGTH/2]    = glm::mix(trajectory->gait_jog[Trajectory::LENGTH/2],    0.0f, options->extra_gait_smooth);
    trajectory->gait_crouch[Trajectory::LENGTH/2] = glm::mix(trajectory->gait_crouch[Trajectory::LENGTH/2], 0.0f, options->extra_gait_smooth);
    trajectory->gait_jump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_jump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);  
    trajectory->gait_bump[Trajectory::LENGTH/2]   = glm::mix(trajectory->gait_bump[Trajectory::LENGTH/2],   0.0f, options->extra_gait_smooth);  
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

根据手柄的控制，不断更新将来的帧的可能的轨迹位置和方向

/* Predict Future Trajectory */
  
  glm::vec3 trajectory_positions_blend[Trajectory::LENGTH];
  trajectory_positions_blend[Trajectory::LENGTH/2] = trajectory->positions[Trajectory::LENGTH/2];

  for (int i = Trajectory::LENGTH/2+1; i < Trajectory::LENGTH; i++) {
    //更新61帧以后帧的方向高度和步态
    float bias_pos = character->responsive ? glm::mix(2.0f, 2.0f, character->strafe_amount) : glm::mix(0.5f, 1.0f, character->strafe_amount);
    float bias_dir = character->responsive ? glm::mix(5.0f, 3.0f, character->strafe_amount) : glm::mix(2.0f, 0.5f, character->strafe_amount);
    
    float scale_pos = (1.0f - powf(1.0f - ((float)(i - Trajectory::LENGTH/2) / (Trajectory::LENGTH/2)), bias_pos));
    float scale_dir = (1.0f - powf(1.0f - ((float)(i - Trajectory::LENGTH/2) / (Trajectory::LENGTH/2)), bias_dir));

    trajectory_positions_blend[i] = trajectory_positions_blend[i-1] + glm::mix(
        trajectory->positions[i] - trajectory->positions[i-1], 
        trajectory->target_vel,
        scale_pos); //根据移动速度更新未来帧的位置
        
    /* Collide with walls */
    //单独处理撞墙的情况
    for (int j = 0; j < areas->num_walls(); j++) {
      glm::vec2 trjpoint = glm::vec2(trajectory_positions_blend[i].x, trajectory_positions_blend[i].z);
      if (glm::length(trjpoint - ((areas->wall_start[j] + areas->wall_stop[j]) / 2.0f)) > 
          glm::length(areas->wall_start[j] - areas->wall_stop[j])) { continue; }
      glm::vec2 segpoint = segment_nearest(areas->wall_start[j], areas->wall_stop[j], trjpoint);
      float segdist = glm::length(segpoint - trjpoint);
      if (segdist < areas->wall_width[j] + 100.0) {
        glm::vec2 prjpoint0 = (areas->wall_width[j] +   0.0f) * glm::normalize(trjpoint - segpoint) + segpoint; 
        glm::vec2 prjpoint1 = (areas->wall_width[j] + 100.0f) * glm::normalize(trjpoint - segpoint) + segpoint; 
        glm::vec2 prjpoint = glm::mix(prjpoint0, prjpoint1, glm::clamp((segdist - areas->wall_width[j]) / 100.0f, 0.0f, 1.0f));
        trajectory_positions_blend[i].x = prjpoint.x;
        trajectory_positions_blend[i].z = prjpoint.y;
      }
    }
	//人体方向：当前方向向目标方向慢慢过渡
    trajectory->directions[i] = mix_directions(trajectory->directions[i], trajectory->target_dir, scale_dir);
    //轨迹地形高度，将来的地形高度都是当前时刻中间帧(第60帧)的轨迹高度
    trajectory->heights[i] = trajectory->heights[Trajectory::LENGTH/2]; 
    //步态
    trajectory->gait_stand[i]  = trajectory->gait_stand[Trajectory::LENGTH/2]; 
    trajectory->gait_walk[i]   = trajectory->gait_walk[Trajectory::LENGTH/2];  
    trajectory->gait_jog[i]    = trajectory->gait_jog[Trajectory::LENGTH/2];   
    trajectory->gait_crouch[i] = trajectory->gait_crouch[Trajectory::LENGTH/2];
    trajectory->gait_jump[i]   = trajectory->gait_jump[Trajectory::LENGTH/2];  
    trajectory->gait_bump[i]   = trajectory->gait_bump[Trajectory::LENGTH/2];  
  }
  for (int i = Trajectory::LENGTH/2+1; i < Trajectory::LENGTH; i++) {
    trajectory->positions[i] = trajectory_positions_blend[i];
  }
  
  /* Jumps */
  //单独处理跳跃的情况
  for (int i = Trajectory::LENGTH/2; i < Trajectory::LENGTH; i++) {
    trajectory->gait_jump[i] = 0.0;
    for (int j = 0; j < areas->num_jumps(); j++) {
      float dist = glm::length(trajectory->positions[i] - areas->jump_pos[j]);
      trajectory->gait_jump[i] = std::max(trajectory->gait_jump[i], 
        1.0f-glm::clamp((dist - areas->jump_size[j]) / areas->jump_falloff[j], 0.0f, 1.0f));
    }
  }
  
  /* Crouch Area */
  //单独处理弯腰的情况
  for (int i = Trajectory::LENGTH/2; i < Trajectory::LENGTH; i++) {
    for (int j = 0; j < areas->num_crouches(); j++) {
      float dist_x = abs(trajectory->positions[i].x - areas->crouch_pos[j].x);
      float dist_z = abs(trajectory->positions[i].z - areas->crouch_pos[j].z);
      float height = (sinf(trajectory->positions[i].x/Areas::CROUCH_WAVE)+1.0)/2.0;
      trajectory->gait_crouch[i] = glm::mix(1.0f-height, trajectory->gait_crouch[i], 
          glm::clamp(
            ((dist_x - (areas->crouch_size[j].x/2)) + 
             (dist_z - (areas->crouch_size[j].y/2))) / 100.0f, 0.0f, 1.0f));
    }
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

根据地形，计算当前位置的高度，是将来地形高度的均值

  /* Trajectory Heights */
  for (int i = Trajectory::LENGTH/2; i < Trajectory::LENGTH; i++) {
    trajectory->positions[i].y = heightmap->sample(glm::vec2(trajectory->positions[i].x, trajectory->positions[i].z)); //地形图的当前位置高度
  }
    
  trajectory->heights[Trajectory::LENGTH/2] = 0.0;
  for (int i = 0; i < Trajectory::LENGTH; i+=10) {
    trajectory->heights[Trajectory::LENGTH/2] += (trajectory->positions[i].y / ((Trajectory::LENGTH)/10));//地形高度的平均
  }
          
  glm::vec3 root_position = glm::vec3(
    trajectory->positions[Trajectory::LENGTH/2].x, 
    trajectory->heights[Trajectory::LENGTH/2],
    trajectory->positions[Trajectory::LENGTH/2].z);//人体当前帧的位置和高度
1
2
3
4
5
6
7
8
9
10
11
12
13
14

还有当前人体根关节的朝向

/* Trajectory Rotation */
  for (int i = 0; i < Trajectory::LENGTH; i++) {
    trajectory->rotations[i] = glm::mat3(glm::rotate(atan2f(
      trajectory->directions[i].x,
      trajectory->directions[i].z), glm::vec3(0,1,0)));
  }
  glm::mat3 root_rotation = trajectory->rotations[Trajectory::LENGTH/2];
1
2
3
4
5
6
7

接下来就是计算网络的输入了：

先更新

1-12:所有帧根关节的x坐标
13-24:所有帧根关节的z坐标
25-36:所有帧根关节的x方向
37-48:所有帧根关节的z方向
49-120:所有帧6种步态参数12*6
1
2
3
4
5

  /* Input Trajectory Positions / Directions */
  for (int i = 0; i < Trajectory::LENGTH; i+=10) {
    int w = (Trajectory::LENGTH)/10;
    glm::vec3 pos = glm::inverse(root_rotation) * (trajectory->positions[i] - root_position);//计算所有帧的位置，是基于当前根关节的旋转方向，计算其余帧的位置
    glm::vec3 dir = glm::inverse(root_rotation) * trajectory->directions[i];  //当前根关节的方向乘以轨迹的方向就是人体方向，也就是偏离轨迹多少方向
    pfnn->Xp((w*0)+i/10) = pos.x; pfnn->Xp((w*1)+i/10) = pos.z;//所有帧的xz坐标
    pfnn->Xp((w*2)+i/10) = dir.x; pfnn->Xp((w*3)+i/10) = dir.z;//所有帧的xz朝向
  }
    
  /* Input Trajectory Gaits */
  //所有帧的6种步态信息
  for (int i = 0; i < Trajectory::LENGTH; i+=10) {
    int w = (Trajectory::LENGTH)/10;
    pfnn->Xp((w*4)+i/10) = trajectory->gait_stand[i];
    pfnn->Xp((w*5)+i/10) = trajectory->gait_walk[i];
    pfnn->Xp((w*6)+i/10) = trajectory->gait_jog[i];
    pfnn->Xp((w*7)+i/10) = trajectory->gait_crouch[i];
    pfnn->Xp((w*8)+i/10) = trajectory->gait_jump[i];
    pfnn->Xp((w*9)+i/10) = 0.0; // Unused.
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

再更新

121-213:当前关节的局部位置，注意高度已经减去了地形均值 31*3=93
214-306:当前关节的局部速度31*3
1
2

  /* Input Joint Previous Positions / Velocities / Rotations */
  glm::vec3 prev_root_position = glm::vec3(
    trajectory->positions[Trajectory::LENGTH/2-1].x, 
    trajectory->heights[Trajectory::LENGTH/2-1],
    trajectory->positions[Trajectory::LENGTH/2-1].z);
   
  glm::mat3 prev_root_rotation = trajectory->rotations[Trajectory::LENGTH/2-1];
  
  for (int i = 0; i < Character::JOINT_NUM; i++) {
    int o = (((Trajectory::LENGTH)/10)*10);  
    glm::vec3 pos = glm::inverse(prev_root_rotation) * (character->joint_positions[i] - prev_root_position);
    glm::vec3 prv = glm::inverse(prev_root_rotation) *  character->joint_velocities[i];
    pfnn->Xp(o+(Character::JOINT_NUM*3*0)+i*3+0) = pos.x;
    pfnn->Xp(o+(Character::JOINT_NUM*3*0)+i*3+1) = pos.y;
    pfnn->Xp(o+(Character::JOINT_NUM*3*0)+i*3+2) = pos.z;
    pfnn->Xp(o+(Character::JOINT_NUM*3*1)+i*3+0) = prv.x;
    pfnn->Xp(o+(Character::JOINT_NUM*3*1)+i*3+1) = prv.y;
    pfnn->Xp(o+(Character::JOINT_NUM*3*1)+i*3+2) = prv.z;
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

最后更新高度：

301-342:当前关节附近12帧(已下采样10间隔)的左中右地形高度 12*3=36
1

  /* Input Trajectory Heights */
  for (int i = 0; i < Trajectory::LENGTH; i += 10) {
    int o = (((Trajectory::LENGTH)/10)*10)+Character::JOINT_NUM*3*2;
    int w = (Trajectory::LENGTH)/10;
    glm::vec3 position_r = trajectory->positions[i] + (trajectory->rotations[i] * glm::vec3( trajectory->width, 0, 0));
    glm::vec3 position_l = trajectory->positions[i] + (trajectory->rotations[i] * glm::vec3(-trajectory->width, 0, 0));
    pfnn->Xp(o+(w*0)+(i/10)) = heightmap->sample(glm::vec2(position_r.x, position_r.z)) - root_position.y;
    pfnn->Xp(o+(w*1)+(i/10)) = trajectory->positions[i].y - root_position.y;
    pfnn->Xp(o+(w*2)+(i/10)) = heightmap->sample(glm::vec2(position_l.x, position_l.z)) - root_position.y;
  }
1
2
3
4
5
6
7
8
9
10

接下来直接依据这些输入进行网络的前向计算：

pfnn->predict(character->phase);
1

后续我们实际应用的时候，只需要获得预测结果中的每个关节的局部或者全局旋转矩阵即可，也就是

219-311：当前帧31个关节局部旋转信息，是全局旋转矩阵
1

  for (int i = 0; i < Character::JOINT_NUM; i++) {
    int opos = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*0);
    int ovel = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*1);
    int orot = 8+(((Trajectory::LENGTH/2)/10)*4)+(Character::JOINT_NUM*3*2);
    
    glm::vec3 pos = (root_rotation * glm::vec3(pfnn->Yp(opos+i*3+0), pfnn->Yp(opos+i*3+1), pfnn->Yp(opos+i*3+2))) + root_position;
    glm::vec3 vel = (root_rotation * glm::vec3(pfnn->Yp(ovel+i*3+0), pfnn->Yp(ovel+i*3+1), pfnn->Yp(ovel+i*3+2)));
    glm::mat3 rot = (root_rotation * glm::toMat3(quat_exp(glm::vec3(pfnn->Yp(orot+i*3+0), pfnn->Yp(orot+i*3+1), pfnn->Yp(orot+i*3+2)))));
    
    /*
    ** Blending Between the predicted positions and
    ** the previous positions plus the velocities 
    ** smooths out the motion a bit in the case 
    ** where the two disagree with each other.
    */
    
    character->joint_positions[i]  = glm::mix(character->joint_positions[i] + vel, pos, options->extra_joint_smooth);
    character->joint_velocities[i] = vel;
    character->joint_rotations[i]  = rot;
    
    character->joint_global_anim_xform[i] = glm::transpose(glm::mat4(
      rot[0][0], rot[1][0], rot[2][0], pos[0],
      rot[0][1], rot[1][1], rot[2][1], pos[1],
      rot[0][2], rot[1][2], rot[2][2], pos[2],
              0,         0,         0,      1));//获取全局旋转矩阵
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

得到这个全局旋转矩阵，我们就可以把结果数据重定向到其它各种虚拟角色的骨骼中了，后面所有的代码不再赘述

场景中角色的移动主要包含运动轨迹, 人体朝向, 运动风格切换, 处理流程大概如下:

• 轨迹变化: 其决定因素有左摇杆控制的移动位置, 右摇杆控制的相机位置。主要原因在于人体位置和朝向与相机方位是互为参考系的

• 移动速度: 决定性因素是当前轨迹的方向和指定移动速度,比如沿着西南方以2m/s的速度移动

• 人体朝向: 其决定性因素只有左肩按钮的切换, 面向轨迹方向还是相机方向

• 步态信息: 六种步态风格切换:stand,walk,jog,crouch,jump,bump

• 中间帧(第61帧)的轨迹位置为当前120帧窗口第61帧的位置, 对中间帧之后(62~120)的每个运动都计算轨迹位置

  • 正常情况下,利用公式(9)
    $$TrajectoryBlend(a_0,a_1,t,\tau )=(1-t^{\tau })a_0+t^{\tau }{a}_1$$
    其中$t=\frac{t_{current}-60}{60}$, $t_{current}$代表当前帧索引$(>60)$,实验中$\tau =2.0$, 其实这个就相当于计算某个线段的中间某个位置的值,进而得到混合轨迹位置

  • 如果与墙面碰撞, 对当前轨迹的坐标进行处理, 这样就可以重置第62帧到120帧的轨迹坐标和高度了,

  • 将这部分所有帧的步态信息和高度都初始化为第61帧的对应信息, 但是对于轨迹方向, 是当前轨迹方向与人体朝向的一个插值操作, 同样是公式(9),但是 $\tau =interp(5,3,控制人体朝向手柄数值)$

  • 上述操作全部完成后, 将混合轨迹位置赋值给当前62~120帧的轨迹位置

• 对中间帧及其之后的所有帧, 即第61~120帧的数据做步态处理,更新跳或者弯腰时候步态信息

• 对整个帧段, 即第1~120帧做信息处理

  • 更新撞墙时候的步态信息bump
  • 利用轨迹方向,计算所有帧的轨迹旋转信息, 绕y轴旋转信息
  • 第61~120帧的轨迹高度是对应坐标的地形高度-帧段高度均值
  • 将第$1:10:120$共12帧的轨迹高度的均值,以及第61帧的轨迹(x,z)坐标合起来,作为第61帧的根关节位置root_position, 其旋转量root_rotation就是第61帧的轨迹高度

准备模型输入:

• 1~24维: 总共12帧的xz坐标变化量, 计算方法root_rotaion*(每帧的轨迹位置及高度-第61帧的root_position)
• 25~48维: 总共12帧的xz方向,计算方法root_rotation*轨迹方向
• 49~120维:12帧的6种步态信息
• 121~213维: 第60帧每个关节相对于当前帧的根关节位置变化量
• 214~306维:第60帧相对于当前帧的关节移动速度
• 307~342维: 12帧轨迹的左中右(25cm处)的地形高度变化量, 地形高度-root_position

随后在模型中进行一次前向计算得到对应的输出,针对输出可以通过一系列计算得到预测帧的位置.

与切换场景时候重置整个运动的流程类似:

• 刚重置场景的时候是利用已经记录的均值文件初始人体位置, 但是现在预测出了下一帧的信息, 我们就可以直接使用预测结果得到下一帧关于当前帧产生的位移量,位移速度, 旋转矩阵等相关信息, 在全局空间中做前向运动学操作即可得到全局三维坐标

下一帧更新/参数重置

就是pfnn.cpp第1931行的post_render()函数，当我们预测完下一帧的数据以后，需要将预测完的下一帧当做历史帧，继续预测将来帧。

void post_render() {
            
  /* Update Past Trajectory */
  //之前的帧窗口后移一帧
  for (int i = 0; i < Trajectory::LENGTH/2; i++) {
    trajectory->positions[i]  = trajectory->positions[i+1];
    trajectory->directions[i] = trajectory->directions[i+1];
    trajectory->rotations[i] = trajectory->rotations[i+1];
    trajectory->heights[i] = trajectory->heights[i+1];
    trajectory->gait_stand[i] = trajectory->gait_stand[i+1];
    trajectory->gait_walk[i] = trajectory->gait_walk[i+1];
    trajectory->gait_jog[i] = trajectory->gait_jog[i+1];
    trajectory->gait_crouch[i] = trajectory->gait_crouch[i+1];
    trajectory->gait_jump[i] = trajectory->gait_jump[i+1];
    trajectory->gait_bump[i] = trajectory->gait_bump[i+1];
  }
  
  /* Update Current Trajectory */
  // 更新当前中间帧的轨迹
  float stand_amount = powf(1.0f-trajectory->gait_stand[Trajectory::LENGTH/2], 0.25f);
  
  glm::vec3 trajectory_update = (trajectory->rotations[Trajectory::LENGTH/2] * glm::vec3(pfnn->Yp(0), 0, pfnn->Yp(1)));
  trajectory->positions[Trajectory::LENGTH/2]  = trajectory->positions[Trajectory::LENGTH/2] + stand_amount * trajectory_update;
  trajectory->directions[Trajectory::LENGTH/2] = glm::mat3(glm::rotate(stand_amount * -pfnn->Yp(2), glm::vec3(0,1,0))) * trajectory->directions[Trajectory::LENGTH/2];
  trajectory->rotations[Trajectory::LENGTH/2] = glm::mat3(glm::rotate(atan2f(
      trajectory->directions[Trajectory::LENGTH/2].x,
      trajectory->directions[Trajectory::LENGTH/2].z), glm::vec3(0,1,0)));
      
  /* Collide with walls */
      
  for (int j = 0; j < areas->num_walls(); j++) {
    glm::vec2 trjpoint = glm::vec2(trajectory->positions[Trajectory::LENGTH/2].x, trajectory->positions[Trajectory::LENGTH/2].z);
    glm::vec2 segpoint = segment_nearest(areas->wall_start[j], areas->wall_stop[j], trjpoint);
    float segdist = glm::length(segpoint - trjpoint);
    if (segdist < areas->wall_width[j] + 100.0) {
      glm::vec2 prjpoint0 = (areas->wall_width[j] +   0.0f) * glm::normalize(trjpoint - segpoint) + segpoint; 
      glm::vec2 prjpoint1 = (areas->wall_width[j] + 100.0f) * glm::normalize(trjpoint - segpoint) + segpoint; 
      glm::vec2 prjpoint = glm::mix(prjpoint0, prjpoint1, glm::clamp((segdist - areas->wall_width[j]) / 100.0f, 0.0f, 1.0f));
      trajectory->positions[Trajectory::LENGTH/2].x = prjpoint.x;
      trajectory->positions[Trajectory::LENGTH/2].z = prjpoint.y;
    }
  }

  /* Update Future Trajectory */
  //依据未来的轨迹预测，更新未来帧的轨迹
  for (int i = Trajectory::LENGTH/2+1; i < Trajectory::LENGTH; i++) {
    int w = (Trajectory::LENGTH/2)/10;
    float m = fmod(((float)i - (Trajectory::LENGTH/2)) / 10.0, 1.0);
    trajectory->positions[i].x  = (1-m) * pfnn->Yp(8+(w*0)+(i/10)-w) + m * pfnn->Yp(8+(w*0)+(i/10)-w+1);
    trajectory->positions[i].z  = (1-m) * pfnn->Yp(8+(w*1)+(i/10)-w) + m * pfnn->Yp(8+(w*1)+(i/10)-w+1);
    trajectory->directions[i].x = (1-m) * pfnn->Yp(8+(w*2)+(i/10)-w) + m * pfnn->Yp(8+(w*2)+(i/10)-w+1);
    trajectory->directions[i].z = (1-m) * pfnn->Yp(8+(w*3)+(i/10)-w) + m * pfnn->Yp(8+(w*3)+(i/10)-w+1);
    trajectory->positions[i]    = (trajectory->rotations[Trajectory::LENGTH/2] * trajectory->positions[i]) + trajectory->positions[Trajectory::LENGTH/2];
    trajectory->directions[i]   = glm::normalize((trajectory->rotations[Trajectory::LENGTH/2] * trajectory->directions[i]));
    trajectory->rotations[i]    = glm::mat3(glm::rotate(atan2f(trajectory->directions[i].x, trajectory->directions[i].z), glm::vec3(0,1,0)));
  }
  
  /* Update Phase */
  //平滑之前的相位信息和预测的相位信息
  character->phase = fmod(character->phase + (stand_amount * 0.9f + 0.1f) * 2*M_PI * pfnn->Yp(3), 2*M_PI);
  
  /* Update Camera */
  
  camera->target = glm::mix(camera->target, glm::vec3(
    trajectory->positions[Trajectory::LENGTH/2].x, 
    trajectory->heights[Trajectory::LENGTH/2] + 100, 
    trajectory->positions[Trajectory::LENGTH/2].z), 0.1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

当预测出下一帧动作之后必须对窗口进行滑动, 必须更新新的帧窗口的1~60帧数据信息、第61帧数据信息、第62~120帧的轨迹相关信息:

• 新的1~60帧数据是原始的120帧窗口的第2~61帧数据, 注意原始数据的1~60帧数据不变, 第61帧数据就是用来预测下一帧所使用的帧, 第62~120帧数据的位置已经经过原始位置与gamepad控制参数进行合成了,得到的是新的位置
• 新的第60帧的轨迹位置、朝向和旋转是基于原始第61帧和预测结果的做改变得到的, 因为如果不变的话,此时帧窗口的第60和61帧就不变, 整个人体不会向前移动
• 处理与墙相撞的情况下第61帧$xz$坐标
• 更新第62~120帧的轨迹位置,方向和旋转

重置相位值: $没更新之前的相位值+预测的相位值\ast 2\pi \ast (站立的程度\ast 0.9+0.1)$与$2\pi$取余

更新相机位置: 之前的相机位置与当前的轨迹$xz$位置高度混合插值

逆运动学IK

这一块暂时不做分析，如果玩骨骼动画基本都知道这个用来干啥的，这里是用来消除脚嵌入到地面里面的情况，如果用到unity里面，直接用unity的ik就可以，不过自己写个简单的IK也不难

/* IK */

struct IK {
  
  enum { HL = 0, HR = 1, TL = 2, TR = 3 };
  
  float lock[4];
  glm::vec3 position[4]; 
  float height[4];
  float fade;
  float threshold;
  float smoothness;
  float heel_height;
  float toe_height;
  
  IK()
    : fade(0.075)
    , threshold(0.8)
    , smoothness(0.5)
    , heel_height(5.0)
    , toe_height(4.0) {
    memset(lock, 4, sizeof(float));
    memset(position, 4, sizeof(glm::vec3));
    memset(height, 4, sizeof(float));
  }
  
  void two_joint(
    glm::vec3 a, glm::vec3 b, 
    glm::vec3 c, glm::vec3 t, float eps, 
    glm::mat4& a_pR, glm::mat4& b_pR,
    glm::mat4& a_gR, glm::mat4& b_gR,
    glm::mat4& a_lR, glm::mat4& b_lR) {
    
    float lc = glm::length(b - a);
    float la = glm::length(b - c);
    float lt = glm::clamp(glm::length(t - a), eps, lc + la - eps);
    
    if (glm::length(c - t) < eps) { return; }

    float ac_ab_0 = acosf(glm::clamp(glm::dot(glm::normalize(c - a), glm::normalize(b - a)), -1.0f, 1.0f));
    float ba_bc_0 = acosf(glm::clamp(glm::dot(glm::normalize(a - b), glm::normalize(c - b)), -1.0f, 1.0f));
    float ac_at_0 = acosf(glm::clamp(glm::dot(glm::normalize(c - a), glm::normalize(t - a)), -1.0f, 1.0f));
    
    float ac_ab_1 = acosf(glm::clamp((la*la - lc*lc - lt*lt) / (-2*lc*lt), -1.0f, 1.0f));
    float ba_bc_1 = acosf(glm::clamp((lt*lt - lc*lc - la*la) / (-2*lc*la), -1.0f, 1.0f));
    
    glm::vec3 a0 = glm::normalize(glm::cross(b - a, c - a));
    glm::vec3 a1 = glm::normalize(glm::cross(t - a, c - a));
    
    glm::mat3 r0 = glm::mat3(glm::rotate(ac_ab_1 - ac_ab_0, -a0));
    glm::mat3 r1 = glm::mat3(glm::rotate(ba_bc_1 - ba_bc_0, -a0));
    glm::mat3 r2 = glm::mat3(glm::rotate(ac_at_0,           -a1));
    
    glm::mat3 a_lRR = glm::inverse(glm::mat3(a_pR)) * (r2 * r0 * glm::mat3(a_gR)); 
    glm::mat3 b_lRR = glm::inverse(glm::mat3(b_pR)) * (r1 * glm::mat3(b_gR)); 
    
    for (int x = 0; x < 3; x++)
    for (int y = 0; y < 3; y++) {
      a_lR[x][y] = a_lRR[x][y];
      b_lR[x][y] = b_lRR[x][y];
    }
    
  }
  
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

篇幅受限，且IK与深度学习无关，暂时不做进一步分析，其实这个理论很简单，后续再开一篇博客对这个讲解一下吧，其实就是把末端位置矫正到一个新的位置，返回的是关节新的旋转矩阵。

后续

如果是研究骨骼动画的话，这篇论文的研究价值相当大，非常值得去认真调试每一个参数，尤其是涉及到空间几何的那部分内容，不细心推导，很容易懵圈。研究透彻以后，就可以将这篇论文的代码迁移到各个角色模型上了，我在第一家公司实习的时候，用Ogre游戏引擎折腾了到了公司的虚拟角色骨骼上，第二家公司实习的时候，用unity又用到了另一个虚拟角色的骨骼上。当然由于版权原因没用上，但是受益良多。