数据结构与算法：链表及其应用_当没有连续内存空间,创建一个数组可以装下吗

基本介绍

相比数组，链表是一种稍微复杂一点的数据结构。数组和链表都属于线性表，一个是顺序存储结构，一个是链式存储结构，最主要的的差别是底层存储结构。

数组需要一块连续的内存空间来存储，对内存要求较高，如果申请一个100MB大小的数组，当内存中没有连续的、足够大的存储空间时，即使内存剩余空间总和大于100MB，仍然申请失败。

链表恰恰相反，它并不需要一块连续的内存空间，它通过“指针”将一组零散的内存块串联起来使用，所以如果申请的是 100MB 大小的链表，只要剩余内存不小于于100MB根本不会有问题。如果剩余内存地址是连续的，也是可以的。

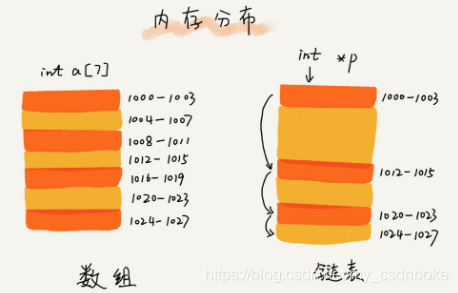
常见的链表结构有单链表、双链表、循环链表。本文主要介绍双链表，以及的它的使用和自定义手写双链表。

单链表

链表通过指针将一组零散的内存块串联在一起。其中，我们把内存块称为链表的**“结点”。为了将所有的结点串起来，每个链表的结点除了存储数据之外，还需要记录链上的下一个结点的地址。如图所示，我们把这个记录下个结点地址的指针叫作后继指针** next。

其中有两个结点是比较特殊的，它们分别是第一个结点和最后一个结点。我们习惯性地把第一个结点叫作头结点，把最后一个结点叫作尾结点。其中，头结点用来记录链表的基地址。有了它，我们就可以遍历得到整条链表。而尾结点特殊的地方是：指针不是指向下一个结点，而是指向一个空地址 NULL，表示这是链表上最后一个结点。

与数组一样，链表也支持数据的查找、插入和删除操作。在进行数组的插入、删除操作时，为了保持内存数据的连续性，需要做大量的数据搬移，所以时间复杂度是 O(n)。而在链表中插入或者删除一个数据，我们并不需要为了保持内存的连续性而搬移结点，因为链表的存储空间本身就不是连续的。所以，在链表中插入和删除一个数据是非常快速的。

从图中我们可以看出，针对链表的插入和删除操作，我们只需要考虑相邻结点的指针改变，所以对应的时间复杂度是 O(1)。

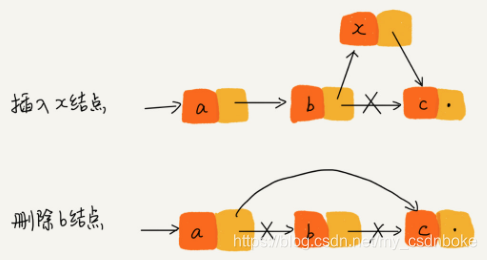
但是，有利就有弊。链表要想随机访问第 k 个元素，就没有数组那么高效了。因为链表中的数据并非连续存储的，所以无法像数组那样，根据首地址和下标，通过寻址公式就能直接计算出对应的内存地址，而是需要根据指针一个结点一个结点地依次遍历，直到找到相应的结点。

可以把链表想象成一个队伍，队伍中的每个人都只知道自己后面的人是谁，所以当我们希望知道排在第 k 位的人是谁的时候，我们就需要从第一个人开始，一个一个地往下数。所以，链表随机访问的性能没有数组好，需要 O(n) 的时间复杂度。

双链表

单向链表只有一个方向，结点只有一个后继指针 next 指向后面的结点。而双向链表，顾名思义，它支持两个方向，每个结点不止有一个后继指针 next 指向后面的结点，还有一个前驱指针 prev 指向前面的结点。

双向链表需要额外的两个空间来存储后继结点和前驱结点的地址。所以，如果存储同样多的数据，双向链表要比单链表占用更多的内存空间。虽然两个指针比较浪费存储空间，但可以支持双向遍历，这样也带来了双向链表操作的灵活性。那相比单链表，双向链表适合解决哪种问题呢？

从结构上来看，双向链表可以支持 O(1) 时间复杂度的情况下找到前驱结点，正是这样的特点，也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。

单链表的插入、删除操作的时间复杂度已经是 O(1) 了，双向链表还能再怎么高效呢？别着急，刚刚的分析比较偏理论，很多数据结构和算法书籍中都会这么讲，但是这种说法实际上是不准确的，或者说是有先决条件的。再来带你分析一下链表的两个操作。

先来看删除操作

在实际的软件开发中，从链表中删除一个数据无外乎这两种情况：

• 删除结点中“值等于某个给定值”的结点；
• 删除给定指针指向的结点。

对于第一种情况，不管是单链表还是双向链表，为了查找到值等于给定值的结点，都需要从头结点开始一个一个依次遍历对比，直到找到值等于给定值的结点，然后再通过我前面讲的指针操作将其删除。

尽管单纯的删除操作时间复杂度是 O(1)，但遍历查找的时间是主要的耗时点，对应的时间复杂度为 O(n)。根据时间复杂度分析中的加法法则，删除值等于给定值的结点对应的链表操作的总时间复杂度为 O(n)。

对于第二种情况，我们已经找到了要删除的结点，但是删除某个结点 q 需要知道其前驱结点，而单链表并不支持直接获取前驱结点，所以，为了找到前驱结点，我们还是要从头结点开始遍历链表，直到 p->next=q，说明 p 是 q 的前驱结点。

但是对于双向链表来说，这种情况就比较有优势了。因为双向链表中的结点已经保存了前驱结点的指针，不需要像单链表那样遍历。所以，针对第二种情况，单链表删除操作需要 O(n) 的时间复杂度，而双向链表只需要在 O(1) 的时间复杂度内就搞定了！

同理，如果我们希望在链表的某个指定结点前面插入一个结点，双向链表比单链表有很大的优势。双向链表可以在 O(1) 时间复杂度搞定，而单向链表需要 O(n) 的时间复杂度。你可以参照我刚刚讲过的删除操作自己分析一下。

除了插入、删除操作有优势之外，对于一个有序链表，双向链表的按值查询的效率也要比单链表高一些。因为，我们可以记录上次查找的位置 p，每次查询时，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，所以平均只需要查找一半的数据。

• 第一次处理：将所有元素根据点数分别存放到9个链表中，然后将链表连接起来，此时的链表中元素的点数是有序的
• 第二次处理：将所有元素根据花色分别存放到3个链表中，然后将链表连接起来，此时的链表中元素的点数和花色均是有序的

代码如下：

/**
 * 麻将类
 */
public class Mahjong {
   
    public int suit;//筒(1)，万(2)，条(3)
    public int rank;//点数 一  二  三

    public Mahjong(int suit, int rank) {
   
        this.suit = suit;
        this.rank = rank;
    }

    @Override
    public String toString() {
   
        return "("+this.suit+" "+this.rank+")";
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

测试类

/**
 * 链表的应用
 * 链式基数排序
 * 麻将的排序
 */
public class Client {
   

    @Test
    public void test() {
   
        LinkedList<Mahjong> list = new LinkedList<Mahjong>();
        list.add(new Mahjong(3,1));
        list.add(new Mahjong(2,3));
        list.add(new Mahjong(3,7));
        list.add(new Mahjong(1,1));
        list.add(new Mahjong(3,9));
        list.add(new Mahjong(2,2));
        list.add(new Mahjong(3,2));
        list.add(new Mahjong(1,3));
        list.add(new Mahjong(3,8));
        System.out.println(list);
        //[(3 1), (2 3), (3 7), (1 1), (3 9), (2 2), (3 2), (1 3), (3 8)]
        radixSort(list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23