二叉树的前序遍历、中序遍历、后序遍历、层序遍历的时间复杂度和空间复杂度_中序遍历时间复杂度

非递归版：
由于不管是先序遍历还是中序遍历以及后序遍历，我们都需要利用一个辅助栈来进行每个节点的存储打印，所以每个节点都要进栈和出栈，不过是根据那种遍历方式改变的是每个节点的进栈顺序，所以时间复杂度为O(n)，同样空间复杂度也为O(n)，n为结点数。
层序遍历是通过队列来进行每个节点的存储打印的，所以时间复杂度和空间复杂度也与前三种遍历方式一样。
递归版：
空间复杂度与系统堆栈有关，系统栈需要记住每个节点的值，所以空间复杂度为O(n)。时间复杂度应该为O(n)，根据公式T(n)=2T(n/2)+1=2(2T(n/4)+1)+1=2^logn+2^(logn-1)+...+2+1 ~= n，所以时间复杂度为O(n)。

相关代码如下（包括递归版和非递归版）

BiTree.h:

#pragma once
typedef char TElemType;
typedef struct BiTNode 
{
	TElemType data;
	struct BiTNode* Ichild, * rchild;
}BiTNode,*BiTree;
int CreateBiTree(BiTree& T);				//先序构造二叉树
int PreOrderTraverse(BiTree T);				//先序遍历二叉树
int InOrderTraverse(BiTree T);				//中序遍历二叉树
int PostOrderTraverse(BiTree T);			//后序遍历二叉树
int LevelOrderTraverse(BiTree T);			//层序遍历二叉树
int PreOrderTraverse1(BiTree T);			//先序遍历二叉树，非递归版
int InOrderTraverse1(BiTree T);				//中序遍历二叉树，非递归版
int PostOederTraverse1(BiTree T);			//后序遍历二叉树，非递归版
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

BiTree.cpp:

#include "BitTree.h"
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
int CreateBiTree(BiTree& T)
{
	TElemType e;
	cin >> e;
	if (e == '#')//#表示空树
		T = NULL;
	else
	{
		T = (BiTNode*)malloc(sizeof(BiTNode));
		if (!T)
			exit(0);
		else
		{
			T->data = e;//生成根节点
			CreateBiTree(T->Ichild);//构造左子树
			CreateBiTree(T->rchild);//构造右子树
		}
	}
	return 1;
}

int PreOrderTraverse(BiTree T)//前序遍历
{
	if (T) { //判T是否为空树
		cout << T->data; //输出T节点的数据
		if (PreOrderTraverse(T->Ichild)); //递归遍历左子树
		if (PreOrderTraverse(T->rchild)); //递归遍历右子树
		return 0;
	}
	else
		return 1;
}

int InOrderTraverse(BiTree T)//中序遍历
{
	if (T) {//判T是否为空树，递归边界
		if (InOrderTraverse(T->Ichild));//递归遍历左子树
		cout << T->data;//输出T节点的数据
		if (InOrderTraverse(T->rchild));//递归遍历右子树
		return 0;
	}
	else
		return 1;
}

int PostOrderTraverse(BiTree T)//后序遍历
{
	if (T){//判T是否为空树
		if(PostOrderTraverse(T->Ichild));//递归遍历左子树
		if (PostOrderTraverse(T->rchild));//递归遍历右子树
		cout << T->data;//输出T节点的数据
		return 0;
	}
	else 
		return 1;
}

int LevelOrderTraverse(BiTree T)//层序遍历
{
	if (T == NULL)
		return 0;
	queue<BiTree> Q;
	Q.push(T);//把根结点推入
	while (!Q.empty())//循环结束之后再次判断，直到队列为空
	{
		cout << Q.front()->data;
		if (Q.front()->Ichild!= NULL)//左节点进队列
			Q.push(Q.front()->Ichild);
		if (Q.front()->rchild != NULL)//右节点进队列
			Q.push(Q.front()->rchild);
		Q.pop();//队头出列
	}
	cout << endl;
	return 1;
}

int PreOrderTraverse1(BiTree T)//前序遍历
{
/*
对于任一结点P：
	1)访问结点P，并将结点P入栈;
	2)判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1);若不为空，则将P的左孩子置为当前的结点P;
	3)直到P为NULL并且栈为空，则遍历结束。
*/
	stack<BiTree> s;
	BiTree p = T;//根节点
	while (p != NULL || !s.empty())
	{
		while (p != NULL)//根左右
		{
			cout << p->data;
			s.push(p);
			p = p->Ichild;
		}
		if (!s.empty())
		{
			p = s.top();//得到根节点
			s.pop();//根节点出栈
			p = p->rchild;//
		}
	}
	return 0;
}

int InOrderTraverse1(BiTree T)//中序遍历
{
/*
对于任一结点P：
	1)若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
	2)若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
	3)直到P为NULL并且栈为空则遍历结束
*/
	stack<BiTree> s;
	BiTree p = T;
	while (p != NULL || !s.empty())
	{
		while (p != NULL)
		{
			s.push(p);
			p = p->Ichild;
		}
		if (!s.empty())
		{
			p = s.top();//得到最底端的左节点
			cout << p->data;//输出节点值
			s.pop();
			p = p->rchild;
		}
	}
	return 0;
}

int PostOederTraverse1(BiTree T)//后序遍历
{
/*
要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点P，先将其入栈。如果P不存在左孩子和右孩子，则可以直接访问它；
或者P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。
若非上述两种情况，则将P的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，左孩子和右孩子都在根结点前面被访问。
*/
	stack<BiTree> s;
	BiTree cur;//当前结点
	BiTree pre = NULL;//前一次访问的结点
	s.push(T);//根节点出栈
	while (!s.empty())
	{
		cur = s.top();
		if ((cur->Ichild == NULL && cur->rchild == NULL) ||
			(pre != NULL && (pre == cur->Ichild || pre == cur->rchild)))
		{
			cout << cur->data;//当前结点没有孩子节点或孩子节点都已经被访问了
			s.pop();
			pre = cur;
		}
		else
		{
			if (cur->rchild != NULL)
				s.push(cur->rchild);//右孩子先进栈
			if (cur->Ichild != NULL)
				s.push(cur->Ichild);//左孩子后进栈，保证在取栈顶元素时，左孩子在右孩子之前被访问
		}
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168

test.cpp:

#include"BitTree.h"
#include<iostream>
using namespace std;

int main()
{
	cout << "输入二叉树：";
	BiTree T;
	CreateBiTree(T);
	cout << "先序遍历（递归）：\t";
	PreOrderTraverse(T);

	cout << "\n先序遍历（非递归）：\t";
	PreOrderTraverse1(T);

	cout << "\n中序遍历（递归）：\t";
	InOrderTraverse(T);

	cout << "\n中序遍历（非递归）：\t";
	InOrderTraverse1(T);

	cout << "\n后序遍历（递归）：\t";
	PostOrderTraverse(T);

	cout << "\n后序遍历（非递归）：\t";
	PostOederTraverse1(T);

	cout << "\n层序遍历（非递归）：\t";
	LevelOrderTraverse(T);


	//ABC##DE#G##F###
	system("pause");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

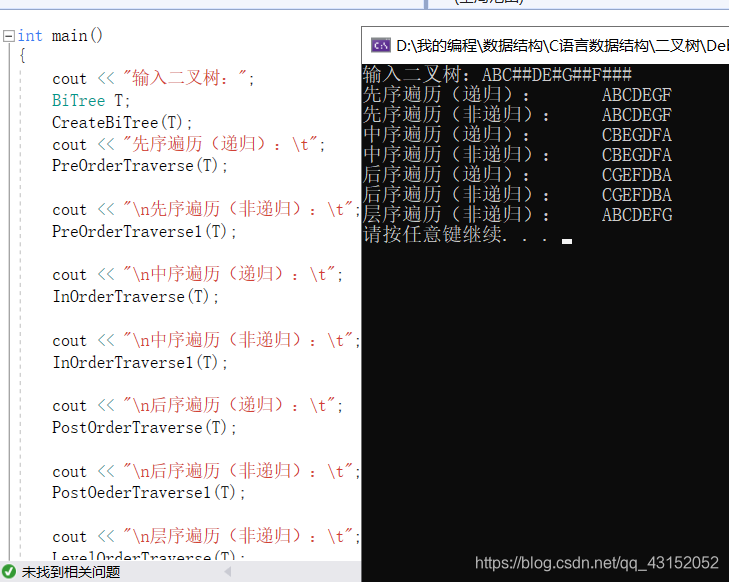
运行结果如下：