- 1凸多边形最优三角形剖分_凸多边形最优三角剖分
- 2Moveit! 学习记录3——moveit与深度学习(yolov8)_ros yolov8
- 3关系型数据库(RDB)和非关系型数据库(nosql)_rdb是什么数据库
- 4python闪光培训班 费用-python社招面试经验分享
- 5最常见的软件测试面试题及答案_软件测试面试常见问题及答案
- 6【小程序教程】微信小程序之request网络请求_微信小程序 request
- 7Hadoop hdfs删除、查看文件_在hdfs根目录下有一个文件a.txt,我们应该如何删除
- 8OpenCV 入门(六) —— Android 下的人脸识别_android集成opencv人脸识别
- 9『FPGA通信接口』串行通信接口-IIC(2)EEPROM读写控制器_at24c04用什么协议来交互
- 10使用mount挂载磁盘mount: wrong fs type, bad option, bad superblock on 以及Centos7.9服务器LVM方式挂载磁盘时的问题_wrong fs type bad option
一文搞懂Transformer中的位置编码Positional Encoding_transformer position encoding
赞
踩
Transformer为什么需要位置编码
在自然语言处理中,元素(如单词、字符)的顺序对于理解句子的含义至关重要。例如,"The dog bites the man."和"The man bites the dog."这两句话虽然包含相同的词汇,但意义完全不同。
没有位置编码的Transformer模型并不能捕捉序列的顺序,交换单词位置后 attention map 的对应位置数值也会进行交换,然而并不会产生数值变化,即没有词序信息。
为了让Transformer能够理解这种顺序信息,需要引入一种机制来编码每个元素在序列中的位置或顺序。
位置编码应具备的特性
对于输入是一整排的tokens:
- 绝对位置信息。a1是第一个token,a2是第二个token…
- 相对位置信息。a2在a1的后面一位,a4在a2的后面两位…
- 不同位置间的距离。a1和a3差两个位置,a1和a4差三个位置…
用整型值标记位置
一种自然而然的想法是,给第一个token标记1,给第二个token标记2…,以此类推。
这种方法产生了以下几个主要问题:
(1)模型可能遇见比训练时所用的序列更长的序列。不利于模型的泛化。
(2)模型的位置表示是无界的。随着序列长度的增加,位置值会越来越大。 这会导致与 token embedding 合并后出现特征在数值的倾斜和干扰
用[0,1]范围标记位置
为了解决整型值带来的问题,可以考虑将位置值的范围限制在[0, 1]之内,其中,0表示第一个token,1表示最后一个token。比如有3个token,那么位置信息就表示成[0, 0.5, 1];若有四个token,位置信息就表示成[0, 0.33, 0.69, 1]。
但这样产生的问题是,当序列长度不同时,token间的相对距离是不一样的。例如在序列长度为3时,token间的相对距离为0.5;在序列长度为4时,token间的相对距离就变为0.33。这会导致长文本的相对位置关系被稀释。
二进制向量标记位置
这下所有的值都是有界的(位于0,1之间),且transformer中的d_model本来就足够大,基本可以把我们要的每一个位置都编码出来了。
但是这种编码方式也存在问题:这样编码出来的位置向量,处在一个离散的空间中,不同位置间的变化是不连续的。假设d_model = 2,我们有4个位置需要编码,这四个位置向量可以表示成[0,0],[0,1],[1,0],[1,1]。我们把它的位置向量空间做出来:
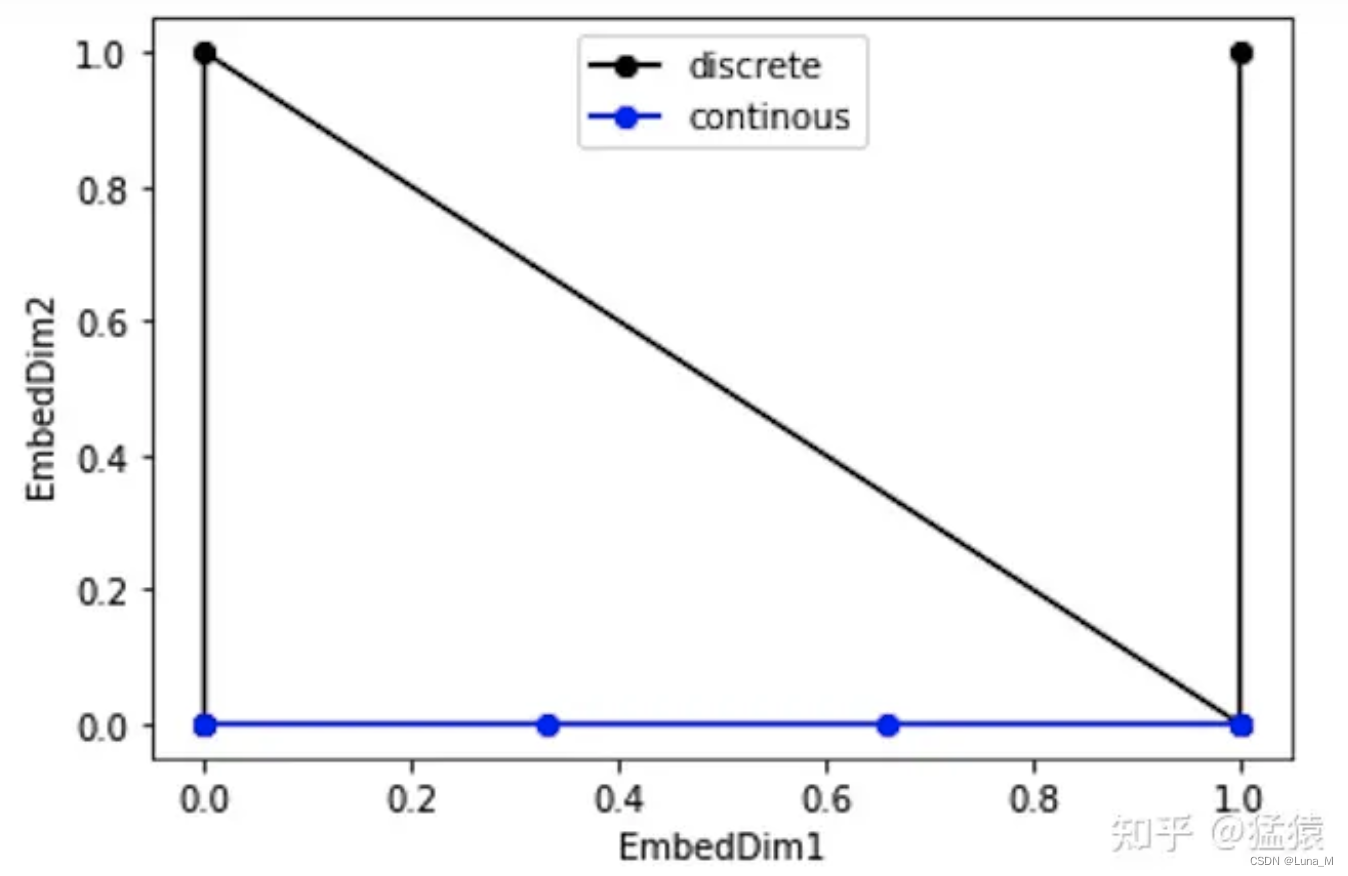
如果我们能把离散空间(黑色的线)转换到连续空间(蓝色的线),那么我们就能解决位置距离不连续的问题。
用周期函数来表示位置
回想一下,现在我们需要一个有界又连续的函数,最简单的,正弦函数sin就可以满足这一点。我们可以考虑把位置向量当中的每一个元素都用一个sin函数来表示,则第t个token的位置向量可以表示为:
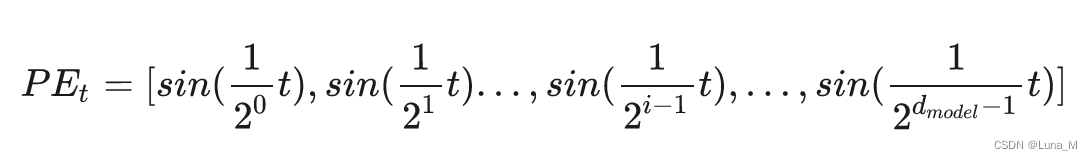 通过频率
1
2
i
−
1
\frac{1}{2^{i-1}}
2i−11 来控制sin函数的波长,频率不断减小,则波长不断变大,此时sin函数对t的变动越不敏感。
通过频率
1
2
i
−
1
\frac{1}{2^{i-1}}
2i−11 来控制sin函数的波长,频率不断减小,则波长不断变大,此时sin函数对t的变动越不敏感。
波长是周期函数(如正弦和余弦函数)重复一个完整模式的最小距离。在数学和物理中,正弦和余弦函数的基本形式是sin(x)和
cos(x),其中x是以弧度为单位的角度,这两个函数的周期是
2π弧度,意味着每增加2π的角度,函数值重复一次。由于正弦和余弦函数的周期性为2π,这意味着当输入变化2π弧度时,函数值完成一个周期,因此在这种情况下,我们说"波长"为2π。
sin( 1 2 i − 1 t \frac{1}{2^{i-1}}t 2i−11t)的波长为 2 i − 1 ⋅ 2^{i-1}\cdot 2i−1⋅ 2π
这也类似于二进制编码,每一位上都是0和1的交互,越往低位走(越往左边走),交互的频率越慢。

目前为止,我们的位置向量实现了如下功能:
(1)每个token的向量唯一(每个sin函数的频率足够小)
(2)位置向量的值是有界的,且位于连续空间中。模型在处理位置向量时更容易泛化,即更好处理长度和训练数据分布不一致的序列(sin函数本身的性质)
那现在我们对位置向量再提出一个要求,不同的位置向量是可以通过线性转换得到的。这样,我们不仅能表示一个token的绝对位置,还可以表示一个token的相对位置,即我们想要:
 这里,T表示一个线性变换矩阵。观察这个目标式子,联想到在向量空间中一种常用的线形变换——旋转。在这里,我们将t想象为一个角度,那么 就是其旋转的角度,则上面的式子可以进一步写成:
这里,T表示一个线性变换矩阵。观察这个目标式子,联想到在向量空间中一种常用的线形变换——旋转。在这里,我们将t想象为一个角度,那么 就是其旋转的角度,则上面的式子可以进一步写成:
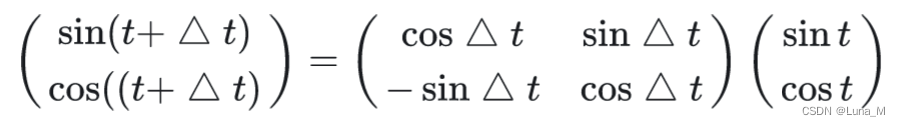
有了这个构想,我们就可以把原来元素全都是sin函数的
P
E
t
PE_t
PEt做一个替换,我们让位置两两一组,分别用sin和cos的函数对来表示它们。
用sin和cos交替来表示位置
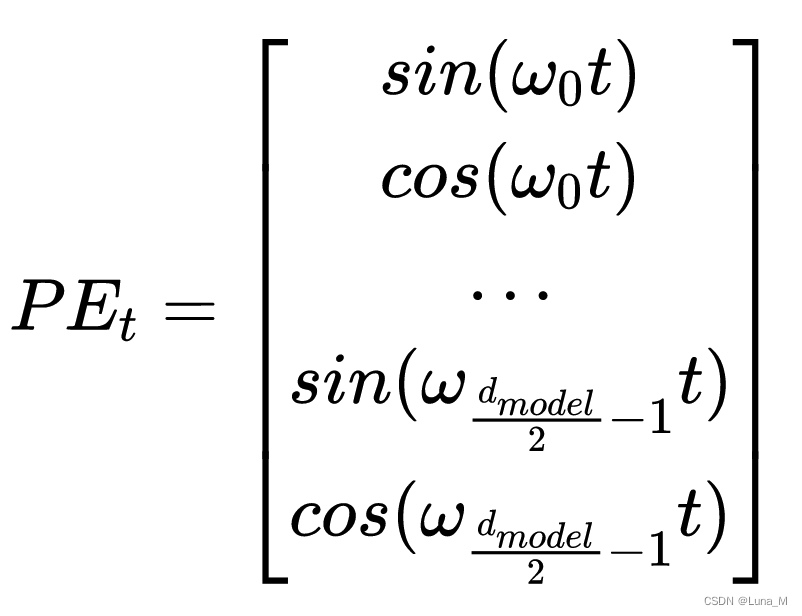

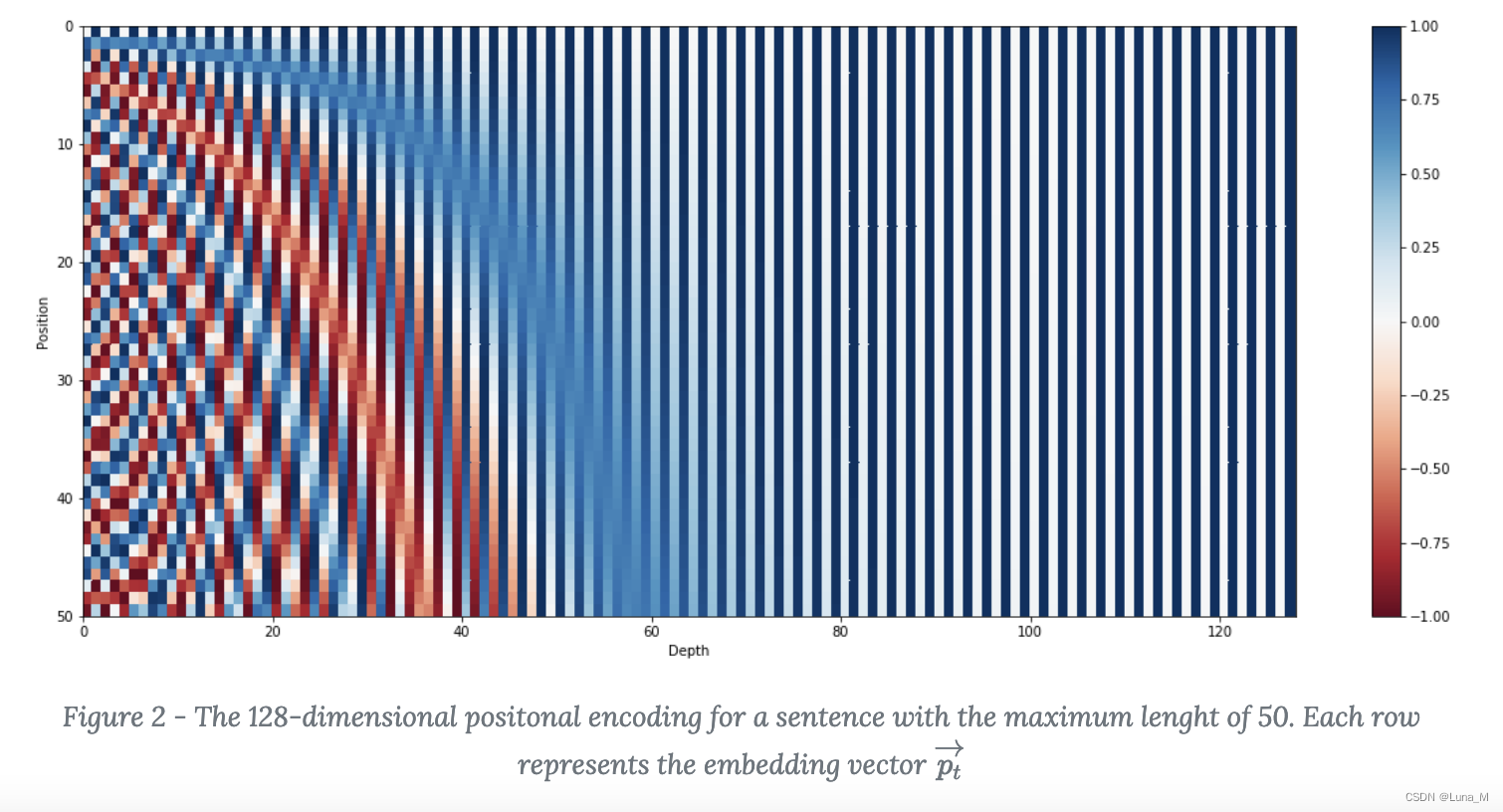 上图是一串序列长度为50,位置编码维度为128的位置编码可视化结果。可以发现,由于sin/cos函数的性质,位置向量的每一个值都位于[-1, 1]之间。同时,纵向来看,图的右半边几乎都是蓝色的,这是因为越往后的位置,频率越小,波长越长,所以不同的t对最终的结果影响不大。而越往左边走,颜色交替的频率越频繁。
上图是一串序列长度为50,位置编码维度为128的位置编码可视化结果。可以发现,由于sin/cos函数的性质,位置向量的每一个值都位于[-1, 1]之间。同时,纵向来看,图的右半边几乎都是蓝色的,这是因为越往后的位置,频率越小,波长越长,所以不同的t对最终的结果影响不大。而越往左边走,颜色交替的频率越频繁。
当我们计算两个位置 p o s 1 pos_1 pos1和 p o s 2 pos_2 pos2之间的位置编码的点积时,实际上我们是在对应维度上将正弦函数与正弦函数、余弦函数与余弦函数相乘,并将结果相加。考虑到正弦和余弦函数的三角恒等式,我们可以将点积简化。
 这说明,两个位置编码的点积只取决于这两个位置之间的差
p
o
s
1
−
p
o
s
2
pos_1-pos_2
pos1−pos2,也就是它们之间的偏移量。因此,点积的结果反映了两个位置之间的相对距离,而与它们的绝对位置无关。
这说明,两个位置编码的点积只取决于这两个位置之间的差
p
o
s
1
−
p
o
s
2
pos_1-pos_2
pos1−pos2,也就是它们之间的偏移量。因此,点积的结果反映了两个位置之间的相对距离,而与它们的绝对位置无关。
这个特性使得Transformer能够通过计算位置编码的点积来捕获序列中元素之间的相对位置关系。
当我们说两个位置编码的点积仅取决于它们之间的距离时,我们是基于这样的事实:点积通过余弦函数反映了两个位置之间角度差的余弦值,而这个角度差直接对应于它们在序列中的相对距离。换句话说,点积反映的是两个位置编码向量在高维空间中的相对方向关系,而这个关系只取决于这两个位置之间的距离。
由于cos函数的对称性。我们可以分别训练不同维度的位置向量,然后以某个位置向量
P
E
t
PE_t
PEt为基准,去计算其左右和它相距 的位置向量的点积,可以得到如下结果:


因此,一种好的位置编码方案需要满足以下几条要求:
- 它能为每个时间步输出一个独一无二的编码
- 它的值应该是有界的,模型应该能毫不费力地泛化到更长的句子
- 不同长度的句子之间,任何两个时间步之间的距离应该保持一致
拓展思考
位置编码为什么不是拼接

位置信息在Transformer模型的上层是否会消失



