1.8 数据结构之 DFS_dfs算法数据结构

编程总结

本篇参考LeetCode学习 https://leetcode-cn.com/leetbook/read/dfs/euapvg/

1. 勇往直前的深度优先遍历

「一条路走到底，不撞南墙不回头」是对「深度优先遍历」的最直观描述。下面的视频演示了以「深度优先遍历」的方式「走迷宫找出口」的搜索轨迹。
说明：

深度优先遍历 只要前面有可以走的路，就会一直向前走，直到无路可走才会回头；
「无路可走」有两种情况：① 遇到了墙；② 遇到了已经走过的路；
在「无路可走」的时候，沿着原路返回，直到回到了还有未走过的路的路口，尝试继续走没有走过的路径；
有一些路径没有走到，这是因为找到了出口，程序就停止了；
「深度优先遍历」也叫「深度优先搜索」，遍历是行为的描述，搜索是目的（用途）；
遍历不是很深奥的事情，把 所有 可能的情况都看一遍，才能说「找到了目标元素」或者「没找到目标元素」。遍历也称为 穷举，穷举的思想在人类看来虽然很不起眼，但借助 计算机强大的计算能力，穷举可以帮助我们解决很多专业领域知识不能解决的问题。

1.1 搜索

「遍历」和「搜索」可以看作是两个的等价概念，通过遍历 所有 的可能的情况达到搜索的目的。遍历是手段，搜索是目的。因此「深度优先遍历」也叫「深度优先搜索」

1.2 树的深度优先遍历

我们以「二叉树」的深度优先遍历为例，向大家介绍树的深度优先遍历。
二叉树的深度优先遍历从「根结点」开始，依次 「递归地」 遍历「左子树」的所有结点和「右子树」的所有结点。

事实上，「根结点 → 右子树 → 左子树」也是一种深度优先遍历的方式，为了符合人们「先左再右」的习惯。如果没有特别说明，我们在这个专题里，树的深度优先遍历默认都按照 「根结点 → 左子树 → 右子树」 的方式进行。

二叉树深度优先遍历的递归终止条件：遍历完一棵树的 所有 叶子结点，等价于遍历到 空结点。大家可以点击下面的幻灯片查看深度优先遍历的结果。

遍历可以用于搜索，思想是穷举，遍历是实现搜索的手段；
树的「前、中、后」序遍历都是深度优先遍历；
树的后序遍历很重要；
由于图中存在环（回路），图的深度优先遍历需要记录已经访问过的结点，以避免重复访问；
遍历是一种简单、朴素但是很重要的算法思想，很多树和图的问题就是在树和图上执行一次遍历，在遍历的过程中记录有用的信息，得到需要结果，区别在于为了解决不同的问题，在遍历的时候传递了不同的 与问题相关 的数据。

二叉树的深度优先遍历从「根结点」开始，依次 「递归地」 遍历「左子树」的所有结点和「右子树」的所有结点

1. 前序遍历

对于任意一棵子树，先输出根结点，再递归输出左子树的 所有 结点、最后递归输出右子树的 所有 结点。上图前序遍历的结果就是深度优先遍历的结果：[0、1、3、4、7、2、5、8、9、6、10]。

2. 中序遍历

对于任意一棵子树，先递归输出左子树的 所有 结点，然后输出根结点，最后递归输出右子树的 所有 结点。上图中序遍历的结果是：
[3、1、7、4、0、8、5、9、2、10、6]。

3. 后序遍历

对于任意一棵子树，总是先递归输出左子树的 所有 结点，然后递归输出右子树的 所有 结点，最后输出根结点。后序遍历体现的思想是：先必需得到左右子树的结果，才能得到当前子树的结果，这一点在解决一些问题的过程中非常有用。上图后序遍历的结果是：
[3、7、4、1、8、9、5、10、6、2、0]。

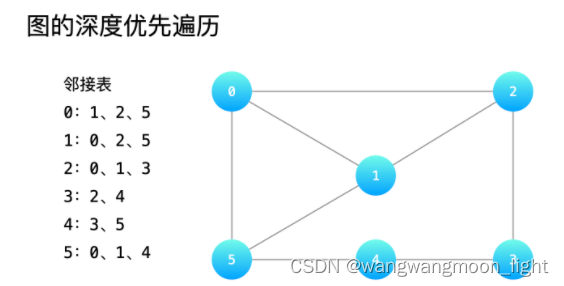
1.3 图的深度优先遍历

深度优先遍历有「回头」的过程，在树中由于不存在「环」（回路），对于每一个结点来说，每一个结点只会被递归处理一次。而**「图」中由于存在「环」（回路）**，就需要 记录已经被递归处理的结点（通常使用布尔数组或者哈希表），以免结点被重复遍历到。

1.4 总结

遍历可以用于搜索，思想是穷举，遍历是实现搜索的手段；
树的「前、中、后」序遍历都是深度优先遍历；
树的后序遍历很重要；
由于图中存在环（回路），图的深度优先遍历需要记录已经访问过的结点，以避免重复访问；
遍历是一种简单、朴素但是很重要的算法思想，很多树和图的问题就是在树和图上执行一次遍历，在遍历的过程中记录有用的信息，得到需要结果，区别在于为了解决不同的问题，在遍历的时候传递了不同的 与问题相关 的数据。

2. 数据结构-栈

2.1 深度优先遍历的两种实现方式

在深度优先遍历的过程中，需要将 当前遍历到的结点 的相邻结点 暂时保存 起来，以便在回退的时候可以继续访问它们。遍历到的结点的顺序呈现「后进先出」的特点，因此 深度优先遍历可以通过「栈」实现。

再者，深度优先遍历有明显的递归结构。我们知道支持递归实现的数据结构也是栈。因此实现深度优先遍历有以下两种方式：

编写递归方法；
编写栈，通过迭代的方式实现。

144. 二叉树的前序遍历

void PreOrder(struct TreeNode *root, int *ret, int *retIndex)
{
	if (root == NULL) {
		return;
	}
	// 根左右 -- 前序
	ret[(*retIndex)++] = root->val;
	PreOrder(root->left, ret, retIndex);
	PreOrder(root->right, ret, retIndex);
}
// 二叉树前序遍历结果存放在 ret 里，idx由retIndex表示
int *preorderTraversal(struct TreeNode *root, int *returnSize)
{
	int retIndex = 0;
	int *ret = (int *)malloc(sizeof(int) * 100);
	memset(ret, 0, sizeof(int) * 100);

	PreOrder(root, ret, &retIndex);
	*returnSize = retIndex;

	return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

迭代

int* preorderTraversal(struct TreeNode *root, int *returnSize) {
    int *res = malloc(sizeof(int) * 2000);
    *returnSize = 0;
    if (root == NULL) {
        return res;
    }

    struct TreeNode *stk[2000];
    struct TreeNode *node = root;
    int top = 0;
    // 根左右 -- 前序
    while (top > 0 || node != NULL) {
        while (node != NULL) {
            res[(*returnSize)++] = node->val; // 边遍历边输出结果
            stk[top++] = node;
            node = node->left;
        }
        node = stk[--top]; // 一一出栈
        node = node->right;
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历

void inorder(struct TreeNode *root, int *res, int *resSize) {
    if (!root) {
        return;
    }
    // 左根右 -- 中序
    inorder(root->left, res, resSize);
    res[(*resSize)++] = root->val;
    inorder(root->right, res, resSize);
}
int *inorderTraversal(struct TreeNode *root, int *returnSize) {
    int* res = malloc(sizeof(int) * 501);
    *returnSize = 0;
    inorder(root, res, returnSize);
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

迭代实现

int *inorderTraversal(struct TreeNode *root, int *returnSize) {
    *returnSize = 0;
    int* res = malloc(sizeof(int) * 501);
    struct TreeNode **stk = malloc(sizeof(struct TreeNode*) * 501);
    int top = 0;
    // 左根右 -- 中序
    while (root != NULL || top > 0) {
        while (root != NULL) { // 与前序遍历区别：先不会记录结果，先递下来到叶子节点
            stk[top++] = root;
            root = root->left;
        }
        root = stk[--top];
        res[(*returnSize)++] = root->val; 
        root = root->right;
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

145. 二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历

void postorder(struct TreeNode *root, int *res, int *resSize) {
    if (root == NULL) {
        return;
    }
    // 左右根 -- 后序
    postorder(root->left, res, resSize);
    postorder(root->right, res, resSize);
    res[(*resSize)++] = root->val;
}
int *postorderTraversal(struct TreeNode *root, int *returnSize) {
    int *res = malloc(sizeof(int) * 2001);
    *returnSize = 0;
    postorder(root, res, returnSize);
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

迭代实现

int *postorderTraversal(struct TreeNode *root, int *returnSize) {
    int *res = malloc(sizeof(int) * 2001);
    *returnSize = 0;
    if (root == NULL) {
        return res;
    }
    struct TreeNode **stk = malloc(sizeof(struct TreeNode *) * 2001);
    int top = 0;
    struct TreeNode *prev = NULL;
    while (root != NULL || top > 0) {
        while (root != NULL) {
            stk[top++] = root;
            root = root->left;
        }
        root = stk[--top];
        if (root->right == NULL || root->right == prev) {
            res[(*returnSize)++] = root->val;
            prev = root;
            root = NULL;
        } else {
            stk[top++] = root;
            root = root->right;
        }
    }
    return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

总结

深度优先遍历通过「栈」实现；
深度优先遍历符合「后进先出」规律，可以借助「栈」实现；
深度优先遍历有明显的「递归」结构，递归也是借助「栈」实现的；
因此深度优先遍历一般通过「递归」实现，底层借助了「栈」这个数据结构作为支持；
栈虽然结构（数组或者链表）和规则定义简单（后进先出），但是它在算法的世界里发挥了巨大的作用；
比较递归与非递归实现：我们用一张表格来比较「递归」和「栈」实现「深度优先遍历」的优缺点。

在实际应用中，相对重要的是代码的可读性和易于维护性。在「力扣」上的绝大多数使用深度优先遍历实现的问题，我们都建议大家采用递归的方式实现。

3. 深度优先遍历的应用

在一些树的问题中，其实就是通过一次深度优先遍历，获得树的某些属性。例如：「二叉树」的最大深度、「二叉树」的最小深度、平衡二叉树、是否 BST。在遍历的过程中，通常需要设计一些变量，一边遍历，一边更新设计的变量的值。

3.1 获得图(树)的一些属性

二叉树的最小深度

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。
二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

int maxDepth(struct TreeNode *root)
{
	int depth1 = 0, depth2 = 0;
	int depth;
	if (root == NULL) {
		return 0;
	}
    // 二叉树的后序遍历求二叉树的最大高度，但这里恰好最上面的根节点就是最大啊深度，所以使用后序遍历来解问题
    depth1 = maxDepth(root->left);    // 左
	depth2 = maxDepth(root->right);   // 右
    depth = 1 + fmax(depth1, depth2); // 根，即处理逻辑, 递下去后加1返回
	return depth;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false；

bool hasPathSum(struct TreeNode *root, int sum)
{
    if (root == NULL) {
        return false;
    }
    sum = sum - root->val;
    return traversal(root, sum);
}
bool traversal(struct TreeNode *root, int sum)
{
    if (root->left == NULL && root->right == NULL && sum != 0) {
		return false;
	}
	// 找到叶子节点，题目要求找叶子节点的路径和，此时判断 sum 是否 == target.
	if (root->left == NULL && root->right == NULL && sum == 0) {
		return true;
	}
	if (root->left != NULL) {
		sum = sum - root->left->val;
		if (traversal(root->left, sum) == true) {
			return true;
		}
		sum = sum + root->left->val;
	}
	if (root->right != NULL) {
		sum = sum - root->right->val; 
		if (traversal(root->right, sum) == true) {
			return true;
		}
		sum = sum + root->right->val; 
	}
	return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

3.2 计算无向图的连通分量

无向图中连通分量的数目

TBD

3.3 检测图中是否存在环

TBD

3.4 二分图检测

TBD

3.5 拓扑排序

课程表

int  **edges;
int  *edgeColSize;
int  *visited;
bool valid;
void dfs(int u) {
    visited[u] = 1;
    for (int i = 0; i < edgeColSize[u]; ++i) {
        if (visited[edges[u][i]] == 0) {
            dfs(edges[u][i]);
            if (!valid) {
                return;
            }
        } else if (visited[edges[u][i]] == 1) {
            valid = false;
            return;
        }
    }
    visited[u] = 2;
}

bool canFinish(int numCourses, int **prerequisites, int prerequisitesSize, int* prerequisitesColSize) {
    valid = true;
    edges = (int **)malloc(sizeof(int *) * numCourses);
    for (int i = 0; i < numCourses; i++) {
        edges[i] = (int*)malloc(0);
    }
    edgeColSize = (int *)malloc(sizeof(int) * numCourses);
    memset(edgeColSize, 0, sizeof(int) * numCourses);
    visited = (int*)malloc(sizeof(int) * numCourses);
    memset(visited, 0, sizeof(int) * numCourses);
    for (int i = 0; i < prerequisitesSize; ++i) {
        int a = prerequisites[i][1], b = prerequisites[i][0];
        edgeColSize[a]++;
        edges[a] = (int*)realloc(edges[a], sizeof(int) * edgeColSize[a]);
        edges[a][edgeColSize[a] - 1] = b;
    }
    for (int i = 0; i < numCourses && valid; ++i) {
        if (!visited[i]) {
            dfs(i);
        }
    }
    for (int i = 0; i < numCourses; i++) {
        free(edges[i]);
    }
    free(edges);
    free(edgeColSize);
    free(visited);
    return valid;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

3.6 回溯算法

4 回溯算法

4.1 概述

在前几节，我们所讲的深度优先搜索都是在树和图上面进行的。接下来，我们来看看深度优先搜索在其他一些实际问题上面的应用

4.2 N皇后问题

4.3 树形问题

回溯算法其实是在一棵隐式的树或者图上进行了一次深度优先遍历，我们在解决问题的过程中需要把问题抽象成一个树形问题。充分理解树形问题最好的办法就是用一个小的测试用例，在纸上画出树形结构图，然后再针对树形结构图进行编码。

重要的事情我们说三遍：画图分析很重要、画图分析很重要、画图分析很重要。

要理解「回溯算法」的递归前后，变量需要恢复也需要想象代码是在一个树形结构中执行深度优先遍历，回到以前遍历过的结点，变量需要恢复成和第一次来到该结点的时候一样的值。

另一个理解回溯算法执行流程的重要方法是：在递归方法执行的过程中，将涉及到的变量的值打印出来看，观察变量的值的变化。

4.4 为什么叫回溯

而「回溯」就是 深度优先遍历 状态空间的过程中发现的特有的现象，程序会回到以前访问过的结点。而程序在回到以前访问过的结点的时候，就需要将状态变量恢复成为第一次来到该结点的值。

在代码层面上，在递归方法结束以后，执行递归方法之前的操作的 逆向操作 即可。

4.5 回溯算法的实现细节

解释递归后面状态重置是怎么回事
当回到上一级的时候，所有的状态变量需要重置为第一次来到该结点的状态，这样继续尝试新的选择才有意义；
在代码层面上，需要在递归结束以后，添加递归之前的操作的逆向操作；
基本类型变量和对象类型变量的不同处理
基本类型变量每一次向下传递的时候的行为是复制，所以无需重置；
对象类型变量在遍历的全程只有一份，因此再回退的时候需要重置；
类比于 Java 中的 方法参数 的传递机制：
基本类型变量在方法传递的过程中的行为是复制，每一次传递复制了参数的值；
对象类型变量在方法传递的过程中复制的是对象地址，对象全程在内存中共享地址。
字符串问题的特殊性
如果使用 + 拼接字符串，每一次拼接产生新的字符串，因此无需重置；
如果使用 StringBuilder 拼接字符串，整个搜索的过程 StringBuilder 对象只有一份，需要状态重置。
为什么不是广度优先遍历
广度优先遍历每一层需要保存所有的「状态」，如果状态空间很大，需要占用很大的内存空间；
深度优先遍历只要有路径可以走，就继续尝试走新的路径，不同状态的差距只有一个操作，而广度优先遍历在不同的层之前，状态差异很大，就不能像深度优先遍历一样，可以 使用一份状态变量去遍历所有的状态空间，在合适的时候记录状态的值就能得到一个问题的所有的解

4.6 练习

全排列

数独

括号生成

5 剪枝

剪枝的想法是很自然的。回溯算法本质上是遍历算法，如果 在遍历的过程中，可以分析得到这样一条分支一定不存在需要的结果，就可以跳过这个分支。

发现剪枝条件依然是通过举例的例子，画图分析，即：通过具体例子抽象出一般的剪枝规则。通常可以选取一些较典型的例子，以便抽象出一般规律

5.1 剪枝技巧例举

5.2 总结

「剪枝」条件通常是具体问题具体分析，因此需要我们积累一定求解问题的经验。

6. 二维平面上的搜索问题(Flood Fill)

6.1 例 1：「力扣」第 79 题：单词搜索（中等）

6.2 例 2：「力扣」第 695 题：岛屿的最大面积（中等）

6.3 练习

6.4 总结

一些二维平面上的问题还可以使用广度优先遍历和并查集实现，大家可以尝试罗列这些问题，并加以练习。