卷积原理（卷积，padding填充，步长，多通道卷积）

1、卷积

卷积可以用于对输入数据进行特征提取，特征提取的过程可以理解为通过卷积对输入特征进行加权运算，提取输入中的重要信息。

卷积运算的过程就是通过卷积核扫描输入矩阵的元素，将卷积核和扫描对应的元素相乘再相加，得到一个输出，通过不断地滑动，得到最后的输出矩阵。其运算过程如下：

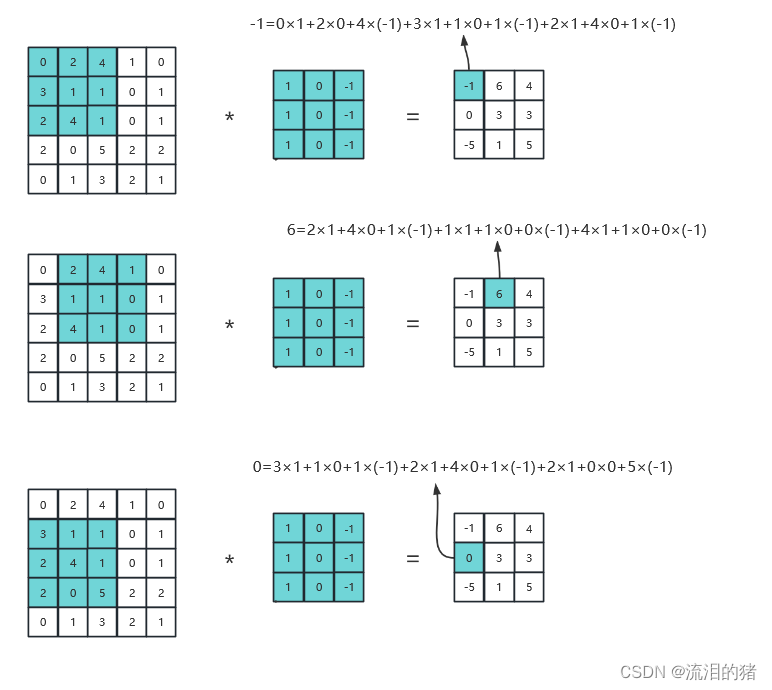
从卷积运算的过程可以看出，输出特征就是输入特征的加权和。

2、Padding

在上边的例子中，采用3×3的卷积核卷积5×5的输入特征矩阵。从上述运算可以看出两个不足。

第一个是通过卷积后输出矩阵相对于输入矩阵变小了，当参与多层的神经网络时，矩阵会变得越来越小。这对于人信息提取是不利的。

第二个是中间元素参与运算的次数要远大于周围元素，尤其是当输入矩阵是高维时，差距会更大，因此在计算中我们会丢失掉一部分的边缘信息。

为了解决以上两点问题，我们在输入矩阵的周围进行填充。

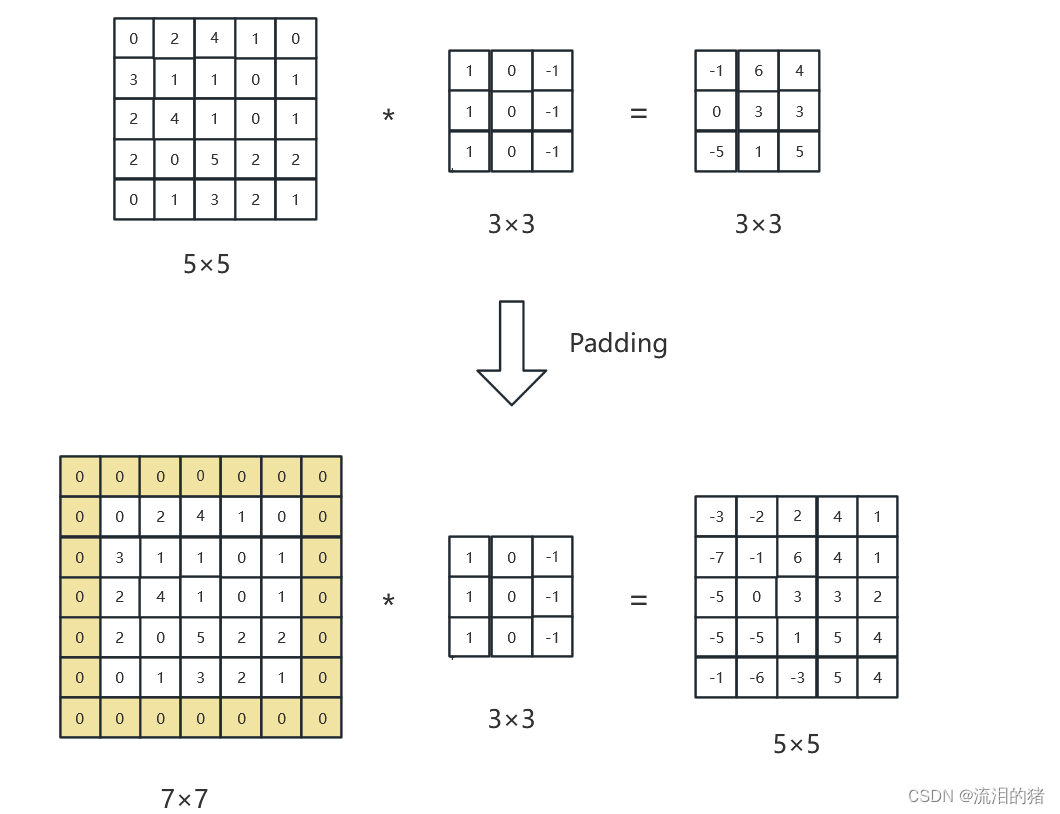
如果输入矩阵的大小是n×n，卷积核的大小是f×f，则输出矩阵的大小为 (n-f+1)×(n-f+1)。

如上图所示，我们在输入矩阵的周边像素周围都填充一个元素，用p表示填充数量，图中展示的填充p为1。

用p表示填充数量，则输出矩阵的大小为（n+2p-f+1）×（n+2p-f+1）

根据填充数量不同，通常有Valid卷积和Same卷积。

valid卷积：不对输入矩阵做填充，即p=0。输出矩阵大小为 (n-f+1)×(n-f+1)

Same卷积：输出矩阵和输入矩阵一样大。即n+2p-f+1=n ，也就是说。

3、卷积步长

在上述用3×3卷积核卷积5×5矩阵的例子中，我们采用的步长s为1，假如将步长s设置为2，则有：

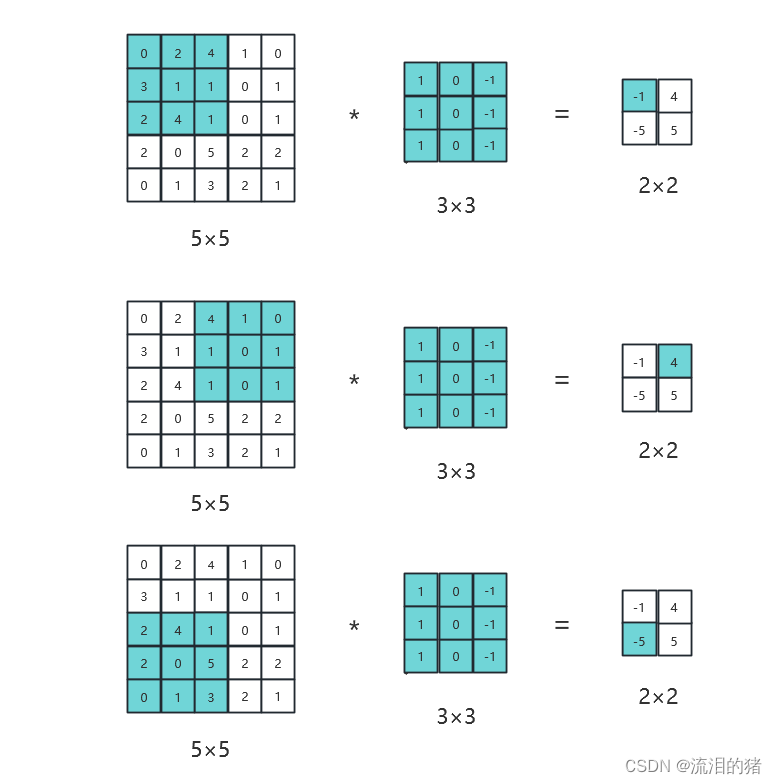
当步长为s，填充数量为p时，输出矩阵的大小为：

n×n       *           f×f       ---->  （）×（）

4、多通道卷积

假设输入数据是多通道的例如彩色图片，有RGB三个通道。针对多通道矩阵，卷积核的通道数应该和输入数据的通道数相同，如下图所示，输入数据是三通道，卷积核也应该是三通道。

 

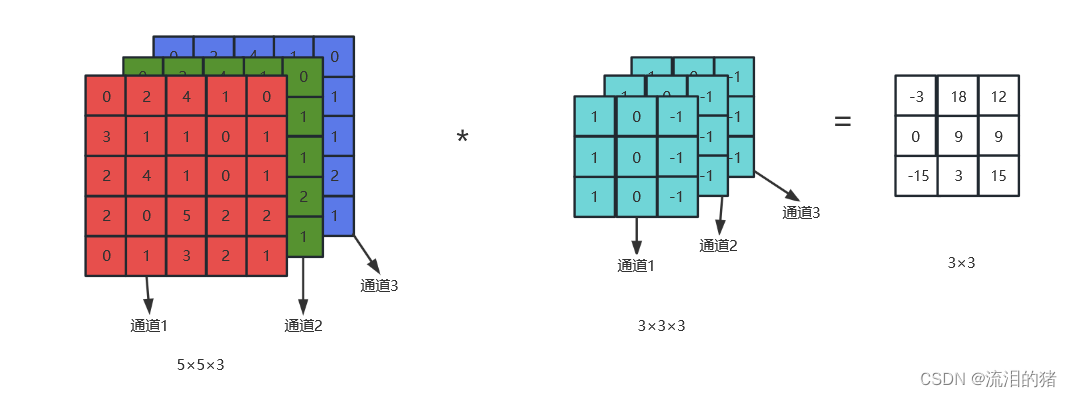
三通道的卷积过程是相应通道的卷积核对相应通道的输入矩阵进行卷积，然后再将结果相加。上述三通道卷积计算过程如下（在这里为了计算简便，将三通道的输入设成一样的）：

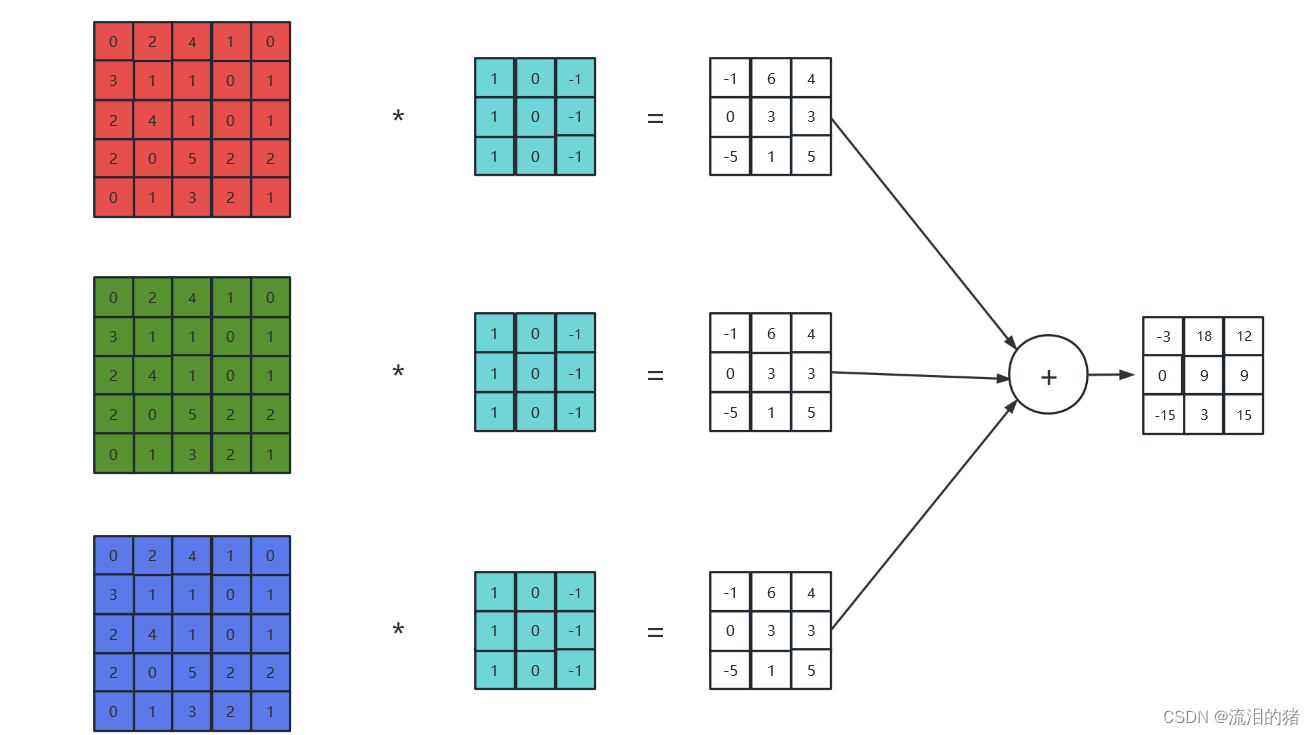
 上述图演示的是只有一个卷积核的卷积过程，如果卷积核有两个，则卷积过程如下：

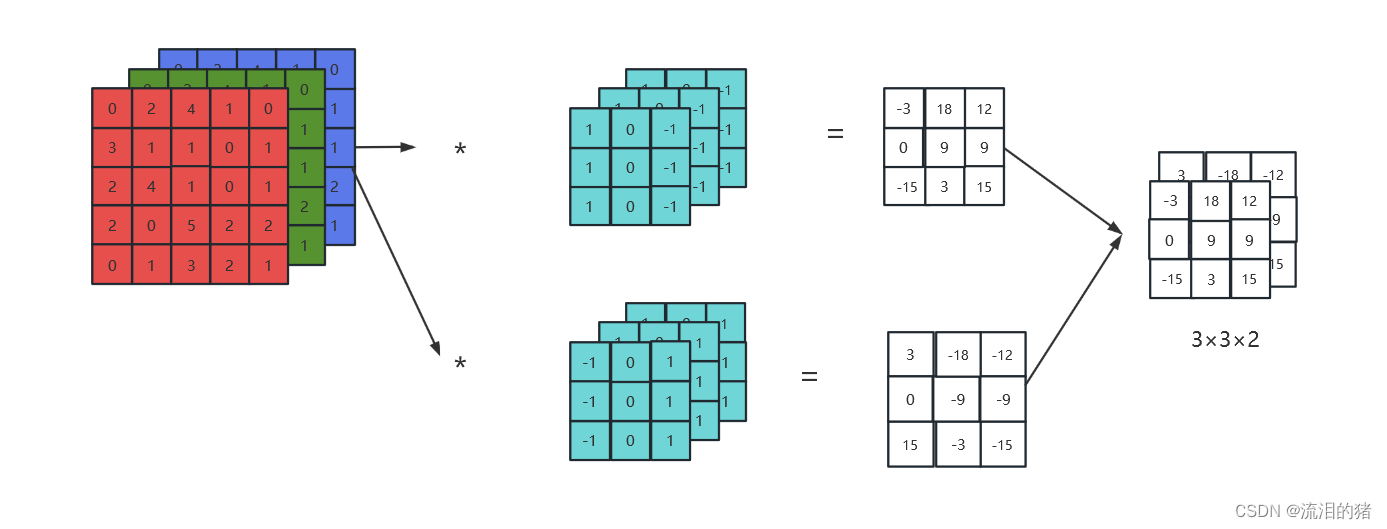
卷积核个数为2则输出矩阵的通道数也为2。

假设输入矩阵通道数为n1，卷积核个数为n2，则输出矩阵为：

n×n×n1       *       f×f×n1      --->         (n-f+1)×(n-f+1)×n2