- 1推荐一款正基AP6255/AP6256代替型号CW2455-44_s912 ap6255
- 2数据结构与算法-顺序表_顺序表的每个元素占8个存储单元
- 3Debezium MySQL源连接器配置属性_inconsistent.schema.handing.mode
- 4一篇文章带你彻底了解【模拟器过检测】_蓝叠过检测
- 5数据结构进阶实训二_看到这一关的任务你是不是想到这样子做呢? for(int i = 0; i< 10; i++){ s
- 6基于Quartus Prime18.1的安装与FPGA的基础仿真(联合Modelsim)教程_intel庐 quartus庐 prime lite edition design software
- 7GPT-4:从纠正错误代码中揭示成熟大模型的涌现能力_大模型代码纠错
- 8西门子1500PLC机器人焊接程序:智能化与高效能的西门子PLC+西门子触摸屏实现的综合控制系统_机器人焊接plc程序
- 9mvn install:install-file maven手动安装第三方jar包报错的一种情况_mvn install:install-file报错
- 10html5边界是什么意思,边界感是什么意思
【排序】插入排序详解(C语言版)
赞
踩
目录
ID:HL_5461
引言
插入排序就像我们平时打扑克牌,拿出从前往后依次拿出一张扑克牌再依次和前面的牌比较,直到找到比它小的将其插入在后面。
这样解释可能不甚明了,大家可以结合下面这张动图来理解(图是网上找的)。
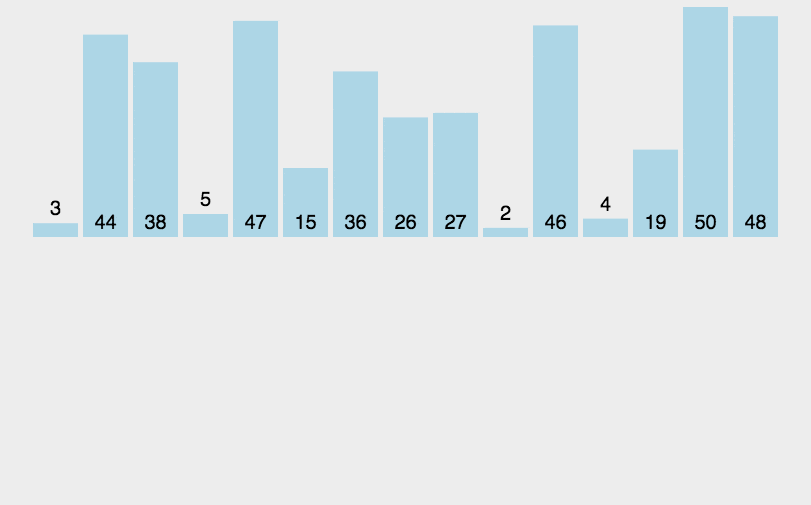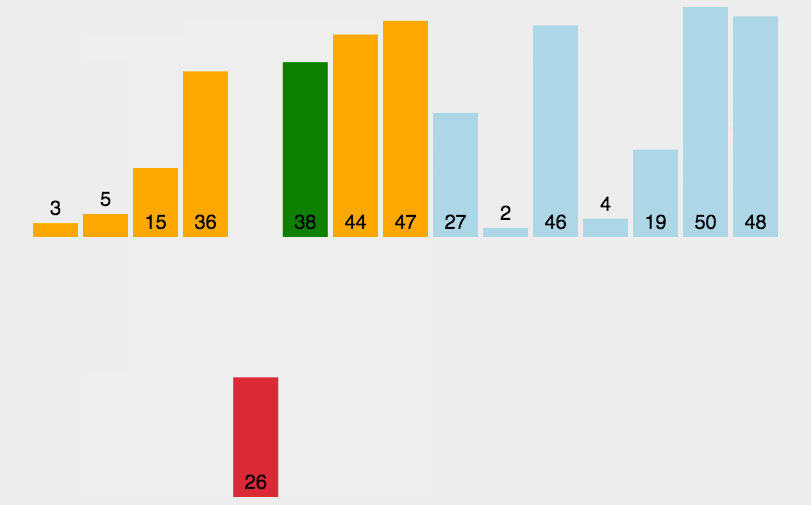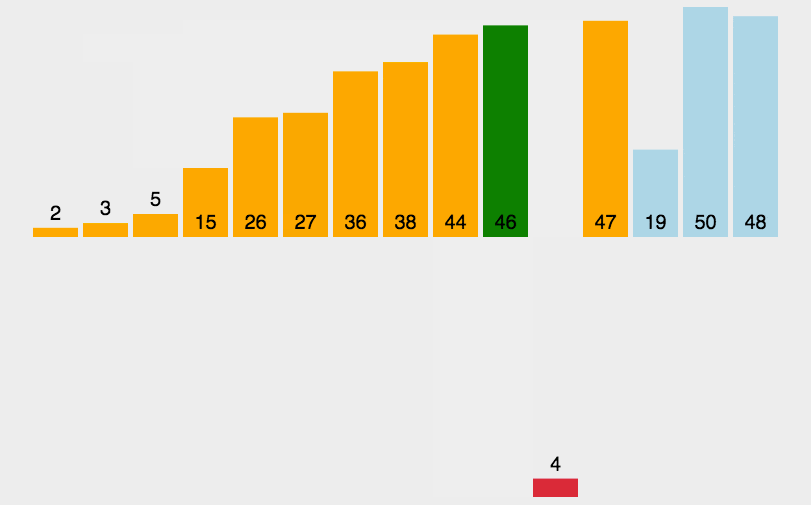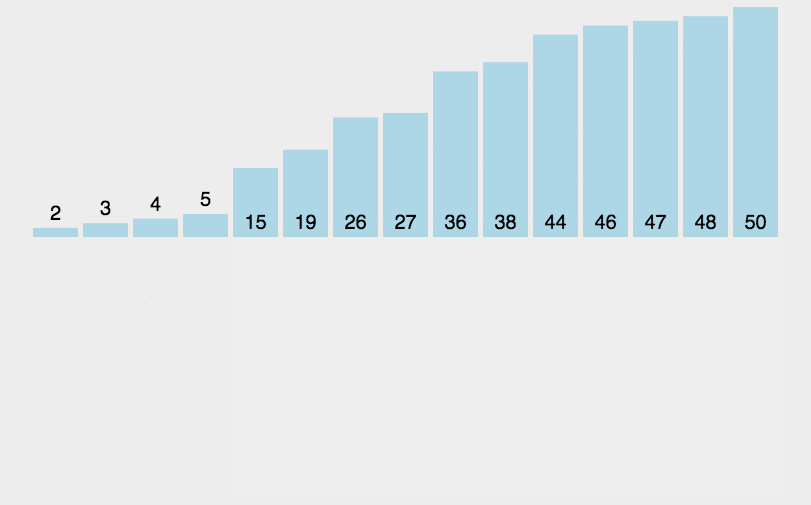
对于插入排序,我们分成直接插入排序(以下简称直插)和希尔排序两部分讲解,全篇以升序为例。OK,现在进入正题!
一、直接插入排序
1.最里层循环
直插的基本思想其实就是无序插入有序,将要排序的数据其实就是一个无序的数组a。
(1)思想
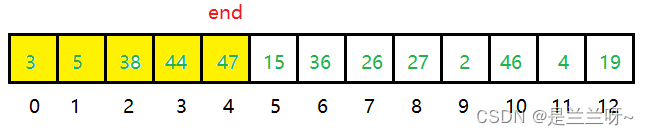
我们假设现在已经完成一部分排序,此时a[0]到a[end]已经有序,我们需要调整a[end+1]。
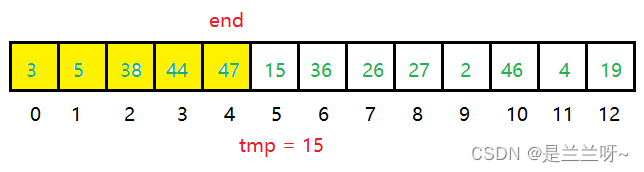
我们先用一个变量tmp保存a[end+1]的值,防止后面的覆盖导致数据丢失。

将tmp的值与a[end]进行比较,如果tmp < a[end],则将a[end]的值覆盖到a[end+1]上面,并将end--。这里我们不难看出之前用tmp保存a[end+1]的意义:因为此时在该数组上,我们已经找不到之前的值了,之前的值已经被覆盖了。
再次比较此时的a[end]与tmp值的大小,tmp < a[end]重复上面操作。

直到tmp >= a[end]。

令a[end+1] = tmp,跳出循环。
你是不是觉得你懂了(听到这句你应该猜到肯定有坑了)。来来来,让我们看一种情况:

如图,tmp为全数组最小的数,我们对它进行如上的移动。

然后,我们就会很快乐地发现这段代码越界了。因为我们之前讨论的跳出循环的条件是tmp >= a[end],而当tmp为全数组最小的数,我们始终无法达到结束条件,只能不断end--。so,由此可见,我们终止循环的条件还是改为end < 0比较好,遇到tmp >= a[end]时再另外break就好。
如果还是不太理解,下面这张流程图希望能帮到你一点。

(2)代码
咱先实现一下这部分代码:
- //这部分代码不全
- int end = 0;//暂时假定end为0
- int tmp = a[end + 1];//保留此时a[end + 1]的值
-
- while (end >= 0)//当还未越界
- {
- if (a[end] > tmp)//比较a[end]与tmp
- {
- a[end + 1] = a[end];//数据后移
- end--;//end下标前移
- }
-
- else//a[end] <= tmp
- {
- break;//end为要插入的前一个数据下标
- }
- }
-
- a[end + 1] = tmp;//tmp的值放入a[end + 1]处

2.最外层循环
(1)思想
外面这层循环的实现要简单的多。
参考上面分析的,我们要将每个数据都进行一次插入排序,每经过一个数据就对它进行上面的操作,所以很显然,最外面这层循环我们只需遍历一遍数组就可以了。
没啥可说的,看代码吧。
(2)代码
- //这里是完整代码
- void InsertSort(int* a, int n)//a为要排的数组,n为数组长度
- {
- for (int i = 0; i < n - 1; i++)//i从下标0开始一直到下标n - 2
- {
- int end = i;
- int tmp = a[end + 1];//保留此时a[end + 1]的值
-
- while (end >= 0)//当还未越界
- {
- if (a[end] > tmp)//比较a[end]与tmp
- {
- a[end + 1] = a[end];//数据后移
- end--;//end下标前移
- }
-
- else//a[end] <= tmp
- {
- break;//end为要插入的前一个数据下标
- }
- }
-
- a[end + 1] = tmp;//tmp的值放入a[end + 1]处
- }
- }

二、希尔排序
1.思想
希尔排序其实就是直接插入排序的优化,也算是插入排序的一种。
希尔排序在直插的基础上进行了一个预处理,来,咱上图看看:
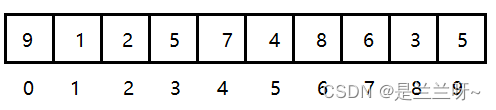
假设如图所示一个无序数组。
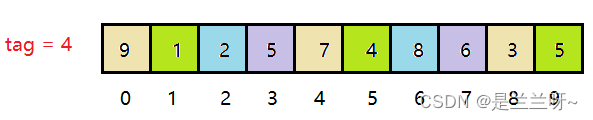
我们将这组数据进行分组,定义一个tag,即每隔tag个数据为一组,如a[n],下一个与它同组的数为a[n+tag],再下一个同组数为a[n+tag+tag],以此推类。
如图,同颜色的为同一组数。
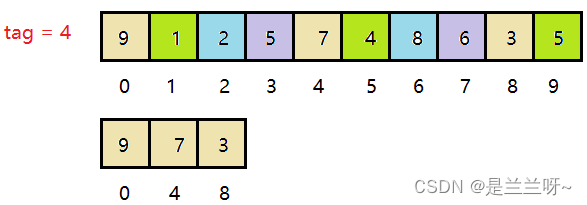
我们将同一组数据进行直插,这里将同一组数据单独放置方便大家观察。

插完之后数组变的部分有序(我知道不明显,先别纠结这个,咱继续)
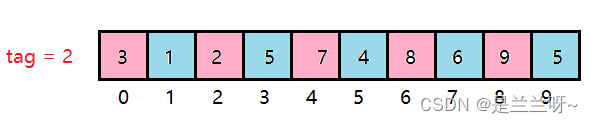
减小tag,再对这个数组进行分组,同色为同一组。
关于tag减小多少合适的问题,我们后面讨论。

我们将每组做一个直插,得到的数据比上一次又更有序了一点。

最后减至tag为1,也就说整个数组为同一组,将每组数据进行直插,等价于将整个数组直接直插。得到有序数组。
我们现在可以讨论讨论tag了:
首先,tag从几开始?
在思考这个问题之前,我们先要明确一点:tag影响了什么?从上述示例我们不难发现,当tag为4时每组2到3个数据,一共有4组;当tag为2时每组5个数据,一共有2组。由此可知,tag越大,每组数据越少,组数越多,反之tag越小,每组数据越多,组数越少。每组有[n/tag,n/tag + 1]个数据(n为数组长度),共有tag组。
OK,可以进入正题看看tag的初始值该为几了。示例中的tag初始值取的是4,但很显然这种取法很不灵活。我们假设两个数组,a1长度为1000000,a2长度为2,我们把4代入。对于a1,我们有250000组,我们设定tag的最初目的就是为了进行预处理,对于这么庞大的组数,显然这样的预处理和我们使用直插法没有什么区别了;对于a2,每组最多有一个数据,而只有一个数据的组很显然是不需要做任何排序的,也就说tag = 4对于a2来说同样不合适。
上述讨论我们不难看出:第一个tag最好是一个与数组长度n相关的可变值,如此,我们不妨将第一个tag取n/2,其中n为数组长度。(当然也有很多不同的取法比如n/3等,这个看个人习惯)
好了,开始第二个问题:tag一次减少多少?
我想肯定很多人第一反应是每次tag--。嗯~怪我前面的示例没举好,那我们再看个栗子~现在假设有一个长度为10000的数组,从tag = n/2开始,每次tag--一直到tag == 1,我们要进行多少次预处理呢?tag == 1时就不算预处理了,也就说去了tag == 1这次,一共有4999次预处理,这还只是一万,那上亿呢?显然,tag--不太现实(CPU:想我死直说,不用拐弯抹角)。那么,咱不仿每次除2吧,这样次数就由n转环为logn了。当然你愿意除3也不是不行,,关于取n/3的坏处我们之后讨论。
最后,关于tag/3的问题。
各位记得我们上面画图讨论的最后一个分组的tag为几吗?1,对吧!现在,我们假定一个数组长度n,取一些n值我们算一算每次的tag:
| n | tag | |||||
| tag/2 | 6 | 3 | 1 | |||
| 21 | 10 | 5 | 2 | 1 | ||
| tag/3 | 6 | 2 | 0 | |||
| 21 | 7 | 2 | 0 | |||
从上面两个例子我们不难发现,如果每次除3我们不一定都有tag == 1,而tag/2却是每次都能保证的。除4除5等也是同样的道理。当然,这个问题可以通过给tag == 1另外写一段代码或是通过使用tag = tag/3 + 1等方法解决,但是有简洁明了的tag = tag/2,我们还是选用简洁一点的方法比较好
我们再回过头看看tag的初始值,我们之前说的是tag = n/2吧,这里我们可以改改,直接令tag = n,然后进入循环,首句为tag = tag/2,这也是同样的效果,这也是我们前面不使用tag = n/3的原因,这样一来,我们就可以把这句直接并入循环了。
再看个流程图加深一下理解:
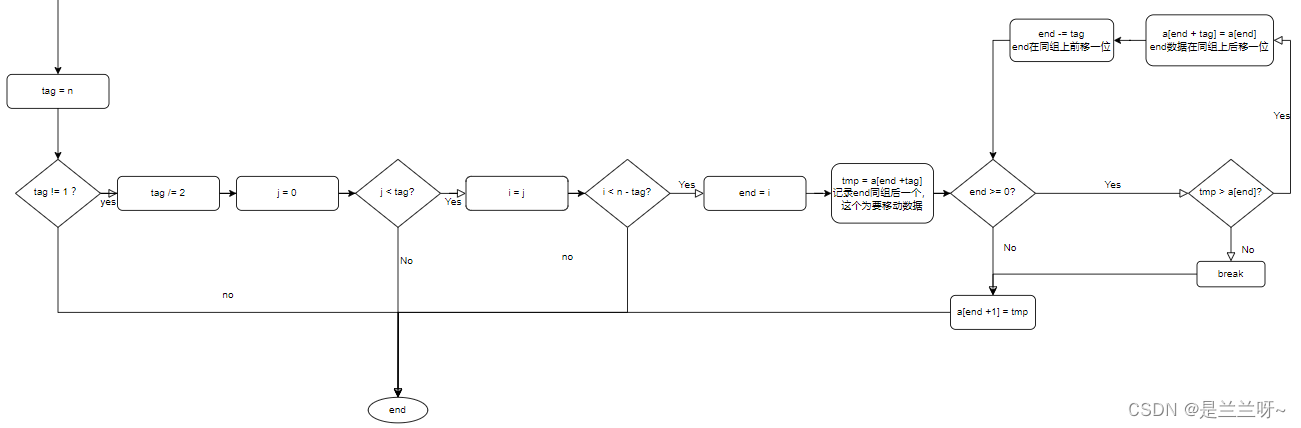
这真的是一个超级超级大的循环。
2.代码
我们先看看直接由前面分析写出的代码:
- void ShellSort(int* a, int n)
- {
- int tag = n;//初始化组数tag为n
-
- while (tag != 1)//不为1,即没有结束最后的直接插入时进入循环
- {
- tag /= 2;//tag减一半
-
- //j为每组第一个数据下标,该层循环为组排序
- for (int j = 0; j < tag; j++)
- {
- //i为组中除最后一个元素的各元素下标,该层循环遍历组中元素,为组中各元素排序
- for (int i = j; i < n - tag; i += tag)
- {
- int end = i;
- int tmp = a[end + tag];//保留此时a[end + tag],即要排数据的值
-
- //该层循环为单个元素的插入排序,将某元素放在合适的位置
- while (end >= 0)
- {
-
- if (a[end] > tmp)//比较a[end]与tmp
- {
- a[end + tag] = a[end];//数据在本组上后移
- end -= tag;//end下标在本组上前移
- }
- else//a[end] <= tmp
- {
- break;//end为要插入的本组前一个数据下标
- }
- }
- a[end + tag] = tmp;//tmp的值放入a[end + tag]处
- }
- }
- }
- }

这循环确实很让人头晕,所以我们不妨对它进行一下优化,将第一个for循环“ for (int j = 0; j < tag; j++) ”去掉,将第二个for循环“ for (int i = j; i < n - tag; i += tag) ”改成“ for (int i = 0; i < n - tag; i++) ”。我们先看看改后的完整代码:
- void ShellSort(int* a, int n)
- {
- int tag = n;//初始化组数tag为n
-
- while (tag != 1)//不为1,即没有结束最后的直接插入时进入循环
- {
- tag /= 2;//tag减一半
-
- //直接遍历但是排序按组
- for (int i = 0; i < n - tag; i++)
- {
- int end = i;
- int tmp = a[end + tag];//保留此时a[end + tag],即要排数据的值
-
- //该层循环为单个元素的插入排序,将某元素放在合适的位置
- while (end >= 0)
- {
-
- if (a[end] > tmp)//比较a[end]与tmp
- {
- a[end + tag] = a[end];//数据在本组上后移
- end -= tag;//end下标在本组上前移
- }
- else//a[end] <= tmp
- {
- break;//end为要插入的本组前一个数据下标
- }
- }
- a[end + tag] = tmp;//tmp的值放入a[end + tag]处
- }
- }
- }

之前那段代码,我们排序是这样优化的直接感受就是现将第一组排完再排第二组,而这段代码则是按照:第一组的第1位、第二组第1位、……、第tag组第1位、第一组的第2位、第二组的第2位、……、第tag组的第2位……这样的循环顺序来排。这样优化的最直观体现就是代码简洁了许多,但要注意,在功能上这段代码和前面是一样的,并没有算法上的优化。
结尾
请停止你离开的脚步,因为我们还没讲完~Let's分析分析直接插入排序和希尔排序的时间空间复杂度还有一些其它乱七八糟的东西。
1.直插和希尔的时间空间复杂度
首先无论是直插还是希尔,我们都没有开辟而外空间,所以它们的空间复杂度毫无疑问都是O(1),不予讨论。下面只讨论时间复杂度。
(1)直接插入
直插我们直接考虑两层循环:一层是遍历数组,由于假定最后一个作为end,再用tmp保存end+1时会出现越界,也就说对于n个元素我们只需遍历n-1个元素就好;再考虑比较的循环,最坏的情况是逆序,每个元素都比现在的第一个元素小,那样对于第二个元素需比较一次,第三个元素需比较2次……第n - 1个元素需比较n - 2次。也就说总共:……
次,由此可得时间复杂度为O(n)。
(2)希尔排序
希尔排序有点复杂,在此不做分析,根据殷人昆的《数据结构-用面相对象方法与C++描述》,暂时就按照到
来算


