常见的激活函数 sigmod Relu tanh LeakyRelu及复现代码_百度自定义leaky_relu激活函数的代码

1.激活函数的作用

关于神经网络中的激活函数的作用，通常都是这样解释：如果不使用激活函数的话，神经网络的每层都只是做线性变换，多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够，所以这时候就体现了激活函数的作用了，激活函数可以引入非线性因素。
在我认为，通俗来说，比如说原先的线性变换能解释类似左图的分类，而无法进行类似右边图像的这种分类

2.sigmod

表达式：

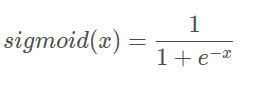
几何图像：

作用：
它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.
缺点：
1：在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。
2：Sigmoid 的 output 不是0均值（即zero-centered）。这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。f(x)=wx+b,若x>0,导致对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。当然了，如果按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的梯度消失问题相比还是要好很多的。
3：其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。
此处参考> https://blog.csdn.net/tyhj_sf/article/details/79932893
代码：

from matplotlib import pyplot as plt
import numpy as np
import math

def sigmoid_function(x):
    fx = []
    for num in x:
        fx.append(1 / (1 + math.exp(-num)))
    return fx

x = np.arange(-10, 10, 0.01)
fx = sigmoid_function(x)

plt.title('Sigmoid')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, fx)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.Relu

表达式：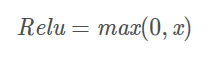
几何图像：

作用：
这个是为了解决梯度消失的问题会出现死亡ReLU问题，计算梯度的时候大多数值都小于0，我们会得到相当多不会更新的权重和偏置。但是死亡ReLU可以带来稀疏性，因为神经网络激活矩阵会有很多0，所以计算成本和效率优化。但是ReLU不能避免梯度爆炸问题****
代码：

import numpy as np
import matplotlib.pylab as plt

def relu(x):
    return np.maximum(0, x)  #输入的数据中选择较大的输出
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)

plt.title('Relu')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4.tanh

表达式：

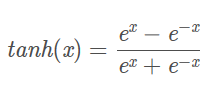
几何图像：
作用：它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。
代码：

import numpy as np
import matplotlib.pylab as plt

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

x = np.arange(-10, 10, 0.1)
p1 = plt.subplot(311)
y = tanh(x)

plt.title('tanh')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

5.LeakyRelu

表达式：

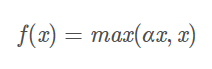
几何图像：

$$\alpha =0.01，左半边斜率接近0，在第三象限$$
作用：
leakyrelu激活函数是relu的衍变版本，主要就是为了解决relu输出为0的问题。如图所示，在输入小于0时，虽然输出值很小但是值不为0。
l缺点：就是它有些近似线性，导致在复杂分类中效果不好。