李宏毅机器学习 ＜Datawhale task3学习笔记＞_datawhale意思

---

---

一、误差从哪里来？

1，Bias

μ：无穷个数据的平均值
m：有限个数据的平均值

n越多时，值应该越集中于μ。

2，Variance

$E[s^2]\ne {\sigma }^2$
由公式，${\sigma }^2$一般略大于$s^2$

bias和variance的区别：（打靶的图非常清晰）
bias很大，距离目标值的偏差越大，目标的位置不正确。
variance很大，数据值就很散，不集中。

二，减小误差

1，variance的场合

不同数据找到的f*都是不一样的，把所有的（100次）实验结果放在一起：

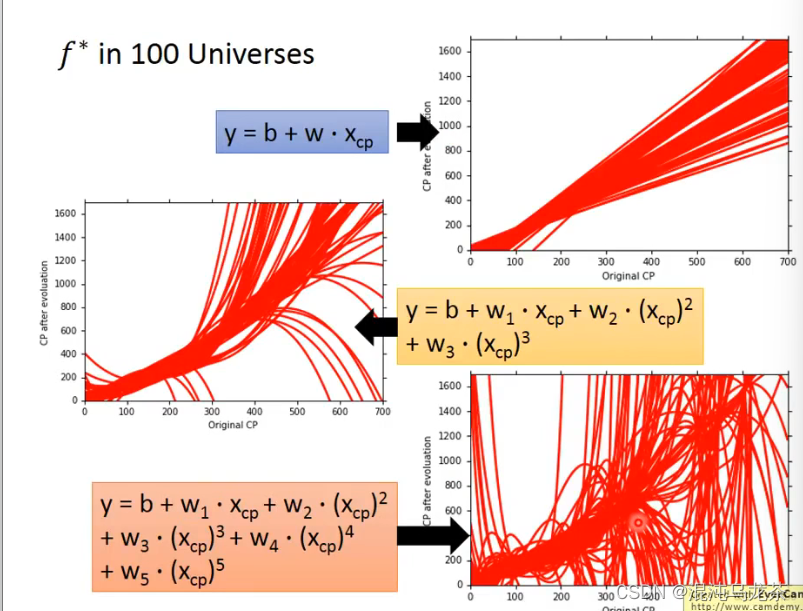
可以发现，高次的模型得到的结果variance很大， 都展开了（？）
对于Variance而言，模型越简单，其variance的值越小，结果越集中。

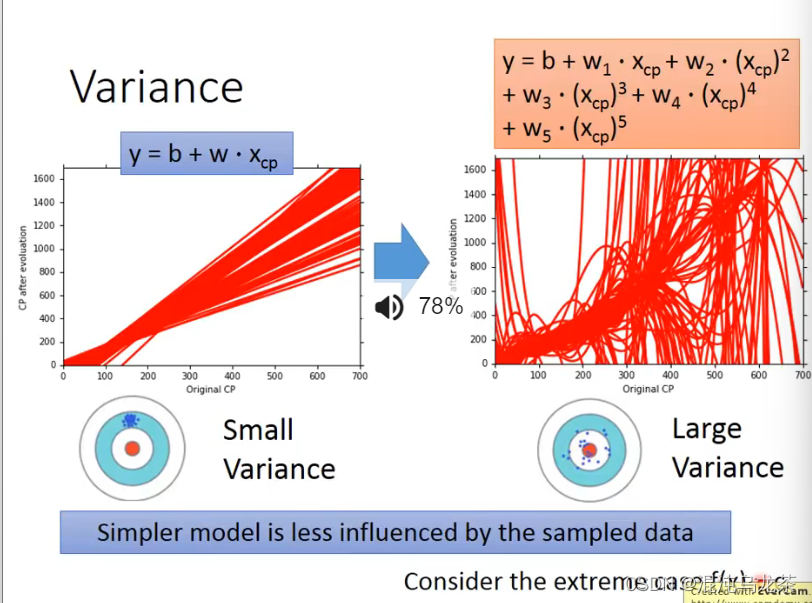
当variance最小时，意思是每一个结果都是一模一样的。其实也不是一个好的结果。

2，bias的场合

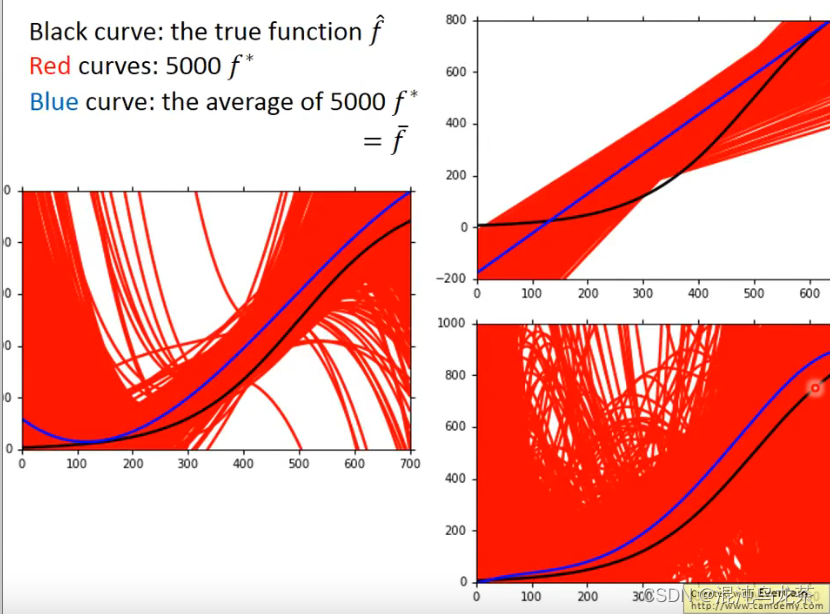
对于bias而言，模型越复杂，得到的平均效果就越好。（观察图像，图中的蓝线和黑线越相似）

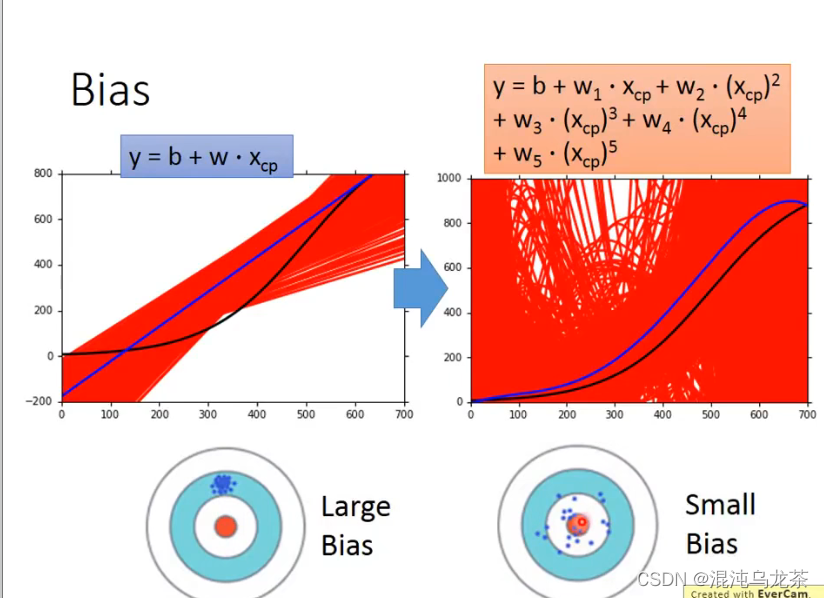
可以发现b和v好像没法两全其美…
（李老师解释：如果model太简单，我们的function set里可能没有我们想要的值，function space可能只是很小一部分。如果model很大，model space也很大，包含目标值的可能性越大。）

我们给这存在这两种误差的模型命名：
如果bias很大，叫做underfitting（欠拟合）
如果variance很大，叫做overfitting（过拟合）

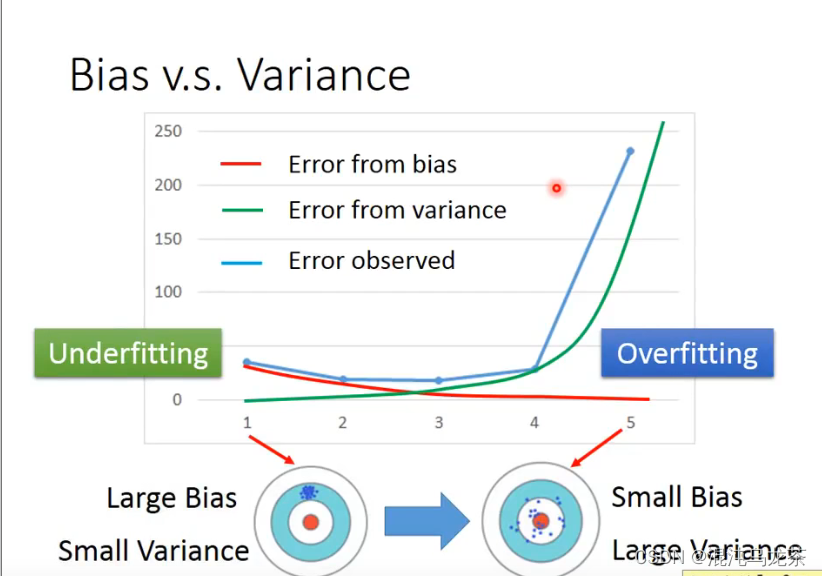
如果欠拟合： 重新设计模型比较好。（没有包含目标，可能是哪里考虑漏了）
如果过拟合： 一种方法是增加training data，但是获得大量data也没那么容易。除了增加data，也可以进行regularization：令曲线越平滑，直接排除掉一些歪七扭八的曲线。但是这也有可能伤害bias，也有一定风险把最佳值直接排除掉。

因此我们在b和v间权衡考虑，选择最好的model。

3，实操时…

一般来讲，真正将模型用到实际，testing set肯定会变化，error会更大。因为实际的时候的数据其实是我们未知的，面对不同的数据function的结果肯定不一样。

实操的时候，可以将数据手动划分成两部分，模拟一个public和private的情况，观察模型error的变化。不建议根据public testing set再重头改model，因为public set也不是最终的结果:)

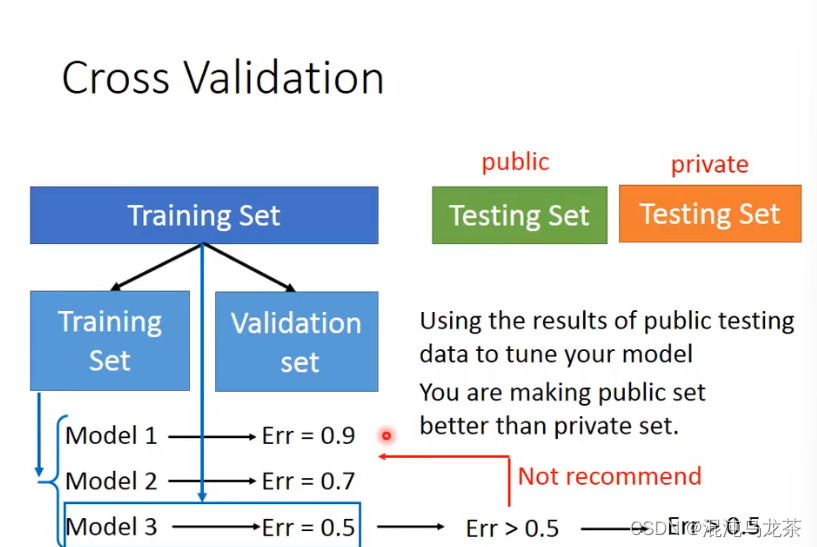
如果担心training set 和validation set的划分可能造成结果可信度差，那也可以考虑将data分成多分，然后轮流拿其中的一份作为validation，分别计算再算model的平均误差。

三，梯度下降

之前学习过，使用梯度下降寻找最好的函数。

用图像表示，是一个动态寻找的过程：

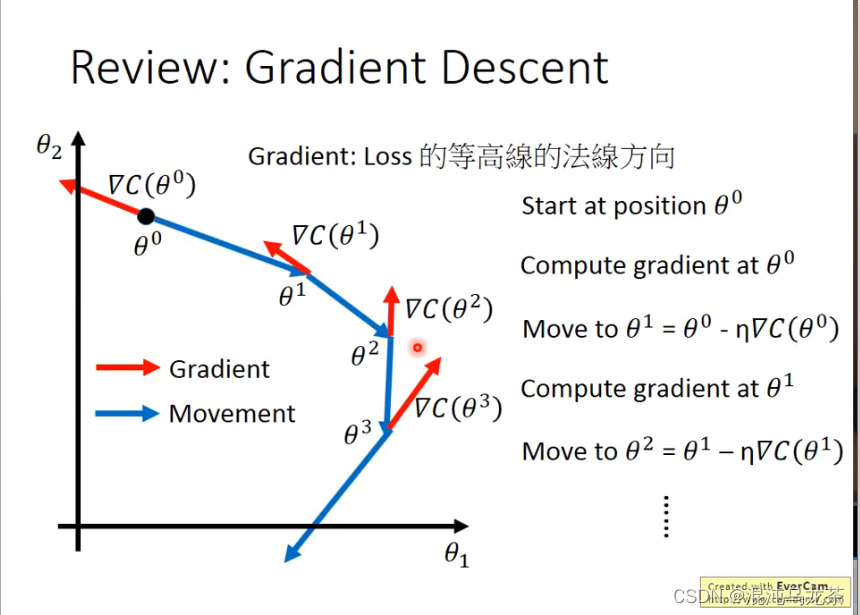
1，注意事项与优化

learning rate 的选取很重要：
太小：速度太慢，效率太低；太大，也有可能错过正确值。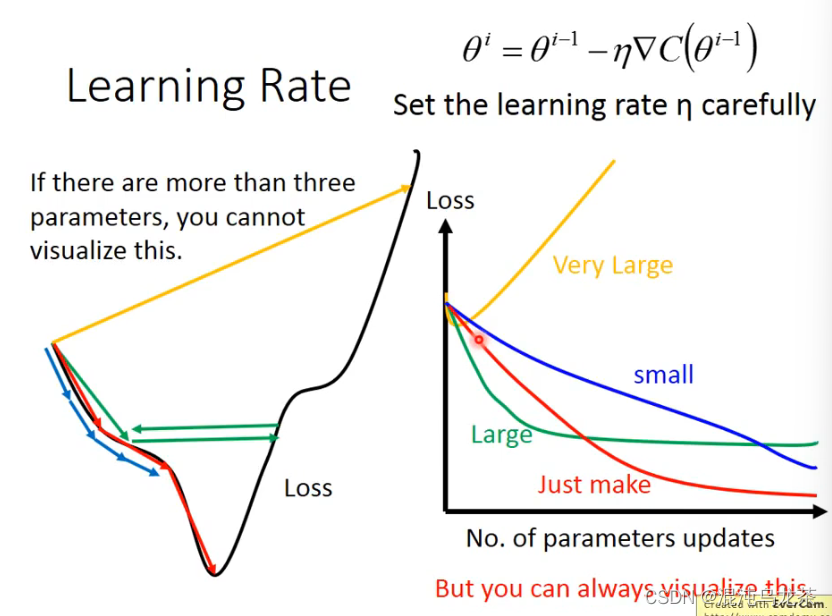
(观察图像：太小loss下降很慢，太大下降到一定程度就不下降了，更更大反而可能loss增加。)

手动调整learning rate比较麻烦。一般来讲，learning rate 随着参数更新会越来越小。比如将learning rate 设计成${\eta }^t=\eta /sqrt(t+1)$
最简单的一种设计方法：Adagrad

①Adagrad

σ相对于每一个w都不一样，具体计算如下图：

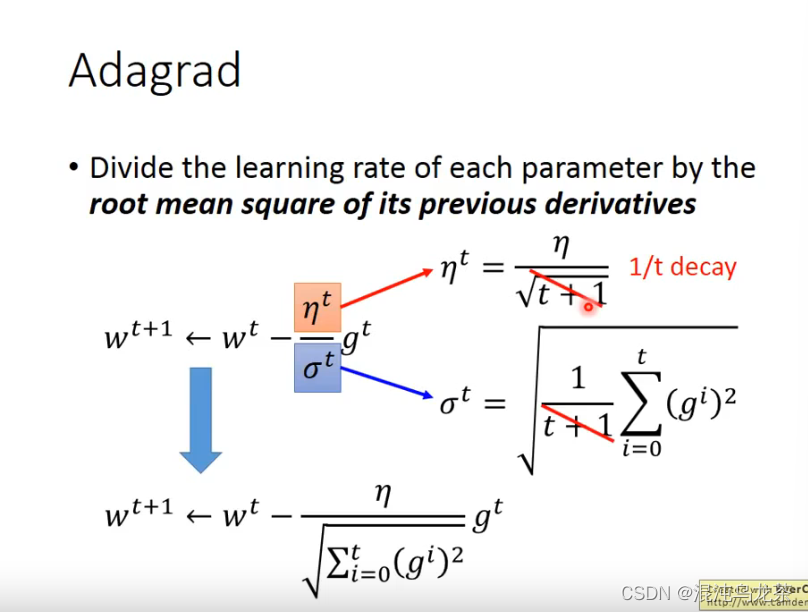
（具体计算时，η和σ可以进行约分，最后的运算还比较简便。)
关于Adagrad的矛盾： 分子的意思是梯度越大，下一步前进的就越多，然而分母是反过来的，梯度越大，下一步前进的反而越少。

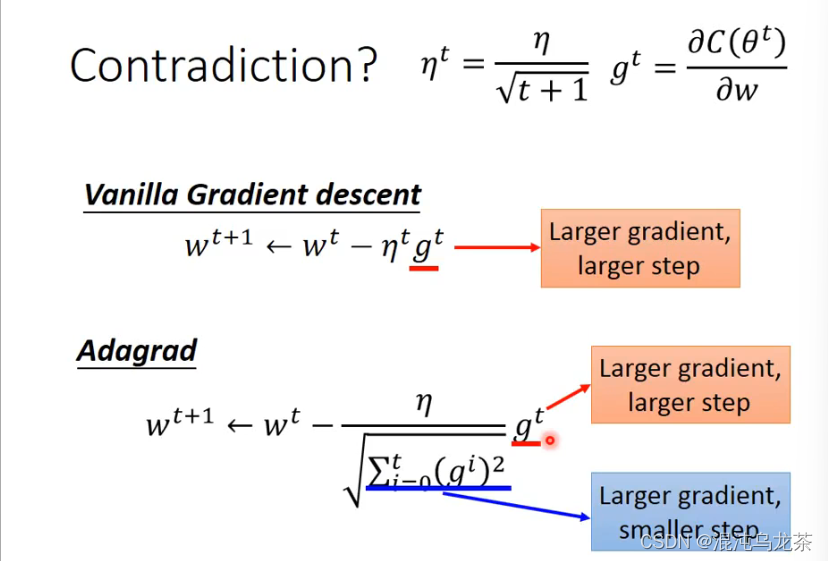
一些解释是：这里的比值反应的是分子分母之间的反差。就是如果有数据突然特别大或者特别小，通过除以之前数据的平方和的方式就可以直观地体现这里数据的变化。

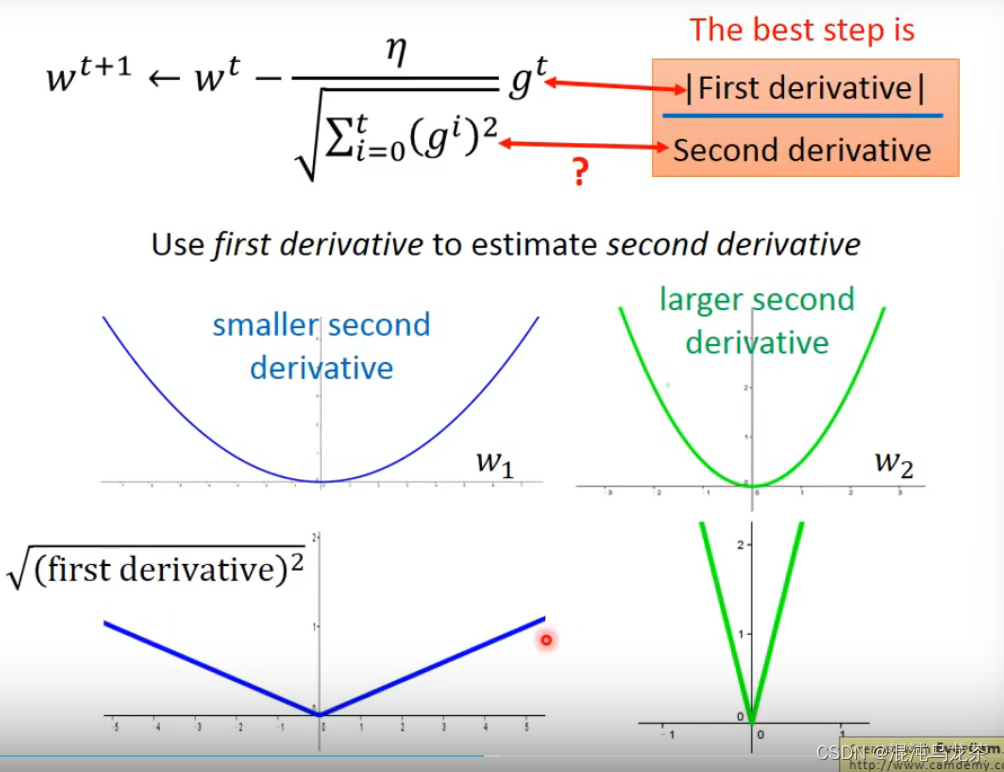
更正式的解释是：当只有单变量时，如果想一步到达最优值处，可以推导出的式子就是这样的。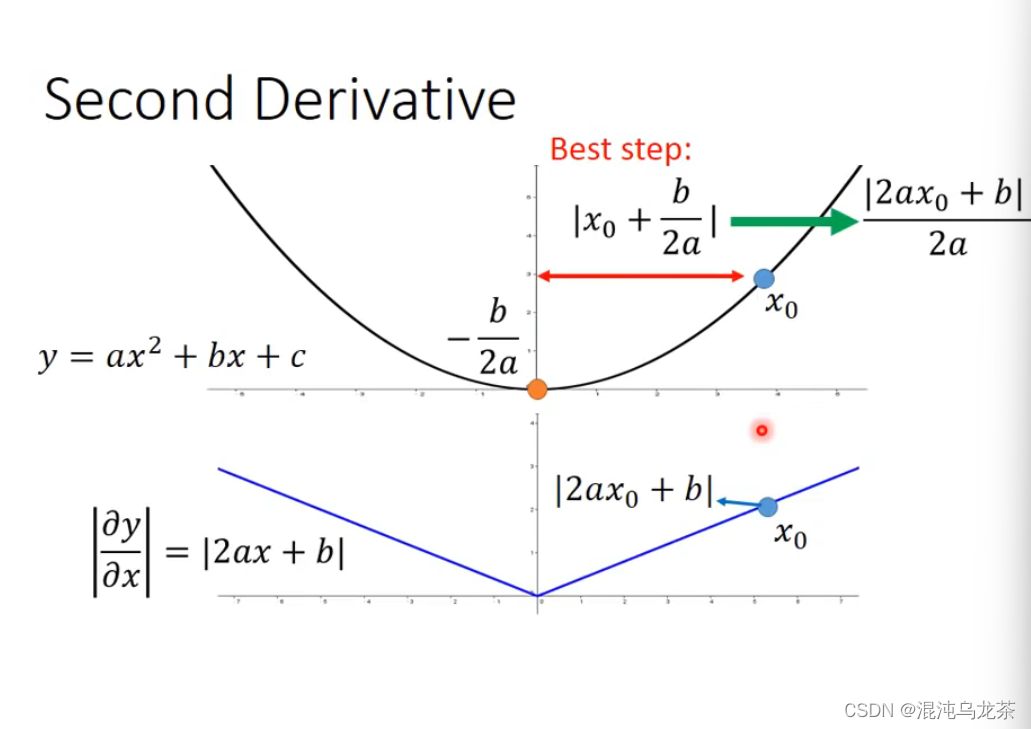
如果想要跨参数的话，比如是在三维时，直接比较一次微分就不太行了（比如这里a的微分小于c的微分，但是a距最低点的距离比c距最低点的距离远），这时候就需要看二次微分。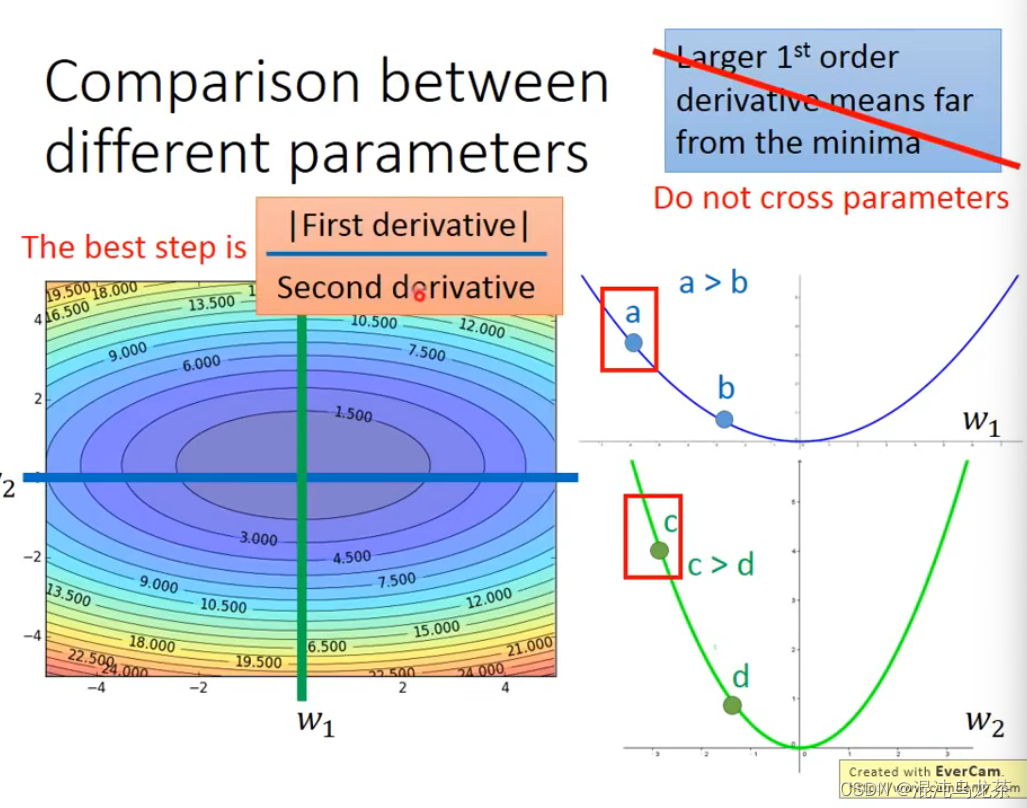
在adagrad中，把之前所有次的微分的平方和开根近似代替二次微分，这样极大减小了运算量。

②stochastic gradient decent（随机梯度下降）

它可以让training速度更快。

图片上面第一个式子是loss function，是要计算所有数据$x_i$ 的loss。
而stochastic gradient descent则是随机取一个$x^n$ ，计算$L^n$ 时只需要考虑选取的这个example的值就可以了。计算次数显而易见地被简化了。

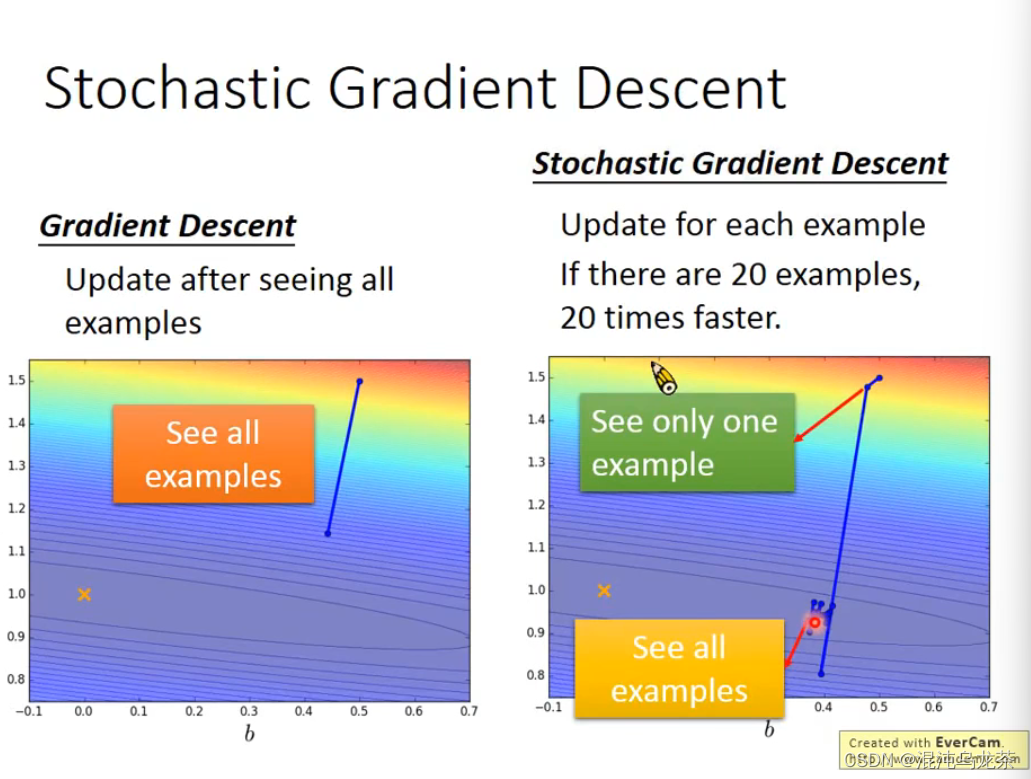
（更快了，也更强了！）

③Feature Scaling

使不同feature的scale尽可能一致。如果值差距过大，大的值对于结果的影响将巨大，而小的值的影响就会特别小（这是显而易见的）。这种时候下w1-w2图像会是一个椭圆型，更新参数会比较困难。
如果值的scale差不多的话，梯度下降的图就更接近圆形，更新的方向也更接近最低点。

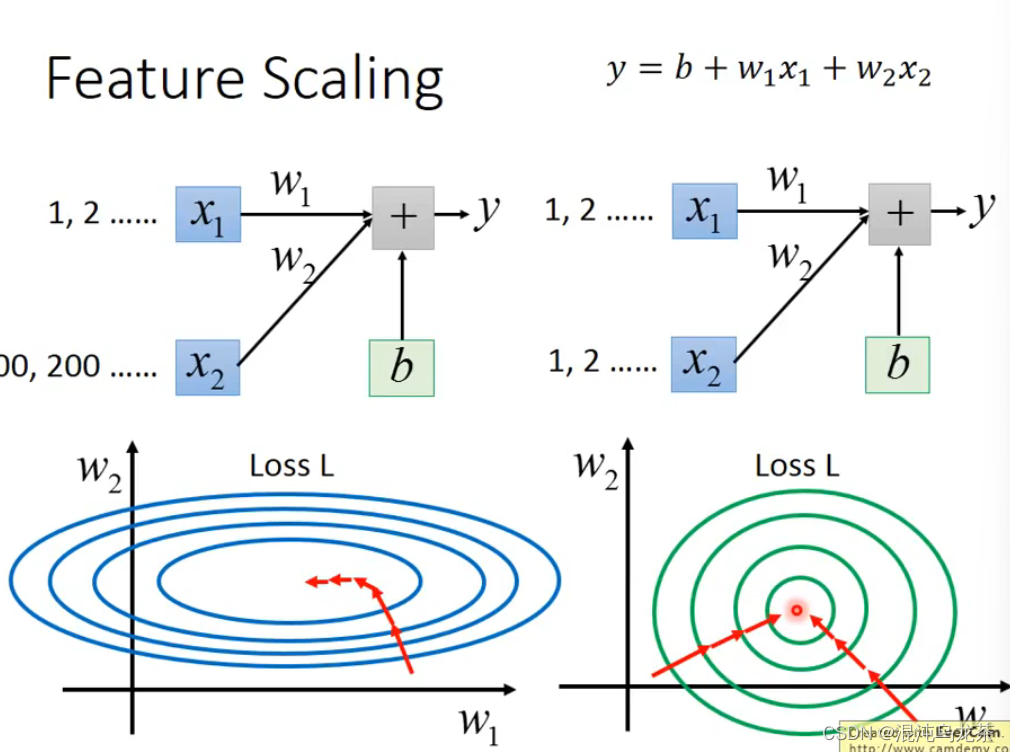
如何做Feature Scaling：最常见的做法如图：

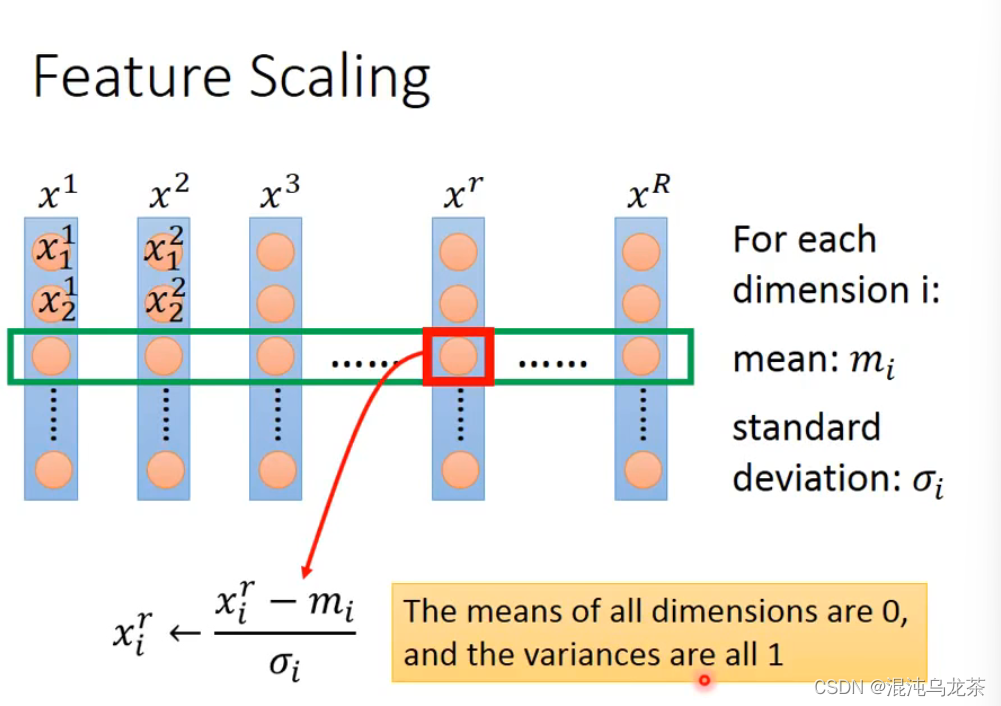
（mean：平均；σ：标准差；给我回去好好学英语 ）

④Formal Derivation

直接找最小值可能不好找。如果有一个点，在这个点边上划定一个区域，那么在这个区域内找到最小值就会简单很多。重复这个过程，将大的范围拆解成小的范围，会好做一些。

根据Taylor Series （泰勒定理）,将式子进行简化，同时把一些量用符号代替：

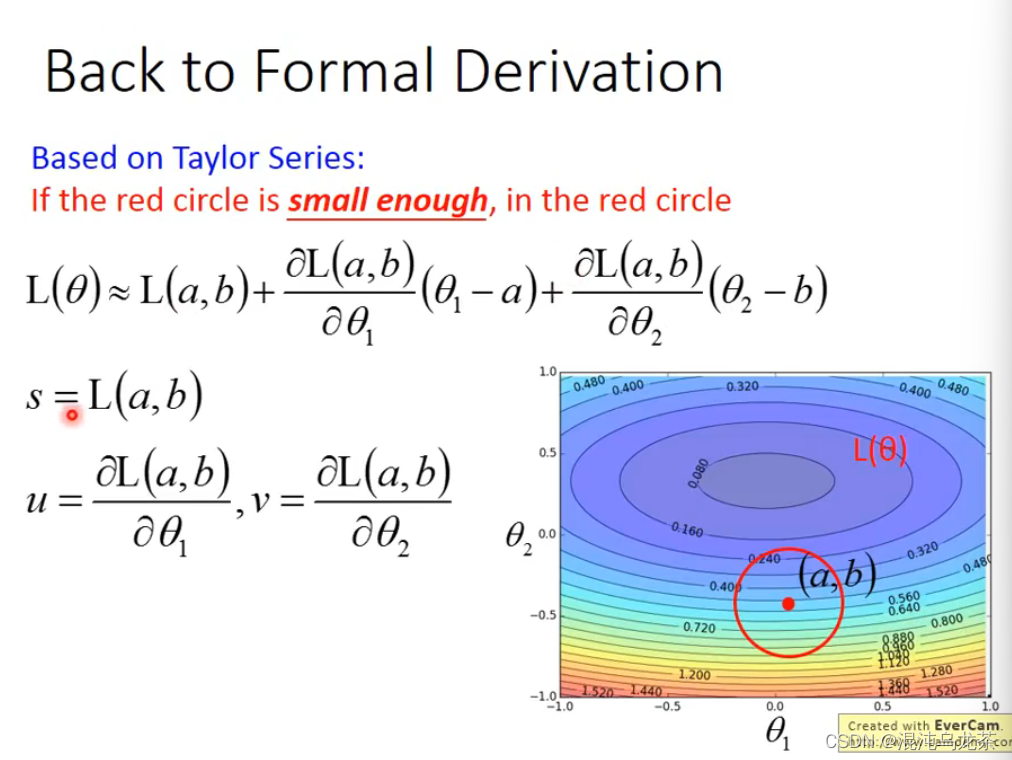
由于是圆内最小的，所以限制坐标在圆内。

因此和learning rate 关系很大！

2，限制

梯度下降仍是主流做法。但是也有很多缺陷：

• 只要微分值=0，就可能会被卡住。
• 微分值接近0的时候，也不一定接近最小值的地方。 对于微分的依赖比较大。