Matlab中filter函数用法_matlab filter

目录

语法

说明

示例

移动平均滤波器

对矩阵行进行滤波

对各部分中的数据进行滤波

有理传递函数

---

        filter函数的功能是对数据进行1 维数字滤波。

语法

y = filter(b,a,x)
 
y = filter(b,a,x,zi)
 
y = filter(b,a,x,zi,dim)
 
[y,zf] = filter(___)

说明

y = filter(b,a,x) 使用由分子和分母系数 b 和 a 定义的有理传递函数对输入数据 x 进行滤波。

如果 a(1) 不等于 1，则 filter 按 a(1) 对滤波器系数进行归一化。因此，a(1) 必须是非零值。

• 如果 x 为向量，则 filter 将滤波后数据以大小与 x 相同的向量形式返回。

• 如果 x 为矩阵，则 filter 沿着第一维度操作并返回每列的滤波后的数据。

• 如果 x 为多维数组，则 filter 沿大小不等于 1 的第一个数组维度进行计算。如果 x 为多维数组，则 filter 沿大小不等于 1 的第一个数组维度进行计算。

y = filter(b,a,x,zi) 将初始条件 zi 用于滤波器延迟。zi 的长度必须等于 max(length(a),length(b))-1。

y = filter(b,a,x,zi,dim) 沿维度 dim 进行计算。例如，如果 x 为矩阵，则 filter(b,a,x,zi,2) 返回每行滤波后的数据。

[y,zf] = filter(___) 还使用任一上述语法返回滤波器延迟的最终条件 zf。

示例

移动平均滤波器

        移动平均滤波器是用于对含噪数据进行平滑处理的常用方法。此示例使用filter函数计算沿数据向量的平均值。创建一个由正弦曲线数据组成的1×100行向量，其中的正弦曲线被随机干扰所损坏。

t = linspace(-pi,pi,100);
rng default  %initialize random number generator
x = sin(t) + 0.25*rand(size(t));

        移动平均值滤波器沿数据移动长度为windowSize的窗口，并计算每个窗口中包含的数据的平均值。以下差分方程定义向量 x 的移动平均值滤波器：

        窗口大小为 5 时，计算有理传递函数的分子和分母系数。

windowSize = 5; 
b = (1/windowSize)*ones(1,windowSize);
a = 1;

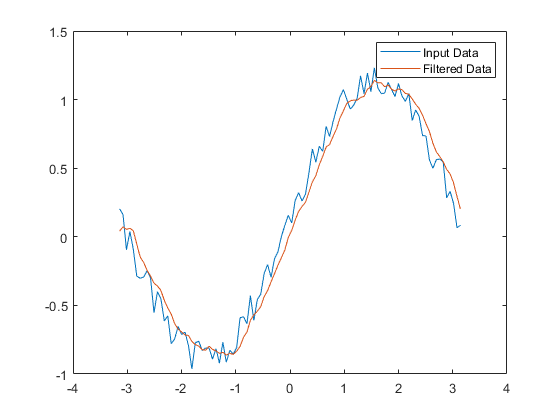
        求数据的移动平均值，并绘制其对原始数据的图。

y = filter(b,a,x);
 
plot(t,x)
hold on
plot(t,y)
legend('Input Data','Filtered Data')

如图所示：

对矩阵行进行滤波

        此示例使用以下有理传递函数对数据的矩阵进行滤波。

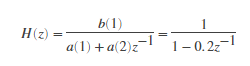
        创建一个由随机输入数据组成的2×15矩阵。

rng default  %initialize random number generator
x = rand(2,15);

        定义有理传递函数的分子和分母系数。

b = 1;
a = [1 -0.2];

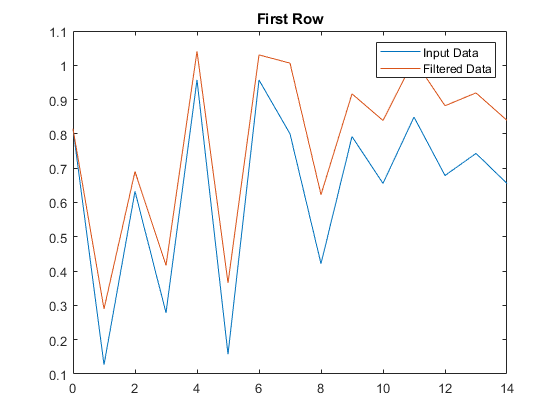
        沿着x的第二维度应用传递函数并返回每行的一维数字滤波结果。绘制原始数据的第一行对已滤波数据的图。

y = filter(b,a,x,[],2);
 
t = 0:length(x)-1;  %index vector
plot(t,x(1,:))
hold on
plot(t,y(1,:))
legend('Input Data','Filtered Data')
title('First Row')

如图所示：

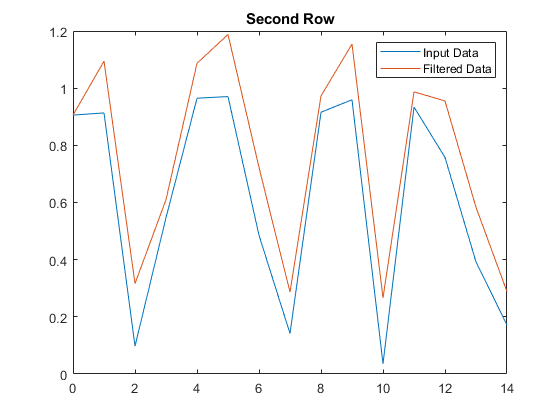
        绘制输入数据的第二行对已滤波数据的图。

figure
plot(t,x(2,:))
hold on
plot(t,y(2,:))
legend('Input Data','Filtered Data')
title('Second Row')

如图所示：

对各部分中的数据进行滤波

        使用滤波器延迟的初始条件和最终条件对各部分中的数据进行滤波，尤其是需要考虑内存限制时请执行此操作。生成一个大型的随机数据序列并将其拆分为两段：x1 和 x2。

x = randn(10000,1);
 
x1 = x(1:5000);
x2 = x(5001:end);

        整个序列 x 是 x1 和 x2 的垂直串联。定义有理传递函数的分子和分母系数，

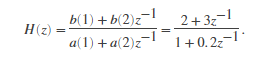
b = [2,3];
a = [1,0.2];

        对子序列 x1 和 x2 进行滤波，一次一个。输出对 x1 进行滤波的最终条件，以便在第一段末尾存储滤波器的内部状态。

[y1,zf] = filter(b,a,x1);

        将对 x1 进行滤波的最终条件用作对第二段也就是 x2 进行滤波的初始条件。

y2 = filter(b,a,x2,zf);

        y1 是来自x1的滤波后的数据，而y2是来自x2的滤波后的数据。整个滤波后的序列是y1和y2的垂直串联。同时对整个序列进行滤波以供比较。

y = filter(b,a,x);
 
isequal(y,[y1;y2])
 
 
ans = logical
   1

b - 有理传递函数的分子系数

        有理传递函数的分子系数，指定为向量。

a - 有理传递函数的分母系数

        有理传递函数的分母系数，指定为向量。

x - 输入数据

        输入数据，指定为向量、矩阵或多维数组。

zi - 滤波器延迟的初始条件

        滤波器延迟的初始条件，指定为向量、矩阵或多维数组。

• 如果 zi 是向量，则它的长度必须是 max(length(a),length(b))-1。

• 如果 zi 是矩阵或多维数组，则主维度的大小必须为 max(length(a),length(b))-1。剩余的每个维度的大小必须与 x 的相应维度的大小匹配。例如，假设沿 3×4×5 数组 x 的第二个维度 (dim = 2) 使用 filter。数组 zi 的大小必须为 [max(length(a),length(b))-1]×3×5。

        由 [] 指定的默认值将所有滤波器延迟初始化为零。

dim - 沿其运算的维度

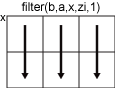
        沿其运算的维度，指定为正整数标量。如果未指定值，则默认值是大小不等于 1 的第一个数组维度。以一个二维输入数组 x 为例。

• 如果 dim = 1，则 filter(b,a,x,zi,1) 沿着 x 的行进行计算并返回应用于每列的滤波器。

  

• 如果 dim = 2，则 filter(b,a,x,zi,2) 沿 x 的列进行计算，并返回应用于每一行的滤波器。

  

  如果 dim 大于 ndims(x)，则 filter 返回 x。

y - 滤波后的数据

        滤波后的数据，以向量、矩阵或大小与输入数组 x 相同的多维数组的形式返回。如果 x 的类型为 single，则 filter 本身以单精度进行计算，y 的类型也是 single。否则，y 以 double 类型返回。

zf - 滤波器延迟的最终条件

        滤波器延迟的最终条件，以向量、矩阵或多维数组的形式返回。

• 如果x是一个向量，则zf是长度为max(length(a),length(b))-1的列向量。

• 如果x是矩阵或多维数组，则 zf 是长度为 max(length(a),length(b))-1的列向量数组，其中zf中的列数等于x中的列数。例如，假设沿3×4×5数组x的第二个维度 (dim = 2) 使用filter。数组zf 的大小为 [max(length(a),length(b))-1]×3×5。

有理传递函数

        Z变换域中这种 filter 运算的输入-输出说明是一种有理传递函数。有理传递函数采用如下形式：

        可同时处理FIR和IIR滤波器[1]。na是反馈滤波器阶数，nb是前馈滤波器阶数。由于归一化，假定a(1) = 1。还可以将有理传递函数表示为以下差分方程：

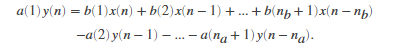
        此外，也可以使用如下图所示的 direct-form II 转置实现表示有理传递函数。此处，na = nb。

        filter在样本 m 处的运算由时域差分方程给定

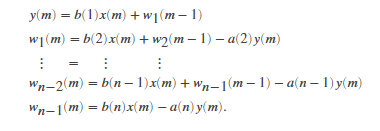
提示

• 如果有 Signal Processing Toolbox™，请将 y = filter(d,x) 与digitalFilter(Signal Processing Toolbox) 对象d结合使用来对输入信号x进行滤波。要根据频率响应设定生成d，可以使用designfilt (Signal Processing Toolbox)。

• 如果有 DSP System Toolbox™，将 y = filter(dObj,x) 与 dfilt (DSP System Toolbox) 对象 dObj 结合使用来对输入信号 x 进行滤波。

• 要将 filter函数与来自 FIR 滤波器的b系数结合使用，请使用 y = filter(b,1,x)。

• 有关滤波函数的详细信息，可以参考数字滤波(Signal Processing Toolbox)。