知新_RL

这个屌丝很懒，什么也没留下！

热门标签

数据挖掘实战分享：财政收入影响因素分析及预测（三）_财政收入影响因素数据挖掘

作者：知新_RL | 2024-03-29 02:30:17

踩

财政收入影响因素数据挖掘

泰迪智能科技（TipDM数据挖掘平台）最新推出的数据挖掘实战专栏

专栏将数据挖掘理论与项目案例实践相结合，可以让大家获得真实的数据挖掘学习与实践环境，更快、更好的学习数据挖掘知识与积累职业经验

专栏中每四篇文章为一个完整的数据挖掘案例。案例介绍顺序为：先由数据案例背景提出挖掘目标，再阐述分析方法与过程，最后完成模型构建，在介绍建模过程中同时穿插操作训练，把相关的知识点嵌入相应的操作过程中。

为方便读者轻松地获取一个真实的实验环境，本专栏使用大家熟知的Python语言对样本数据进行处理以进行挖掘建模。
————————————————
下面进入第三篇，数据模型构建～

灰色预测算

灰色预测法是一种对含有不确定因素的系统进行预测的方法。在建立灰色预测模型之前，需先对原始时间序列进行数据处理，经过数据处理后的时间序列即称为生成列。灰色系统常用的数据处理方式有累加和累减两种。

灰色预测是以灰色模型为基础的，在众多的灰色模型中，GM(1,1)模型最为常用。

设特征

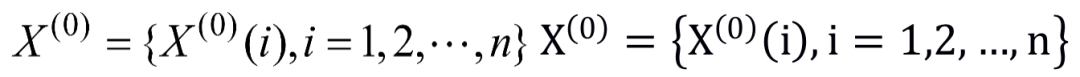
为一非负单调原始数据序列，建立灰色预测模型如下。

（1）首先对X(0)进行一次累加，得到一次累加序列

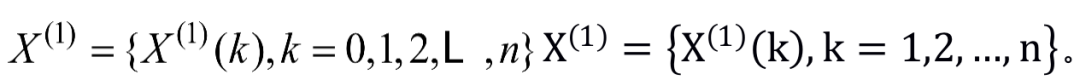
（2）对X(1)可建立下述一阶线性微分方程，如式（1-1）所示，即GM(1,1)模型

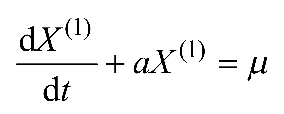
（1-1）

（3）求解微分方程，即可得到预测模型，如式（1-2）所示。

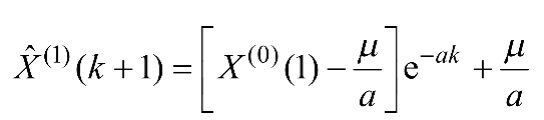
（1-2）

（4）由于GM(1,1)模型得到的是一次累加量，将GM(1,1)模型所得数据

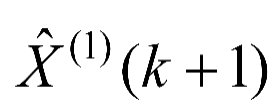
经过累减还原为，即的灰色预测模型如式（1-3）所示。

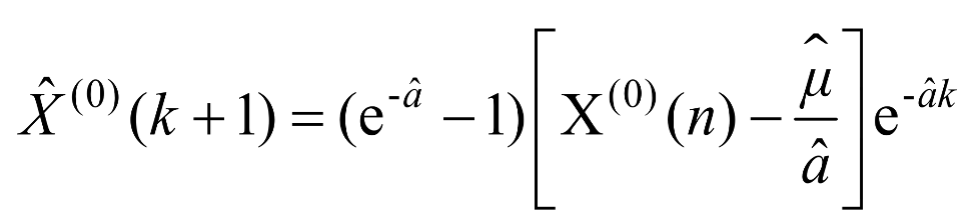
（1-3）

后验差检验模型精度如表1-1所示。

表 1-1后验差检验判别参照表

P	C	模型精度
>0.95	<0.35	好
>0.80	<0.5	合格
>0.70	<0.65	勉强合格
<0.70	>0.65	不合格

灰色预测法的通用性较强，一般的时间序列场合都适用，尤其适合那些规律性差且不清楚数据产生机理的情况。灰色预测模型的优点是具有预测精度高、模型可检验、参数估计方法简单、对小数据集有很好的预测效果。缺点是对原始数据序列的光滑度要求很高，在原始数据列光滑性较差的情况下灰色预测模型的预测精度不高甚至通不过检验，结果只能放弃使用灰色模型进行预测。

SVR算法

SVR（Support Vector Regression，支持向量回归）是在做拟合时，采用了支持向量的思想，来对数据进行回归分析。给定训练数据集

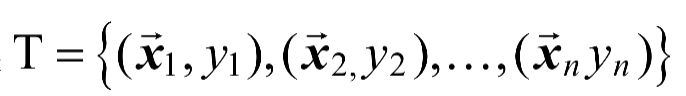
，其中，。对于样本通常根据模型输出与真实值yi之间的差别来计算损失，当且仅当时损失才为零。

SVR的基本思路是：允许

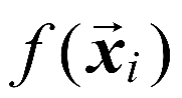
与yi之间最多有ε的偏差。仅当丨时，才计算损失。当时，认为预测准确。用数学语言描述SVR问题如式（1-4）所示。

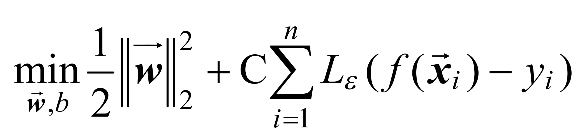
（1-4）

其中

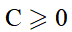
为罚项系数，Lε为损失函数。

更进一步，引入松弛变量

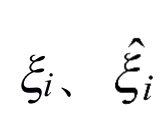
，则新的最优化问题如式（1-5）和式（1-6）所示。

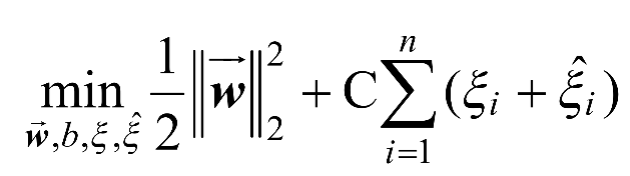
（1-5）

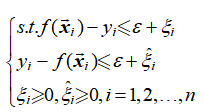
（1-6）

这就是SVR原始问题。类似的，引入拉格朗日乘子，

，定义拉格朗日函数如式（1-7）所示。

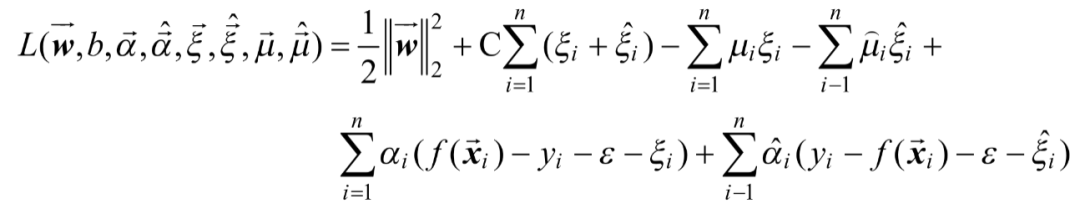
（1-7）

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题，如式（1-8）所示。

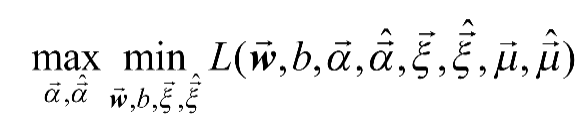
（1-8）

先求极小问题：根据

偏导数可得式（1-9）。

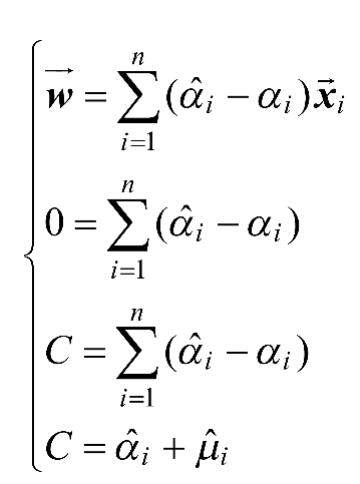
（1-9）

再求极大问题（取负号变极小问题）如式（1-10）和式（1-11）所示。

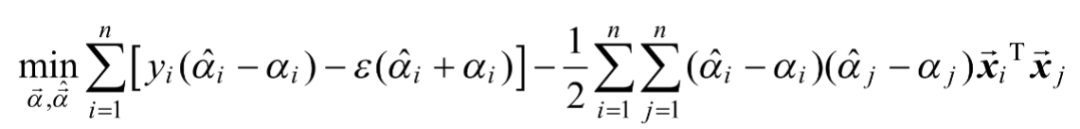
（1-10）

（1-11）

KKT条件如式（1-12）所示。

（1-12）

假设最终解为

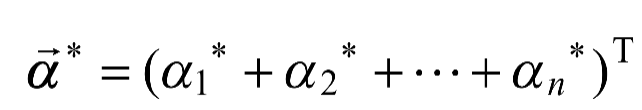
，在中，找出的某个分量，则有式（1-13）和式（1-14）。

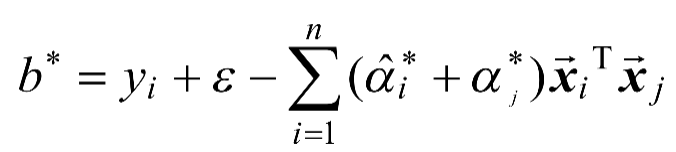
（1-13）

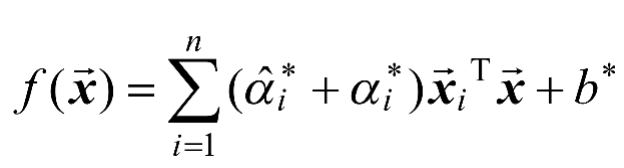
（1-14）

更进一步，如果考虑使用核技巧，给定核函数

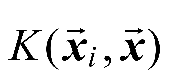
，则SVR可以表示为如式（1-15）所示。

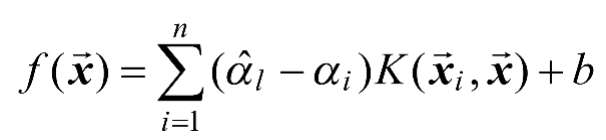
（1-15）

由于支持向量机拥有完善的理论基础和良好的特性，人们对其进行了广泛的研究和应用，涉及分类、回归、聚类、时间序列分析、异常点检测等诸多方面。具体的研究内容包括统计学习理论基础、各种模型的建立、相应优化算法的改进以及实际应用。支持向量回归也在这些研究中得到了发展和逐步完善，已有许多富有成果的研究工作。

相比较于其他方法，支持向量回归优点是：支持向量回归不仅适用于线性模型，对于数据和特征之间的非线性关系也能很好抓住；支持向量回归不需要担心多重共线性问题，可以避免局部极小化问题，提高泛化性能，解决高维问题；支持向量回归虽然不会在过程中直接排除异常点，但会使得由异常点引起的偏差更小。缺点是计算复杂度高，在面临数据量大的时候，计算耗时长。

构建财政收入预测模型

依据Lasso回归选取的关键变量构建灰色预测模型，并预测2014年和2015年的财政收入，如代码清单 1-1所示。

代码清单1-1构建灰色预测模型并预测

import sys

sys.path.append('E/chapter6/demo/code') # 设置路径

import numpy as np

import pandas as pd

from GM11 import GM11 # 引入自编的灰色预测函数

inputfile1 = '../tmp/new_reg_data.csv' # 输入的数据文件

inputfile2 = '../data/data.csv' # 输入的数据文件

new_reg_data = pd.read_csv(inputfile1) # 读取经过属性选择后的数据

data = pd.read_csv(inputfile2) # 读取总的数据

new_reg_data.index = range(1994, 2014)

new_reg_data.loc[2014] = None

new_reg_data.loc[2015] = None

cols = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']

for i in cols:

f = GM11(new_reg_data.loc[range(1994, 2014),i].as_matrix())[0]

new_reg_data.loc[2014,i] = f(len(new_reg_data)-1) # 2014年预测结果

new_reg_data.loc[2015,i] = f(len(new_reg_data)) # 2015年预测结果

new_reg_data[i] = new_reg_data[i].round(2) # 保留两位小数

outputfile = '../tmp/new_reg_data_GM11.xls' # 灰色预测后保存的路径

y = list(data['y'].values) # 提取财政收入列，合并至新数据框中

y.extend([np.nan,np.nan])

new_reg_data['y'] = y

new_reg_data.to_excel(outputfile) # 结果输出

print('预测结果为：\n',new_reg_data.loc[2014:2015,:]) # 预测展示

*代码详见：demo/code/predict.py。

依据灰色预测的结果构建支持向量回归预测模型，并预测2014年和2015年的财政收入，如代码清单 1-2所示。

代码清单1-2 构建支持向量回归预测模型

import matplotlib.pyplot as plt

from sklearn.svm import LinearSVR

inputfile = '../tmp/new_reg_data_GM11.xls' # 灰色预测后保存的路径

data = pd.read_excel(inputfile) # 读取数据

feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13'] # 属性所在列

data_train = data.loc[range(1994,2014)].copy() # 取2014年前的数据建模

data_mean = data_train.mean()

data_std = data_train.std()

data_train = (data_train - data_mean)/data_std # 数据标准化

x_train = data_train[feature].as_matrix() # 属性数据

y_train = data_train['y'].as_matrix() # 标签数据

linearsvr = LinearSVR() # 调用LinearSVR()函数

linearsvr.fit(x_train,y_train)

x = ((data[feature] - data_mean[feature])/data_std[feature]).as_matrix() # 预测，并还原结果

data[u'y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']

outputfile = '../tmp/new_reg_data_GM11_revenue.xls' # SVR预测后保存的结果

data.to_excel(outputfile)

print('真实值与预测值分别为：\n',data[['y','y_pred']])

fig = data[['y','y_pred']].plot(subplots = True, style=['b-o','r-*']) # 画出预测结果图

plt.show()

*代码详见：demo/code/predict.py。

结果分析

对Lasso回归选取的社会从业人数（x1）、社会消费品零售总额（x3）、城镇居民人均可支配收入（x4）、城镇居民人均消费性支出（x5）、全社会固定资产投资额（x6）、地区生产总值（x7）、第一产业产值（x8）和居民消费水平（x13）属性的2014年及2015年通过建立的灰色预测模型得出的预测值，如表1-2所示。

表1-2通过灰色预测模型得出的预测值

变量名	2014预测值	2015预测值	预测精度等级
x1	8142148.2	8460489.3	好
x3	7042.31	8166.92	好
x4	43611.84	47792.22	好
x5	35046.63	38384.22	好
x6	8505523	8627139	好
x7	4600.4	5214.78	好
x8	18686.28	21474.47	好
x13	44506.47	49945.88	好

将表 1-2的预测结果代入地方财政收入建立的支持向量回归预测模型，得到1994年至2015年财政收入的预测值，如表1-3所示，其中y_pred表示预测值。

表 1-3 2014年与2015年财政收入的预测值

年份	y	y_pred	年份	y	y_pred
1994	64.87	37.47637653	2005	408.86	463.4257871
1995	99.75	83.97783525	2006	476.72	555.1990364
1996	88.11	94.64956902	2007	838.99	691.7526587
1997	106.07	106.490953	2008	843.14	843.4121032
1998	137.32	151.1041878	2009	1107.67	1088.474868
1999	188.14	188.14	2010	1399.16	1380.1211
2000	219.91	219.5298325	2011	1535.14	1537.555406
2001	271.91	230.1994976	2012	1579.68	1739.783625
2002	269.1	219.7273221	2013	2088.14	2086.429911
2003	300.55	300.5917203	2014		2189.279622
2004	338.45	383.5338702	2015		2540.638153

地方财政收入真实值与预测值对比图如图 1-1所示。

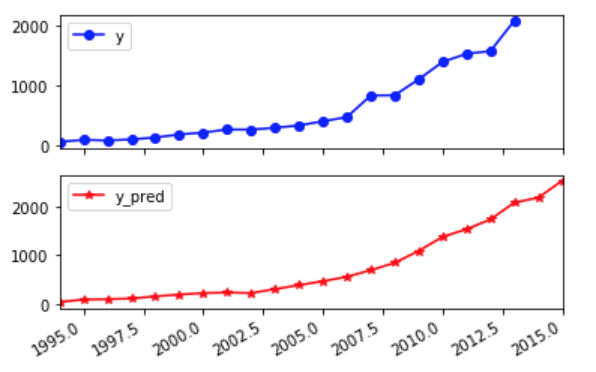
图1-1 地方财政收入真实值与预测值对比图

采用回归模型评价指标对地方财政收入的预测值进行评价，得到的结果如表 1-4所示。

表 1-4 模型评价指标

平均绝对误差	中值绝对误差	可解释方差值	R方值
34.203681	17.415739	0.9908897	0.9908781

由表 1-4可以看出，平均绝对误差与中值绝对误差较小，可解释方差值与R方值十分接近1，表明建立的支持向量回归模型拟合效果优良，可以用于预测财政收入。

下一篇预告：

财政收入影响因素分析及预测模型（四）-上机实验

关注我可了解更多数据挖掘实战知识~ 也可以利用泰迪智能科技 TipDM数据挖掘平台申请试用操作。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/333183