神经网络中的激活函数sigmoid tanh ReLU softmax函数_脉冲神经网络激活函数

神经网络中的激活函数sigmoid tanh ReLU softmax函数

人工神经元简称神经元，是构成神经网络的基本单元，其中主要是模拟生物神经元的结构和特性，接收一组输入信号并产生输出。

一个生物神经元通常具有多个树突和一个轴突。树突用来接收信息，轴突用来发送信息。当神经元所获得的输入信号的积累超过某个阈值的时候，他就处于兴奋状态，产生电脉冲。轴突尾端有许多末梢可以给其他神经元的树突产生链接（突触），并将电脉冲信号传递给其他神经元。

现代神经元中的激活函数通常要求是连续可导的函数。

假设一个神经元接收D个输入$$x_1,x_2,...,x_D$$，令向量$$\mathbf{x}=\left[x_1;x_2;...;x_D\right]$$来表示这组输入，并用净输入（Net Input）$$z\in \mathbb{R}$$表示一个神经元所获得的输入信号$$\mathbf{x}$$的加权和。
$$z=\underset{d=1}{\stackrel{D}{\Sigma }}{\omega }_d{x}_d+b$$

$$={\mathbf{\omega }}^{\mathbf{t}}\mathbf{x}+b$$

其中$$\mathbf{\omega }=\left[{\omega }_1;{\omega }_2;...;{\omega }_D\right]\in {\mathbb{R}}^D$$是D维的权重向量，$$b\in \mathbb{R}$$是偏置。

净输入z在经过一个非线性函数$$f\left(\cdot \right)$$后，得到神经元的活性值a，

$$a=f\left(z\right)$$，

其中非线性函数$$f(\cdot )$$称为激活函数。

激活函数 激活函数在神经元中非常重要的。为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：

1. 连续并可导（允许少数点上不可导）的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。
2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
3. 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

激活函数在深度学习中的作用

激活函数在神经网络中的作用有很多，主要作用是给神经网络提供非线性建模能力。如果没有激活函数，那么再多层的神经网络也只能处理线性可分问题。

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

激活函数有非线性，可微性，单调性，输出值的范围等性质。

选取合适的激活函数对于神经网络有什么样的重要意义

层数比较多的神经网络模型在训练的时候会出现梯度消失(gradient vanishing problem)和梯度爆炸(gradient exploding problem)问题。梯度消失问题和梯度爆炸问题一般会随着网络层数的增加变得越来越明显。梯度消失会使网络训练不动，甚至使模型的学习停滞不前。梯度爆炸一般出现在深层网络和权值初始化值太大的情况下，梯度爆炸会引起网络不稳定，最好的结果是无法从训练数据中学习，而最坏的结果是出现无法再更新的NaN权重值。

例如，一个网络含有三个隐藏层，梯度消失问题发生时，靠近输出层的hidden layer 3的权值更新相对正常，但是靠近输入层的hidden layer1的权值更新会变得很慢，导致靠近输入层的隐藏层权值几乎不变，仍接近于初始化的权值。这就导致hidden layer 1 相当于只是一个映射层，对所有的输入做了一个函数映射，这时此深度神经网络的学习就等价于只有后几层的隐藏层网络在学习。梯度爆炸的情况是：当初始的权值过大，靠近输入层的hidden layer 1的权值变化比靠近输出层的hidden layer 3的权值变化更快，就会引起梯度爆炸的问题。

sigmoid函数

Sigmod型函数是指一类S型曲线函数，为两端饱和函数。常用的Sigmod型函数有Logistic函数和Tanh函数。

饱和对于函数$$f(x)$$，若$$x\to -\infty$$，其导数$$f^{{}^{\prime }}(x)\to 0$$，则称其为左饱和。若$$x\to +\infty$$时，其导数$$f^{{}^{\prime }}(x)\to 0$$，则称其为右饱和。当同时满足左、右饱和时，就称为两端饱和。

Logistic 函数

Logistic函数定义为：

$$\sigma \left(x\right)=\frac{1}{1+\exp \left(-x\right)}$$

Logistic函数可以看成是一个“挤压”函数，把一个实数域的输入“挤压”到（0，1）.当输入值在0附近时，Sigmod型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1.这样的特点也和生物神经元类似，对一些输入会产生兴奋（输出为1），对另一些输入产生抑制（输出为0）和感知器使用的阶跃激活函数相比，Logistic函数是连续可导的，其数学性质更好。

因为Logistic函数的性质，使得装备了Logistic激活函数的神经元具有以下两点性质：1）其输出直接可以看作概率分布，使得神经网络可以更好地和统计学习模型进行结合。2）其可以看作一个软性门（Soft Gate），用来控制其他神经元输出信息的数量。

Tanh函数

Tanh函数也是一种Sigmoid型函数，其定义为：

$$Tanh\left(x\right)=\frac{\exp \left(x\right)-\exp \left(-x\right)}{\exp \left(x\right)+\exp \left(-x\right)}$$

Tanh函数可以看作放大并平移的Logistic函数，其值域是（-1，1）

$$tanh\left(x\right)=2\sigma \left(2x\right)-1$$

下图给出了Logistic和Tanh函数的形状。Tanh函数的输出是零中心化的，而Logistic函数的输出恒大于0.非零中心化的输出会使得最后一层的神经元输入发生偏置偏移，并进一步使得梯度下降的收敛速度变慢

ReLU函数

ReLUctant是目前神经网络中经常使用的激活函数，ReLU实际上是一个斜坡函数，定义为：

Re L U = { x    x ≥ 0 0    x < 0 = max ⁡ ( 0 , x ) \text{Re}LU=\left\{

$$\begin{array}{l} x\ \ x\ge 0\\ 0\ \ x<0\\ \end{array}$$ =\max \left( 0,x \right) \right. ReLU={x  x≥00  x<0​=max(0,x)

**优点：**采用ReLU的神经元只需要进行加、乘和比较的操作，计算上更加高效。ReLU函数也被认为具有生物合理性，比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）。Sigmoid型激活函数会导致一个非疏松的神经网络，而ReLU却具有很好的稀疏性。

在优化方面，相比于Sigmoid型函数的两端饱和，ReLU函数为左饱和，且在x>0时导数为1，在一定程度上缓解了神经网络的梯度消失的问题，加速梯度下降的收敛速度。

**缺点：**ReLU函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。此外，ReLU神经元在训练时容易”死亡“。在训练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU神经元在所有训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活

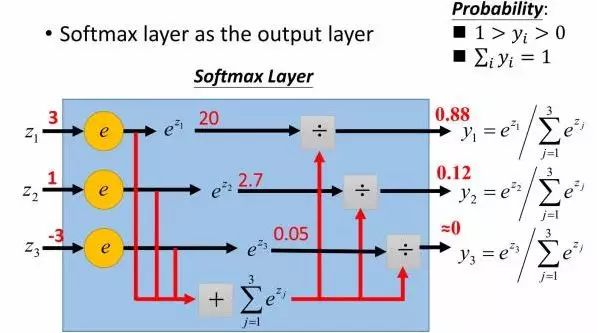
softmax()激活函数

在二分类任务中，输出层使用的激活函数为 sigmoid，而对于多分类的情况，就需要用到softmax 激活函数给每个类都分配一个概率。多分类的情况下，神经网络的输出是一个长度为类别数量的向量，比如输出是(1,1,2)，为了计算概率，可以将其中的每个除以三者之和，得到 (0.25, 0.25, 0.5)。
但是这样存在一个问题，比如像 (1,1,-2) 这种存在负数的情况，这种方法就不行了。解决办法是先对每个元素进行指数操作，全部转换为正数，然后再用刚才的方法得到每个类别的概率。softmax 函数将每个单元的输出压缩到 0 和 1 之间，是标准化输出，输出之和等于 1。softmax 函数的输出等于分类概率分布，显示了任何类别为真的概率。softmax 公式如下
$$\sigma \left(z^i\right)=\frac{e^{z_i}}{{\Sigma }_{j=1}^N{e}^{z_i}}$$

import math
from matplotlib import pyplot as plt
import numpy as np
 
def softmax(x):
    return np.exp(x)/np.sum(np.exp(x), axis=0)
 
def sigmoid(x):
    return 1. / (1 + np.exp(-x))
 
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
 
def relu(x):
    return np.where(x < 0, 0, x)


def plot_softmax():
    x = np.linspace(-10, 10, 200)
    y = softmax(x)
    plt.plot(x, y, label="softmax", linestyle='-', color='blue')
    plt.legend()
    plt.savefig("softmax.png")
    #plt.show()
 
def plot_sigmoid():
    fig = plt.figure()
    ax = fig.add_subplot(111)
    x = np.linspace(-10, 10)
    y = sigmoid(x)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.spines['bottom'].set_position(('data', 0))
    ax.set_xticks([-10, -5, 0, 5, 10])
    ax.yaxis.set_ticks_position('left')
    ax.spines['left'].set_position(('data', 0))
    ax.set_yticks([-1, -0.5, 0.5, 1])
    plt.plot(x, y, label="Sigmoid", linestyle='-', color='blue')
    plt.legend()
    plt.savefig("sigmoid.png")
    #plt.show()
 
def plot_tanh():
    x = np.arange(-10, 10, 0.1)
    y = tanh(x)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_position(('data', 0))
    ax.spines['bottom'].set_position(('data', 0))
    ax.plot(x, y, label="tanh", linestyle='-', color='blue')
    plt.legend()
    plt.xlim([-10.05, 10.05])
    plt.ylim([-1.02, 1.02])
    ax.set_yticks([-1.0, -0.5, 0.5, 1.0])
    ax.set_xticks([-10, -5, 5, 10])
    plt.tight_layout()
    plt.savefig("tanh.png")
    #plt.show()
 
def plot_relu():
    x = np.arange(-10, 10, 0.1)
    y = relu(x)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_position(('data', 0))
    ax.plot(x, y, label="relu", linestyle='-', color='blue')
    plt.legend()
    plt.xlim([-10.05, 10.05])
    plt.ylim([0, 10.02])
    ax.set_yticks([2, 4, 6, 8, 10])
    plt.tight_layout()
    plt.savefig("relu.png")
    #plt.show()
 
 
if __name__ == "__main__":
    plot_softmax()
    plot_sigmoid()
    plot_tanh()
    plot_relu()
   
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86