VMD为什么需要进行参数优化，最小包络熵，样本熵，排列熵，信息熵，适应度函数到底该选哪个_参数优化vmd

“ 之前写过很多智能算法优化VMD的文章，但是并没有对优化VMD所选的适应度函数进行过多介绍，今天在这篇文章会结合相关文献分别介绍一下，VMD参数为何需要优化，以及优化的话到底该选择哪种适应度函数作为自己的优化目标。”

01

—

VMD参数优化的必要性

VMD分解信号前需要设置合适的模态个数K和惩罚参数α，K取值过大会导致过分解，反之，则会欠分解，α 取值过大，会造成频带信息丢失，反之，会信息冗余，所以需要确定最佳参数组合[K，α]。目前多用中心频率观察法，通过观察不同K值下的中心频率确定K值，但该法具有偶然性，且只能确定模态个数K，无法确定惩罚参数α。在《基于参数优化 VMD 和样本熵的滚动轴承故障诊断》这篇文献中，详细介绍了在不同的K和α值对VMD分解的影响。大家可以根据文献自行学习。

参考文献：刘建昌,权贺,于霞,等.基于参数优化 VMD 和样本熵的滚动轴承故障诊断[J].自动化学报, 2022, 48(3):12.DOI:10.16383/j.aas.c190345.

02

—

适应度函数选择+文献介绍

目前，关于适应度函数的选取大致有四种，后期如果发现了新的，或者大家又发现新的都可以后台告诉我一下，后期的代码种也会陆续更新，这篇文章先给大家整理四种适应度函数，并附上各自的参考文献。

1.最小包络熵为适应度函数

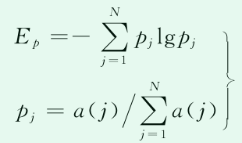
    以包络熵极小值作为适应度函数，包络熵代表原始信号的稀疏特性，当IMF中噪声较多，特征信息较少时，则包络熵值较大，反之，则包络熵值较小。这也是绝大多数文献的做法。这里作者就选一篇经典文献作为参考。

参考文献：唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(05):73-81.

2.最小信息熵为适应度函数

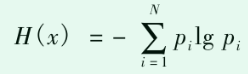
    信息熵是描述系统不确定程度的物理量。当概率 分布P的不确定度越大时，其对应的熵值就会越大;反 之，当P的不确定度越小时，其熵值也越小。因此，若分解得到的IMF包含故障信息，由于周期冲击的缘故，其表现地越有序，导致熵值小。

参考文献：李华,伍星,刘韬,陈庆.基于信息熵优化变分模态分解的滚动轴承故障特征提取[J].振动与冲击,2018,37(23):219-225.

3.最小排列熵为适应度函数

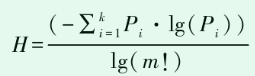
文献原话为：为能准确找到[k,α]的最佳组合，优化函数选取归一化排列熵，排列熵值可以有效反映时间序列的复杂程度，排列熵经过归一化处理后可以更好地反映时间序列的规则程度。排列熵越小说明时间序列越 规则；反之，时间序列的随机性越强。

参考文献：刘宇鹏,赵文卓,邹英永.基于优化VMD与BP神经网络结合的滚动轴承故障诊断方法研究[J].吉林工程技术师范学院学报,2023,39(01):91-96.

4.最小样本熵为适应度函数

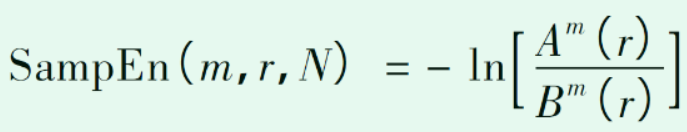
文献原话为：样本熵（sample entropy）的物理含义与近似熵相似，它是用来测量信号中出现新模式的概率，并测量其复杂性。随着新模型生成的可能性增加，这个时间序 列就变得更加复杂。样本熵的优点是计算结果与数据的长度无关，其计算式的参数中m和r对样本熵影响 程度是一致的，因此样本熵拥有更好的一致性。对于信号数据而言，样本熵值越低，则其样本序列自我相似度愈高；反之，其样本序列便越复杂。

参考文献：李颖,王鹏,吴仕虎,巴鹏.基于AO-VMD的往复压缩机故障特征提取方法[J].机电工程,2023,40(05):673-681.

其实每个方法都是有理论依据的，具体选用哪个作为适应度函数，这个需要大家自行实验，自行斟酌。只要最后能够达到自己的目的即可。

关注下方小卡片，获取更多代码资源。