Flutter 绘制番外篇 - 圆中取形

前言：

对一些有趣的绘制 技能和知识， 我会通过 [番外篇]的形式加入《Flutter 绘制指南 - 妙笔生花》小册中，一方面保证小册的“与时俱进” 和 “活力”。另一方面，是为了让一些重要的知识有个 好的归宿。

---

一、正 N 边形的绘制

1. 正三角形绘制

对于正 N 形而言，绘制的本质就是对点的收集。如下图，外接圆上，平均等分三份，对应弧度的圆上坐标即为待收集的点。将这些点依次相连，即可得到期望的图形。

---

容易看出，对于正三角形，三个点分别位于 0°、120°、240° 的圆上。通过 三角函数更新很容易求得三个点的坐标，并用 points 列表进行记录。

dart @override void paint(Canvas canvas, Size size) { canvas.translate(size.width / 2, size.height / 2); int count = 3; double radius = 140 / 2; List<Offset> points = []; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; points.add(Offset(radius * cos(perRad), radius * sin(perRad))); } _drawShape(canvas, points); }

---

得到点集之后，就可以形成路径进行绘制。本例全部源码位于: 01_triangle

```dart final Paint shapePaint = Paint() ..style = PaintingStyle.stroke;

void _drawShape(Canvas canvas, List points) { Path shapePath = Path(); shapePath.moveTo(points[0].dx, points[0].dy); for (int i = 1; i < points.length; i++) { shapePath.lineTo(points[i].dx, points[i].dy); } shapePath.close(); canvas.drawPath(shapePath, shapePaint); } ```

---

2. 正 N 边形

和 正三角形 同理，改变上面的 count 值，就可以将圆等分成 count 份，再对圆上对应点进行收集即可。

| 正四边形 | 正五边形 | | ---- | ---- | | | | | 正六边形 | 正七边形 | | | |

可能大家会觉得上面奇数情况下，不是很正。因为上面以水平方向的 0° 为起点，是上下对称。视觉上，我们更习惯于 左右对称。想实现如下的左右对称 的正 N 边形，其实也很简单，在计算点位时逆时针旋转 90°即可。

dart double rotate = - pi / 2; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; points.add(Offset( radius * cos(perRad + rotate), // 在计算时加上旋转量 radius * sin(perRad + rotate), )); }

另外，通过圆的半径大小可以控制 正 N 边形 的大小。本例全部源码位于: 02nside

---

二、 N 角星的绘制

1、五角星的绘制

先看下思路：前面我们已经知道如何收录 正五边形 的五个点，现在再搞个小的 正五边形 。如果将两个点集进行交错合并，实现首尾相连会是什么样子呢？也就是 红0--蓝0--红1--蓝1--红2--蓝2...

这里外圆的五个点集为 outPoints，内圆的五个点集为 innerPoints 。让两个列表交错合并也非常简单，就是指定索引插入元素而已。

dart for(int i =0; i< count; i++){ outPoints.insert(2*i+1, innerPoints[i]); }

这样将合并的点集形成路径，就可以得到如下的图形：

---

上面图形已经有点 五角星 的外貌了，可以看出只要在收集内圆上点时，顺时针偏转一下角度就行了。比如下面偏转了 15° ，看起来就更像了：

dart double innerRadius = 70 / 2; List<Offset> innerPoints = []; double offset = 15 * pi / 180; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; innerPoints.add(Offset( innerRadius * cos(perRad + offset), innerRadius * sin(perRad + offset), )); }

---

那这个偏角到底是多少，才符合五角星呢？也就是求下面的 α 值是多少，由于小圆上五个点是 正五边形，所以 β 是 180°*(5-2)/5=108° ，所以 α = 180°-108°/2-90°=36°。

这样就得到了一个标准的五角星，只不过是上下对称的。

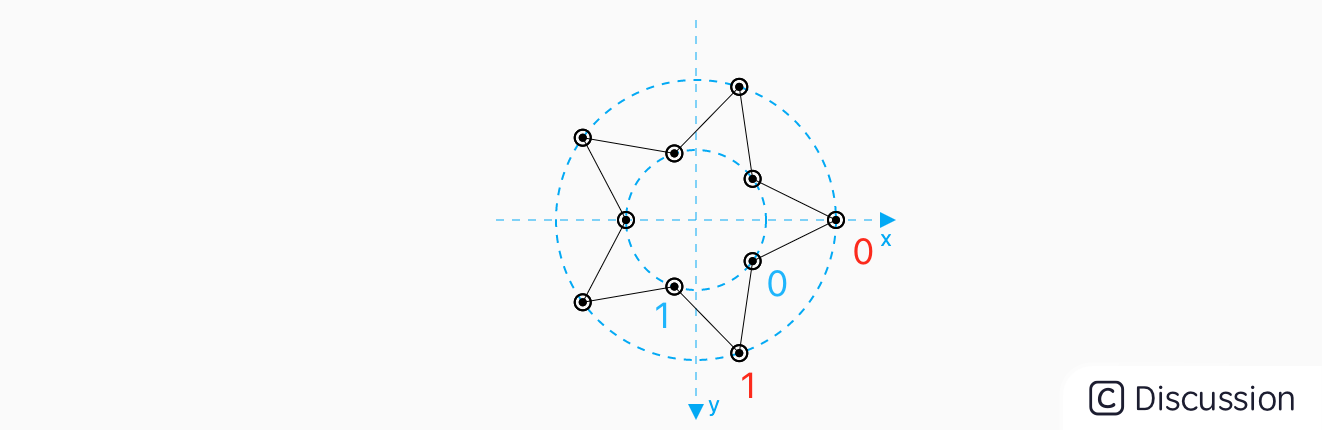
要改成左右对称 很简单，上面也说过，在计算点位时，逆时针旋转 90° 即可：本例全部源码位于: 03fivestar

dart List<Offset> innerPoints = []; double offset = pi / count; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; innerPoints.add(Offset( innerRadius * cos(perRad + rotate + offset), innerRadius * sin(perRad + rotate + offset), )); }

通过 外圆半径/内圆半径 可以控制五角星的 胖瘦 ：

| 70/40 | 70/28 | 70/15 | | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ | | | | |

---

2. N 角星的绘制

五角星完成了，其它的也就水到渠成。最重要的一步是找到角度偏移量 α 和 n 的对应关系，不难算出：

```dart α = 180°- 180°*(n-2)/n/2-90° = 180°/n

注: n 边形的内角和为 180°*(n-2) ```

上面为了方便理解，使用了两个点集分别收集内外圆上的点，最后进行整合。理解原理后，我们可以一次性收集两个圆上的点，避免而外的合并操作。代码如下：

```dart int count = 6; double outRadius = 140 / 2; double innerRadius = 70 / 2; double offset = pi / count; List outPoints = [];

double rotate = -pi / 2; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; outPoints.add(Offset( outRadius * cos(perRad + rotate), outRadius * sin(perRad + rotate), )); outPoints.add(Offset( innerRadius * cos(perRad + rotate + offset), innerRadius * sin(perRad + rotate + offset), )); } ```

---

这样，对于不同的 count ，就可以得到对应角数的星星。如下是 2~9 角星：

---

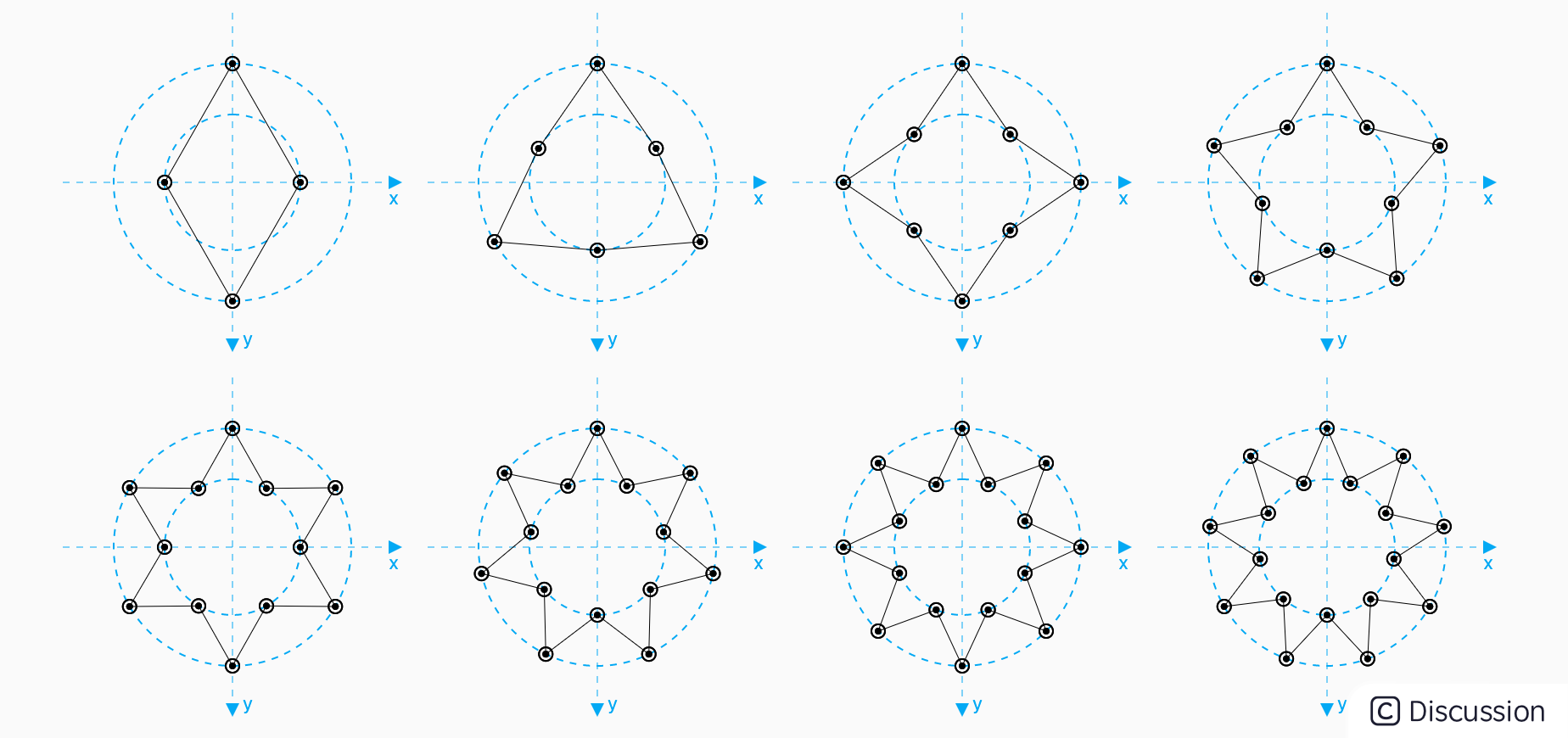
三、形状路径的使用

1、路径工具的使用

上面把所有的计算逻辑都塞在了画板中，显得非常杂乱，完全可以把这些路径形成逻辑单独抽离出来。如下 ShapePath 类，使用者只需要进行 基本参数配置 来创建对象即可，通过对象来拿到相关路径。本例全部源码位于: 04nstar

```dart // ShapePath型 成员变量 late ShapePath shapePath = ShapePath.star( n: n, outRadius: 140 / 2, innerRadius: 80 / 2, );

// 获取 shapePath 中的路径 canvas.drawPath(shapePath.path, shapePaint); ```

只需要两行代码，就可以通过ShapePath.star 构造，获得 n 角星的路径：

---

也通过ShapePath.polygon 构造，获得正 n 边形的路径：

---

2、路径工具的封装

ShapePath 中有四个成员，其中 n、outRadius 、innerRadius 是路径信息的配置，_path 是路径。在获取路径时做了个判断：如果路径为空，则先通过之前的逻辑构建路径，否则，直接返回已有路径。这样可以避免同一 ShapePath 对象构建多次相同的路径。

```dart import 'dart:math'; import 'dart:ui';

class ShapePath {

ShapePath.star({ this.n = 5, this.outRadius = 100, this.innerRadius = 60, });

ShapePath.polygon({ this.n = 5, this.outRadius = 100, }) : innerRadius = null;

final int n; final double outRadius; final double? innerRadius; Path? _path;

Path get path { if (_path == null) { _buildPath(); } return _path!; }

void _buildPath() { int count = n; double offset = pi / count; List points = []; double rotate = -pi / 2; for (int i = 0; i < count; i++) { double perRad = 2 * pi / count * i; points.add(Offset( outRadius * cos(perRad + rotate), outRadius * sin(perRad + rotate), )); if (innerRadius != null) { points.add(Offset( innerRadius! * cos(perRad + rotate + offset), innerRadius! * sin(perRad + rotate + offset), )); } }

_path = Path();
_path!.moveTo(points[0].dx, points[0].dy);
for (int i = 1; i < points.length; i++) {
  _path!.lineTo(points[i].dx, points[i].dy);
}
_path!.close();

} } ```

---

3、路径的作用

路径是绘制操作的基石，它的作用可以说非常多，可以根据路径进行合并、裁剪、描边、填充、运动等。如下是自定义 ShapeBorder 形状进行裁剪：

dart ClipPath( clipper: ShapeBorderClipper(shape: MyShapeBorder()), child: Image.asset( 'assets/images/wy_300x200.webp', height: 200, )),

```dart class MyShapeBorder extends ShapeBorder{

@override EdgeInsetsGeometry get dimensions => const EdgeInsets.all(0);

@override Path getInnerPath(Rect rect, {TextDirection? textDirection}) { return Path(); }

@override Path getOuterPath(Rect rect, {TextDirection? textDirection}) { ShapePath shapePath = ShapePath.polygon( n: 6, outRadius: rect.shortestSide/2, ); return shapePath.path.shift(Offset(rect.longestSide/2,rect.shortestSide/2)); }

@override void paint(Canvas canvas, Rect rect, {TextDirection? textDirection}) { }

@override ShapeBorder scale(double t) { return this; } } ```

路径的使用方式在 《Flutter 绘制指南 - 妙笔生花》相关章节有具体介绍，本文主要目的是来探讨：根据圆来拾取几何图形、并形成路径的方法。到这里，本文要介绍的内容就结束了，谢谢观看~