- 1创建文件并设置NTFS权限_zip64 ntfs:encrypt descriptor
- 2Unity3D - 使用天空盒子(Using Skyboxes)_unity 天空盒带远景
- 3如何拉取Gitee / GitHub上的Unity项目并成功运行_unity gitee
- 412306抢票软件 python抢票脚本_抢票软件csdn
- 5无忧秘书智脑实时互动数字人软件源码_数字人 源码 下载
- 6Android系统开发-添加USB转串口设备驱动i.MX8M开发_android usb转串口
- 7Android调试笔记——操作数据库,调用createStatement方法报空指针错误_createstatement报错
- 8Pixhawk地面站搭建问题
- 9帝国CMS十合一源码/字典/成语/古诗词/二十四节气/英语单词/百家姓/范文文库/词语等_10合一字典词典 源码
- 10vivado和modelsim 联合仿真,修改vivado中代码不重启modelsim,进行仿真_xil_defaultlib.integer
第十五届蓝桥杯省赛第二场C/C++B组F题【狡兔k窟】题解(AC)
赞
踩




题意分析
有一个 n n n 个点, n − 1 n-1 n−1 条边的无向图,边权均为 1 1 1。
每个点隶属于一个集合,同一个集合的点可以互相传送。
给定 m m m 个询问,求 x , y x, y x,y 的最短距离。
最短路解法
步骤:
- 建图。
- 对于所有询问各跑一次最短路算法。
可选用的最短路算法:
- Spfa,单次时间复杂度 O ( n ) ∼ O ( n 2 ) O(n) \sim O(n^2) O(n)∼O(n2),总时间复杂度 O ( n 2 ) ∼ O ( n 3 ) O(n^2) \sim O(n^3) O(n2)∼O(n3)。
- Dijkstra,单词时间复杂度 O ( n log n ) O(n\log n) O(nlogn),总时间复杂度 O ( n 2 log n ) O(n^2\log n) O(n2logn)。
01 BFS 解法
观察发现,本题仅存在边权为
0
0
0 和
1
1
1 的边,故上述最短路算法存在多余开销,我们考虑使用 BFS 算法进行求解,并使用 deque 进行维护。
进行扩展时,若是边权为 0 0 0 的边,则放入队头,反之放入队尾。
最坏时,每条边均扩展 n n n 个点,单次时间复杂度 O ( n 2 ) O(n^2) O(n2),总时间复杂度 O ( n 3 ) O(n^3) O(n3)。
BFS 解法
样例如下:
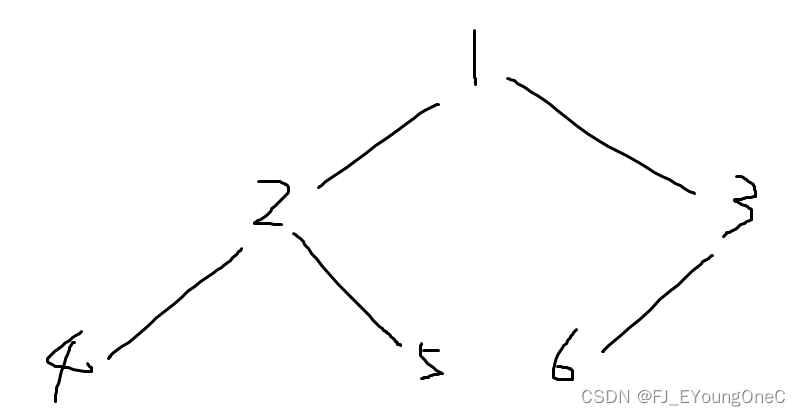
我们用虚线表示同一个组别中的连线。
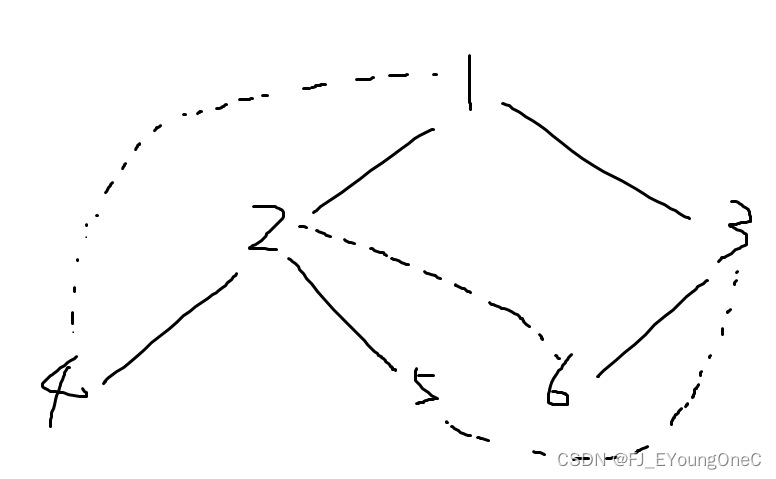
合并 1 , 4 1, 4 1,4:

合并
2
,
6
2, 6
2,6:
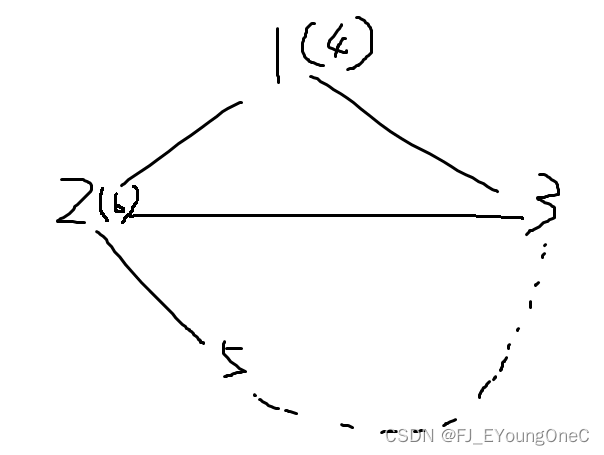
合并
3
,
5
3, 5
3,5:
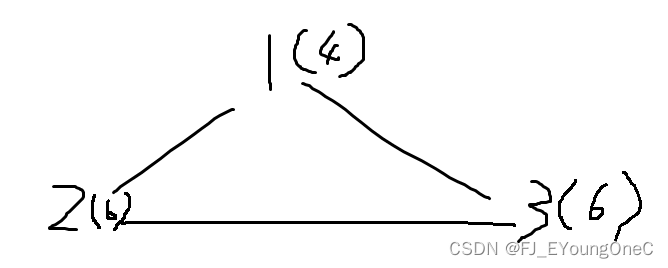
那么,在合并之后,当我们要算两个点之间的最短距离时,可以直接用 BFS 算法解决。
观察上图发现,因为组别内的点的边权为 0 0 0,所以我们可以将所有同一个组别的点进行合并,将点于点之间的最短路转换为组别于组别之间的最短路。
单词时间复杂度 O ( n ) O(n) O(n),总时间复杂度 O ( n 2 ) O(n^2) O(n2)。
#include <iostream> #include <cstring> #include <algorithm> #include <cstdio> #include <queue> #include <vector> using namespace std; const int N = 5e3 + 10, M = N * 4; int n, m; int h[N], e[M], w[M], ne[M], idx; int belong[N]; vector<int> g[N]; int dist[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++; } void bfs(int u, int v) { memset(dist, 0x3f, sizeof dist); memset(st, 0, sizeof st); dist[u] = 0; queue<int> q; q.push(u); while (q.size()) { auto t = q.front(); q.pop(); for (int i = h[t]; ~i; i = ne[i] ) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; q.push(j); } } } cout << dist[v] << endl; } int main() { ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin >> n >> m; memset(h, -1, sizeof h); for (int i = 1; i <= n; ++ i ) { int x; cin >> x; belong[i] = x; g[x].push_back(i); } for (int i = 1; i < n; ++ i ) { int a, b; cin >> a >> b; a = belong[a], b = belong[b]; add(a, b, 1), add(b, a, 1); } while (m -- ) { int a, b; cin >> a >> b; bfs(belong[a], belong[b]); } return 0; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86




