【算法】【树状数组】 原理详解、模板与例题_树状数组算法

树状数组要解决什么问题

m次操作，每次操作可以查询数组区间长度为n的 和/积，或者更新某位置的值。

不用树状数组的几种处理方式：

• 每次查询直接扫描该区间取和，一次取和时间复杂度为O(n)。更新时间复杂度为O(1)
• dp思想提前获取前缀和数组，每次取和直接取区间结尾前缀和减区间开头前缀和的值，这样时间复杂度为O(1)，但是更新时需要从更新位置更新前缀和数组，时间复杂度为O(n)
• 线段树算法，树状数组能解决的线段树都能解决，但是线段树代码量较大，容易出错。取和和更新的时间复杂度都为O(logn)

树状数组取和和更新的时间复杂度都为O(logn)

树状数组的逻辑

下图为建立树状数组的过程及查询、更新的逻辑。本文以求区间和为例。

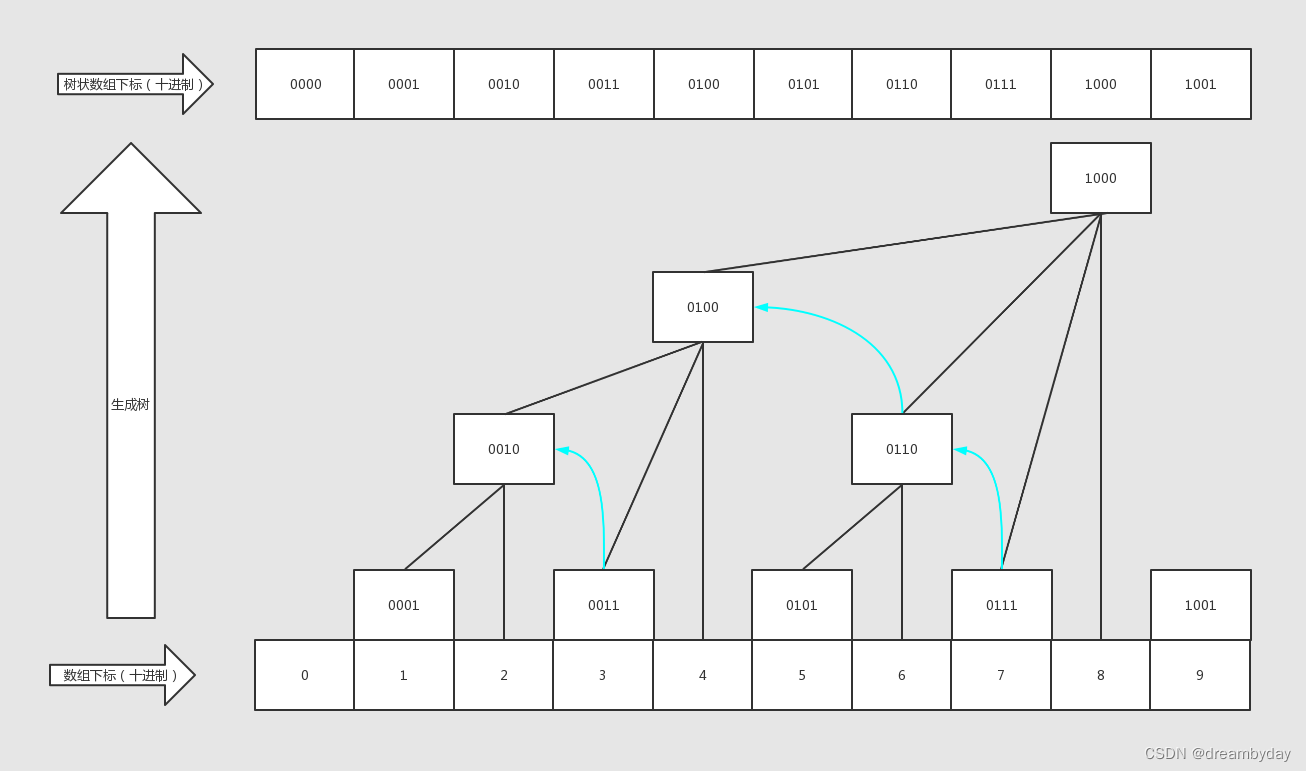
tree代表树状数组，arr代表原数组

如图，树状数组每个位置存储一段区间和。如
tree[1]=arr[1]
tree[2]=arr[1]+arr[2]
tree[3]=arr[3]
tree[4]=arr[1]+arr[2]+arr[3]+arr[4]

如何查询区间和

求区间[4,7]的和，则是求出[1,7]的和-[1,3]的和

流程

树状数组的特点是：树状数组的下标为管辖区间的结尾。求和需要将自己及之前的所有区间和相加，因此需要不断找上个区间。

图中蓝线是找上个区间的含义，

• tree[7]+tree[6]+tree[4]得到区间[1,7]的和
• tree[3]+tree[2]得到区间[1,3]的和

两者相减即为[4,7]和

如何查找上个区间树状数组的下标

位运算lowbit

由该数值二进制计算出只包含二进制结尾1的数值。计算方式是 m&(-m)。

7(0111)->7(0111)&-7(0001)->1(0001)
6(0110)->6(0110)&-6(0010)->2(0010)
查找上个位置

m-lowbit(m)=>m-m&(-m)

7->7-1->6
6->6-2->4
4->4-4->0

累计求和

不断找上个位置，直到位置0。累计加和即为结果

如何更新

如arr[1]的值从3变成7，相当于其结果增加了4，则依次更新树状数组的节点及父节点。

tree[1]->tree[1]+4
tree[2]->tree[2]+4
tree[4]->tree[4]+4
tree[8]->tree[8]+4

更新直至超出数组范围。

初始如何建树状数组

遍历原始数组，相当于每次对树状数组的值进行更新（数组初始元素为0）

模板代码

树状数组的工具类

/**
     * 下标从0开始的树状数组
     */
    class BIT {
        // 根据原始数组生成树状数组
        int[] treeArray;
        // 原始数组
        int[] originalArray;

        /**
         * 构造方法，
         * @param originalArray 原始数组
         */
        public BIT(int[] originalArray) {
            // 初始化树状数组
            treeArray = new int[originalArray.length];
            // 复制原始数组
            this.originalArray = Arrays.copyOf(originalArray,originalArray.length);
            // 构造树状数组，遍历原始数组，对树状数组每个位置更新
            for (int i = 0; i < originalArray.length; i++) {
                add(i, originalArray[i]);
            }
        }

        /**
         * 取x+1值的二进制最后一个1
         * 这里加一是为了能够使用下标从0开始的原始数组。
         * @param x 原始数组下标
         * @return 最后一个1代表的数值
         */
        private int lowBit(int x) {
            x++;
            return x & (-x);
        }

        /**
         * 查询区间[0,endPosition]的和
         * @param endPosition 结束位置
         * @return 取和
         */
        public int query(int endPosition) {
            // 查询范围小于0直接返回0
            if (endPosition < 0) {
                return 0;
            }
            int res = 0;
            // 从前往后找，将每段区间和相加
            while (endPosition >= 0) {
                res += treeArray[endPosition];
                // 计算存储上一个区间和的元素下标
                endPosition = endPosition - lowBit(endPosition);
            }
            return res;
        }

        /**
         * 原始数组某位置增加数值，更新树状数组
         * @param position 位置
         * @param value 增加的值
         */
        private void add(int position, int value) {
            while (position < treeArray.length) {
                treeArray[position] += value;
                position = position + lowBit(position);
            }
            originalArray[position] = value;
        }

        /**
         * 原始数组某位置修改数值，更新树状数组
         * @param position 位置
         * @param value 修改的值
         */
        public void set(int position, int value) {
            int diff = value - originalArray[position];
            add(position, diff);
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

使用例子

	private BIT bit;
	// 初始化
    public NumArray(int[] nums) {
        bit = new BIT(nums);
    }
	// 更新某位置值
    public void update(int index, int val) {
        bit.set(index,val);
    }
	// 取区间和
    public int sumRange(int left, int right) {
        return bit.query(right) - bit.query(left - 1);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

例题

• 307. 区域和检索 - 数组可修改
• POJ3468

---

17年写的C++代码，留个纪念
POJ3468

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<cmath>
#include<set>
#include<vector>
#include<map>
#include<string>
#include<stdlib.h>
#include<limits.h>
using namespace std;
/******************************************************/
#define LL long long int
#define mem(a,b) memset(a,b,sizeof(a))
#define m ((l+r)/2)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define L rt<<1
#define R rt<<1|1
#define N 400000+1
#define pow(a) a*a
#define INF 0x3f3f3f3f
#define max(a,b) (a>b?a:b)
#define min(a,b) (a<b?a:b)
#define lowbit(x) (x&-x)
/*********************************************************/
/*sum[x] = org[1]+...+org[x] + delta[1]*x +
delta[2]*(x-1) + delta[3]*(x-2)+...+delta[x]*1
= org[1]+...+org[x] + segma(delta[i]*(x+1-i))
= segma(org[i]) + (x+1)*segma(delta[i]) - segma(delta[i]*i)，1 <= i <= x*/
/***************************************************/
/*10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4*/
LL n, q;
LL dat[N];
LL summ[N];
LL bit0[N], bit1[N];
char s[2];
void add(LL arr[],LL x, LL d){
	while (x <= n){
		arr[x] += d;
		x += lowbit(x);
	}
}
LL find(LL x,LL su[]){
	LL res = 0;
	while (x > 0){
		res += su[x];
		x -= lowbit(x);
	}
	return res;
}
int main(){
	mem(summ, 0);
	mem(bit0, 0);
	mem(bit1, 0);
	scanf("%lld%lld", &n, &q);
	for (int i = 1; i <= n; i++)scanf("%lld", &dat[i]);
	summ[0] = 0;
	for (int i = 1; i <= n; i++){
		summ[i] = summ[i - 1] + dat[i];
	}
	while (q--){
		LL a, b;
		scanf("%s%lld%lld", s, &a, &b);
		if (s[0] == 'Q'){
			LL sum = summ[b] - summ[a - 1];
			LL sum1 =(b+1)* find(b, bit0) - find(b, bit1);
			LL sum2 = a*(find(a - 1, bit0)) - find(a - 1, bit1);
			printf("%lld\n", sum + sum1 - sum2);
		}
		else{
			LL c; scanf("%lld", &c);
			add(bit0, a, c);
			add(bit0, b + 1, -c);
			add(bit1, a, c*a);
			add(bit1, b + 1, -c*(b + 1));
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85