【PID】PID的调整方法_pid三个参数的调整方法

一.PID介绍

PID控制器是通过对误差信号e(t)进行比例，积分和微分运算，其结果的加权，得到控制器的输出U(t)，该值就是控制对象的控制值。
PID控制器的数学描述为:

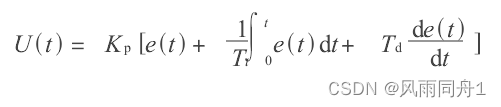
其中的:e(t)=r(t)-c(t)为误差信号。r(t)为输入量；c(t)为输出量；U(t)为控制器的输出；Kp为控制器的比例放大系数；TI为控制器的积分时间常数；Td为控制器的微分时间常数。

二.PID参数介绍

1. 比例系数Kp

比例系数增加时，系统的响应速度会加快，系统的稳态误差则会降低。从而能够提高控制精度。
当比例系数Kp过大，会使系统出现超调量，导致系统发生振荡或使振荡次数增加，以至于系统的稳定性变低，反而延长了调节时间。
当比例系数Kp过小，系统调节将会变得缓慢。

2. 积分时间常数Ki

积分时间常数Ki主要对积分作用的强弱产生影响，其值越小作用越强。
当积分时间常数Ki过大，系统虽然在一定程度上减小了超调量和振荡，但是也会增加系统为了消除静差所消耗的时间。
当积分时间常数Ki过小，便会引起振荡次数增加，导致系统稳定性变差。

3. 微分时间常数Kd

微分时间常数Kd对系统的稳态过程不存在影响，仅在其动态过程中起作用。其值偏大或偏小都会引起系统的超调量的增大，延长调节时间，因此合理的Kd值才能获得比较满意的过渡过程。

三.PID的调整方法

1.响应缓慢，可增大Kp

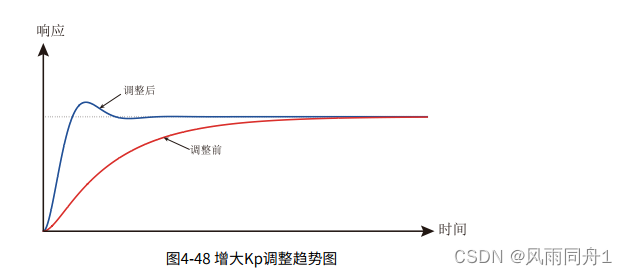
增大Kp调整趋势图

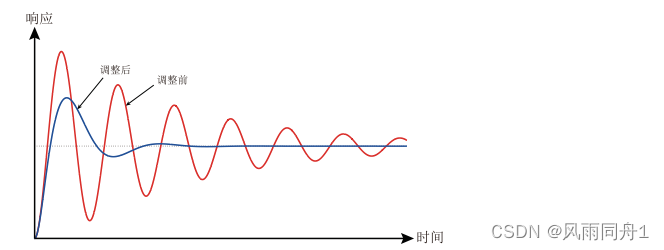
２.快速震荡，可减小Kp

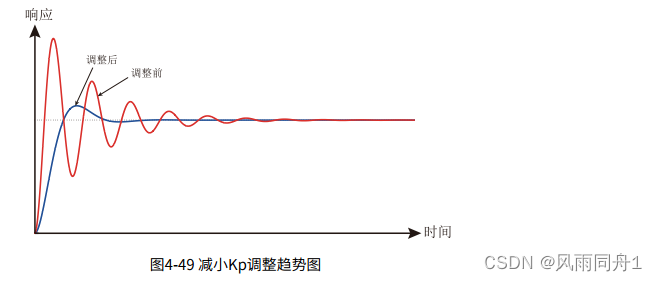
减小Kp调整趋势图

3.超调大，波动慢，可增大Ti

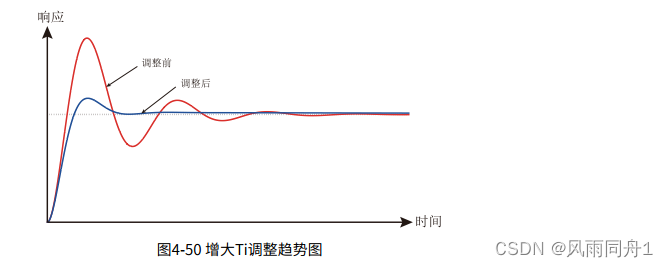
增大Ti调整趋势图

4.负载波动时，静差大，回复慢，可增大Kp或减小Ti

负载波动时，增大Kp调整趋势图

负载波动时，减小Ti调整趋势图

5.加入适量的微分时间Td，可改善系统的稳定性(避免加入过大引入干扰和振荡)