二刷算法训练营Day41 (Day40休息) | 动态规划(3/17)

目录

详细布置：

1. 背包问题理论基础

1.1 01背包

2. 46. 携带研究材料（第六期模拟笔试）

一维dp数组（滚动数组）

3. 416. 分割等和子集

---

详细布置：

1. 背包问题理论基础

但说实话，背包九讲对于小白来说确实不太友好，看起来还是有点费劲的，而且都是伪代码理解起来也吃力。

对于面试的话，其实掌握01背包，和完全背包，就够用了，最多可以再来一个多重背包。

如果这几种背包，分不清，我这里画了一个图，如下：

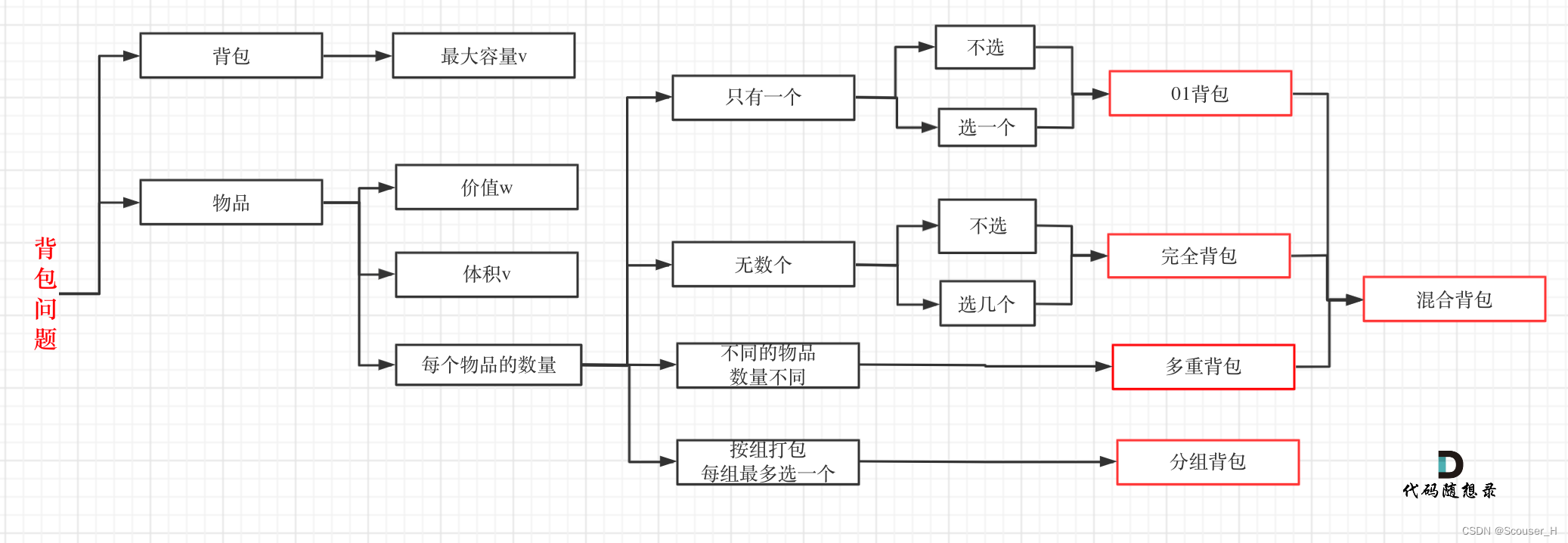
至于背包九讲其他背包，面试几乎不会问，都是竞赛级别的了，leetcode上连多重背包的题目都没有，所以题库也告诉我们，01背包和完全背包就够用了。

而完全背包又是也是01背包稍作变化而来，即：完全背包的物品数量是无限的。

所以背包问题的理论基础重中之重是01背包，一定要理解透！

leetcode上没有纯01背包的问题，都是01背包应用方面的题目，也就是需要转化为01背包问题。

所以我先通过纯01背包问题，把01背包原理讲清楚，后续再讲解leetcode题目的时候，重点就是讲解如何转化为01背包问题了。

1.1 01背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

def test_2_wei_bag_problem1():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagweight = 4
 
    # 二维数组
    dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
 
    # 初始化
    for j in range(weight[0], bagweight + 1):
        dp[0][j] = value[0]
 
    # weight数组的大小就是物品个数
    for i in range(1, len(weight)):  # 遍历物品
        for j in range(bagweight + 1):  # 遍历背包容量
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
 
    print(dp[len(weight) - 1][bagweight])
 
test_2_wei_bag_problem1()

---

2. 46. 携带研究材料（第六期模拟笔试）

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的空间，并且具有不同的价值。 

小明的行李空间为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料只能选择一次，并且只有选与不选两种选择，不能进行切割。

一维dp数组（滚动数组）

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了，i是物品，j是背包容量。

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

一定要时刻记住这里i和j的含义，要不然很容易看懵了。

def test_1_wei_bag_problem():
    weight = [1, 3, 4]
    value = [15, 20, 30]
    bagWeight = 4
 
    # 初始化
    dp = [0] * (bagWeight + 1)
    for i in range(len(weight)):  # 遍历物品
        for j in range(bagWeight, weight[i] - 1, -1):  # 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
 
    print(dp[bagWeight])
 
 
test_1_wei_bag_problem()

---

3. 416. 分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。

要注意题目描述中商品是不是可以重复放入。

即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法还是不一样的。

要明确本题中我们要使用的是01背包，因为元素我们只能用一次。

回归主题：首先，本题要求集合里能否出现总和为 sum / 2 的子集。

那么来一一对应一下本题，看看背包问题如何来解决。

只有确定了如下四点，才能把01背包问题套到本题上来。

• 背包的体积为sum / 2
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入。

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        
        total_sum = sum(nums)
 
        if total_sum % 2 != 0:
            return False
 
        target_sum = total_sum // 2
        dp = [[False] * (target_sum + 1) for _ in range(len(nums) + 1)]
 
        # 初始化第一行（空子集可以得到和为0）
        for i in range(len(nums) + 1):
            dp[i][0] = True
 
        for i in range(1, len(nums) + 1):
            for j in range(1, target_sum + 1):
                if j < nums[i - 1]:
                    # 当前数字大于目标和时，无法使用该数字
                    dp[i][j] = dp[i - 1][j]
                else:
                    # 当前数字小于等于目标和时，可以选择使用或不使用该数字
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]
 
        return dp[len(nums)][target_sum]