[计算机图形学入门]9.几何_catmull-clark subdivision算法是几何算法吗

目录

一.隐式几何

1.隐函数(一个简单的理解)

 2.隐式几何

 3.一些隐式的几何表示法

 二.显式几何

1.显函数(一个简单的理解)

 2.显式几何

3.一些显示表示的几何

三.曲线  --显示几何表示方法

1.贝塞尔曲线

 2.样条曲线

四.曲面

1.贝塞尔曲面

 2.网格表示曲面

五.曲面细分

1.Loop Subdivision用于细分三角形

 2.Catmull-Clark Subdivision

六.曲面简化

1.边坍缩

---

一.隐式几何

1.隐函数(一个简单的理解)

 2.隐式几何

用隐函数表示的集合,表示将一堆点归类.给一组坐标,隐式表示能看直接看出是否在几何表面.但若要找哪些点在隐式几何上,相对较难.

 3.一些隐式的几何表示法

①.数学公式表示,不适合复杂几何

 ②.CSG,对几何做布尔运算

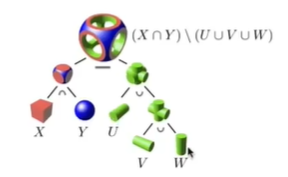
③.距离函数

 用某一点到几何表面最近距离的函数来表示几何.

图例是将两个几个的距离函数blend融合后,在恢复成原来的样子所得到的.

适合几何间圆滑的过渡.

 应用距离函数的例子:

 把混合后的距离函数,值为0的地方全找出来,就可以恢复物体表面.

 -水平集表述法恢复几何

类似地理等高线,找到函数值相同的多个点.

 ④.分形几何

类似递归

 二.显式几何

1.显函数(一个简单的理解)

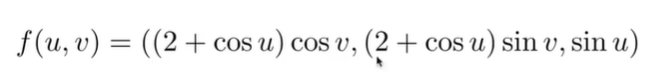
 2.显式几何

能很快知道有哪些点在平面上,但难判断一个点是不是在平面上.

3.一些显示表示的几何

①.点云(不常用)

将物体表面由无数个点表示,list if points(x,y,z)

 点云之后会被变成多边形的面.

 ②.多边形面(常用)

 obj文件:

三.曲线  --显示几何表示方法

1.贝塞尔曲线

用一系列的控制点来定义曲线.

曲线起始方向p1p0,结束方向p3p2. 曲线不一定要经过控制点.

. ①.如何用控制点画出贝塞尔曲线

-几何理解

        -三个控制点的二次贝塞尔曲线

         -四个控制点

 -代数理解

b01 = (1-t)b0 + tb1,t==0时,b01==b0

接着递归,继续插值(第一张图t与1-t反了)

 下图资料来源计算机图形学十：几何2—贝塞尔曲线(Bézier Curves)与贝塞尔曲面(Bézier Surfaces)

 贝塞尔曲线不一定要在平面内,空间上也可以.

 -贝塞尔曲线性质:

t==0一定在起点,t==1一定在终点.一定过起点终点与初末控制点连线的切线.

贝塞尔曲线若要仿射变换,则对控制点仿射变换,再画出曲线即可.但还是不满足投影不变.

贝塞尔曲线一定在控制点围成的凸包内

②.逐段贝塞尔曲线

当控制点数量多时,控制效果并不好

 则引入逐段贝塞尔曲线,对于长曲线,可以分为一个控制点一组来控制一段曲线,最后将多段曲线拼接.拼接处若切线方向共线则可以平滑拼接.

 拼接点位置相同叫c0连续,若切线共线叫c1连续.

 2.样条曲线

 -B-样条

        -基函数

        -具有局部性,不会一点动,曲线全动.

四.曲面

1.贝塞尔曲面

在两个反向分别用贝塞尔曲线

 不断扫描,变成一个面.

 2.网格表示曲面

根据需要选择合适的几何表述方法. 

五.曲面细分

-分出更多三角形 -三角形位置发生变化

细分方法:

1.Loop Subdivision用于细分三角形

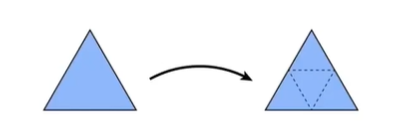
 一个三角形被拆成了四个.

分出新老顶点,分别进行不同操作.

如果更新新的顶点的位置?

对于某新点(白色),用右边的加权平均来更新位置

 对于某旧点(图中白点),用公式更新位置.

公式: pos = (1-n*u)original_pos + u * neighbor_pos_sum(相邻旧点的位置和)

n为顶点的度(出度入度的度),若n=3,u=3/16,否则u=3/(8n).

 2.Catmull-Clark Subdivision

对于非三角形面的细分.

先定义一些概念:非四边形面,奇异点(度不为四的点).

 取非四边形面边上的中点,与非四边形面中点连接.这之后,奇异点增加了2(与之前的非四边形面的数量有关),非四边形面消失了.就好像非四边形面在细分后变成了奇异点.之后的细分不会再增加奇异点数了.

 关于点的位置更新公式:

新面中的点,新边中的点,老的点(按顺序对于图中公式)

 两种细分对比:

六.曲面简化

提高程序性能

如何简化?

1.边坍缩

将多个顶点捏在一起合成一个新顶点

-二次误差度量Quadric Error Metrics

        使简化后的模型能最大程度还原原本的模型.

        找到点的一个最优位置,使其到原本平面距离平方和最小

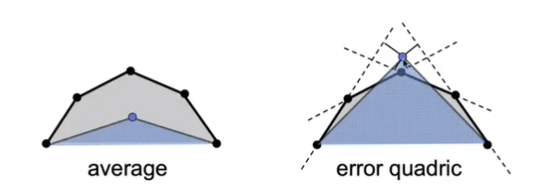
         可以对于每一条边,坍缩后选二次误差度量小的边坍缩.利用到堆数据结构,选取最小,更新堆结构,再取...(贪心算法)

资料来源Games101